План
- Прямоугольный базис в пространстве.
- Координаты точки и вектора в пространстве.
3. Разложение вектора по трём некомпланарным направлениям
- Действия с векторами в координатной форме
Вопрос 1. Прямоугольный базис в пространстве.
Для построения прямоугольного базиса в пространстве нужно:
- провести три взаимно перпендикулярных прямые х, у, z, пересекающихся в одной точке О;
- провести через каждую пару этих прямых плоскость.
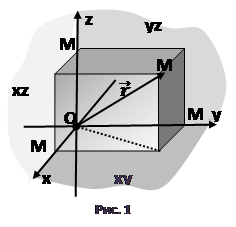 Плоскость, проходящая через прямые х и у, называют плоскостью ху, две другие плоскости соответственно хz и уz.
Плоскость, проходящая через прямые х и у, называют плоскостью ху, две другие плоскости соответственно хz и уz.
Прямые х, у, z называются координатными осями, х – ось абсцисс, у – ось ординат, z – ось аппликат. Точка пересечения О – начало координат, плоскости ху, хz, уz – координатные плоскости. Точка О разбивает каждую из этих осей на две полуоси, одна из которых положительная, а другая отрицательная (рис. 1).
Пусть 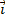 – единичный вектор оси абсцисс,
– единичный вектор оси абсцисс,  - единичный вектор оси ординат,
- единичный вектор оси ординат,  - единичный вектор оси аппликат.
- единичный вектор оси аппликат.

Тройка взаимно перпендикулярных, единичных векторов (i, j, k), отложенных от начала координат точки О и по направлению совпадающих с координатными осями, называют прямоугольным базисом в пространстве (рис. 2).
|
 Вопрос 2. Координаты точки и вектора в пространстве.
Вопрос 2. Координаты точки и вектора в пространстве.
Любая точка М(x; y; z) в пространстве имеет 3 координаты: х- абсцисса, у- ордината, z- аппликата (рис. 3).
Любой вектор  ={х; у; z} или
={х; у; z} или  { х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:
{ х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:
х- абсцисса, у- ордината, z- аппликата.
|
Радиус-вектором называют вектор, проведённый из начала координат в произвольную точку пространства.Радиус-вектор имеет координаты точки, в которую он проведён (рис. 4).
|
|
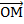 =
=  ={х; у; z}
={х; у; z}
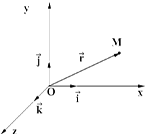 Координаты вектора
Координаты вектора 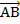 выражаются через координаты его начала А(х 1; у 1; z 1) и конца В(х 2; у 2; z 2):
выражаются через координаты его начала А(х 1; у 1; z 1) и конца В(х 2; у 2; z 2):
 { х2 – х1, у2 – у1, z2 – z1}.
{ х2 – х1, у2 – у1, z2 – z1}.
Правило 1. Для определения координат вектора АВ нужно от координат конца вектора вычесть координаты начала.
|
Вопрос 3. Разложение вектора по трём некомпланарным направлениям:
а) разложение радиус-вектора по базису
Пусть 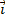 – единичный вектор оси абсцисс,
– единичный вектор оси абсцисс,  - единичный вектор оси ординат,
- единичный вектор оси ординат,  - единичный вектор оси аппликат. Радиус-вектор
- единичный вектор оси аппликат. Радиус-вектор 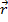 =
= 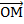 можно разложить по единичным векторам:
можно разложить по единичным векторам:
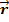 = x
= x 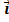 + y
+ y  + z
+ z 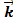 .
.
Коэффициенты х, у, z называются координатами вектора 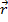 ={х; у; z}: х = ОМх, у = ОМу, z = ОМz.
={х; у; z}: х = ОМх, у = ОМу, z = ОМz.
б) разложение произвольного вектора АВ по базису
 (х2 – х1)i+(у2 – у1)j+(z2 – z1)k.
(х2 – х1)i+(у2 – у1)j+(z2 – z1)k.
Правило 2. Для разложения вектора по базису нужно каждую координату вектора умножить на соответствующий координатный (базисный) вектор.
Вопрос 4. Действия с векторами в координатной форме:
Правило 3. Суммой (разностью) векторов 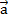 (х1; у1; z1) и
(х1; у1; z1) и 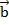 (х2; у2; z2) называется вектор
(х2; у2; z2) называется вектор 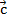 =
= 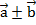 , координаты которого равны сумме (разности) соответствующих координат этих векторов:
, координаты которого равны сумме (разности) соответствующих координат этих векторов:
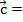 (х1
(х1 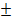 х2; у1
х2; у1 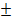 у2; z1
у2; z1 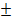 z2).
z2).
Правило 4. Произведением вектора  (х; у; z) на число k называется вектор
(х; у; z) на число k называется вектор
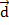 =k
=k 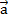 , координаты которого равны произведению числа k на координаты вектора
, координаты которого равны произведению числа k на координаты вектора 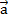 :
:
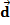 =(kх; kу; kz).
=(kх; kу; kz).
Правило 5. Построение точки в пространстве
Для построения точки в пространстве необходимо:
1) Построить прямоугольную систему координат в пространстве Охуz.
2) Отложить первые две координаты на соответствующих осях и провести их проекции;
|
|
3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

Правило 6. Построение радиус-вектора в пространстве
Для построения радиус-вектора в пространстве необходимо:
1) Построить прямоугольную систему координат в пространстве Охуz.
2) Отложить первые две координаты конца вектора на соответствующих осях и провести их проекции;
|
4) Соединить полученную точку с началом координат и обозначить искомый вектор (рис. 5).
Правило 7. Построение вектора MN впространстве
Для построения вектора MN в пространстве необходимо:
1) Построить прямоугольную систему координат в пространстве Охуz.
2) По правилу (5) построить 2 точки - точку начала вектора M(-2;0;3) и точку конца N(2;1; -2).
3) Соединить полученные точки и обозначить искомый вектор (рис. 6).

|