Кафедра естественнонаучных дисциплин имени профессора
Финкеля Виктора Моисеевича
 Отчет
Отчет
по лабораторной работе № 1 МЕХ
«__________________________________________________________________________________________________________________________________________________________________»
Выполнил ст. группы ________
____________________________
(Фамилия, инициалы)
Преподаватель
д-р. техн. наук, доцент Романов Д.А.
(Фамилия, инициалы)
 |
Содержание конспекта отчета
По лабораторной работе
(выполняется от руки или
В печатном виде на формате А5)
Титульный лист по образцу.
Цель, задачи лабораторной работы.
Приборы и принадлежности.
4. Схема или рисунок установки (с надписью и пояснением всех входящих в схему элементов), а также рисунки, поясняющие вывод рабочих формул.
Основные расчетные формулы, с обязательным пояснением величин, входящих в формулу.
Таблицы.
Примеры расчета.
Графики и диаграммы.
9. Выводы (заключение) по лабораторной работе обязателен.
Министерство образования и науки РФ
Федеральное государственное бюджетное
образовательное учреждение высшего
профессионального образования
«Сибирский государственный индустриальный университет»
Кафедра естественнонаучных дисциплин имени профессора Финкеля Виктора Моисеевича
 Отчет
Отчет
по лабораторной работе № 5 фм
«Определение скорости полета пули И ПОТЕРИ
МЕХАНИЧЕСКОЙ ЭНЕРГИИ при НЕупругом
Взаимодействии В системЕ «пуля – стержень»
На основе изучения законов сохранения
В механике»
Выполнил ст. группы ______
___________________________
(Фамилия, инициалы)
Преподаватель
____________________________
(Фамилия, инициалы)
 |
КРАТКАЯ ТЕОРИЯ
Рассмотрим физический маятник, который представляет собой твердое тело в виде стрежня массой mM .,совершающее колебания под действием силы тяжести относительно горизонтальной оси О, не проходящей через его центр масс С. В этот маятник после выстрела из пружинного пистолета попадает пуля массой mП и застревает там в пластилине на расстоянии l1 от оси вращения. Маятник с застрявшей в нем пулей может откланяться на угол a.
Скорость полета пули можно определить, пользуясь законами сохранения момента импульса и механической энергии.
Моментом импульса материальной точки 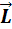 относительно точки О называется векторная величина, определяемая векторным произведением радиус – вектора
относительно точки О называется векторная величина, определяемая векторным произведением радиус – вектора  материальной точки на ее импульс
материальной точки на ее импульс  :
: 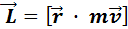 .
.
Численное значение момента импульса определяется как 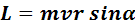 .
.
Моментом импульса тела относительно оси вращения называется величина 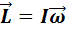 , где
, где 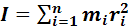 – момент инерции тела относительно оси вращения,
– момент инерции тела относительно оси вращения, 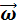 – угловая скорость вращения тела.
– угловая скорость вращения тела.
Закон сохранения момента импульса: в замкнутой системе тел момент импульса есть величина постоянная: 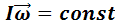 , если результирующий момент внешних сил
, если результирующий момент внешних сил  .
.
Воспользуемся законом сохранения момента импульса системы «пуля – стержень», которую можно считать замкнутой в момент удара, так как при соударении возникают большие внутренние силы взаимодействия, много превышающие внешние силы. В условиях опыта сохраняется проекция момента импульса системы на ось Z, совпадающей с направлением вектора углового перемещения стержня при его отклонении от вертикального положения
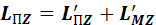 , (1)
, (1)
где 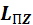 – проекция момента импульса пули до соударения с маятником;
– проекция момента импульса пули до соударения с маятником;
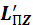 – проекция момента импульса пули сразу после соударения с маятником;
– проекция момента импульса пули сразу после соударения с маятником;
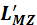 – проекция момента импульса маятника сразу после соударения с пулей.
– проекция момента импульса маятника сразу после соударения с пулей.
В уравнении (1) учтено то, что до удара стержень неподвижен. Считая пулю материальной точкой, запишем ее проекцию момента импульса:
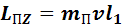 , (2)
, (2)
где mП – масса пули;
v – скорость пули до соударения с маятником;
l1 – расстояние от центра вращения до точки соударения пули с маятником.
Сразу после неупругого удара пуля вместе со стержнем будет двигаться с угловой скоростью w. Тогда сумма моментов импульса пули и стержня равна
 , (3)
, (3)
где Iм – момент инерции физического маятника;
ω – угловая скорость вращения маятника.
С учетом (2) и (3) получим уравнение для скорости пули:
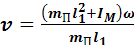 . (4)
. (4)
Пренебрегая силой сопротивления воздуха и силой трения на оси вращения стержня, определим угловую скорость сразу после удара с помощью закона сохранения механической энергии:
 , (5)
, (5)
где  – кинетическая энергия пули сразу после удара;
– кинетическая энергия пули сразу после удара;
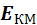
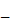 кинетическая энергия маятника сразу после удара;
кинетическая энергия маятника сразу после удара;
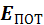 – потенциальная энергия системы «пуля-маятник» в момент максимального отклонения от вертикального положения маятника.
– потенциальная энергия системы «пуля-маятник» в момент максимального отклонения от вертикального положения маятника.
В этом выражении каждый из членов равен
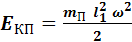 , (6)
, (6)
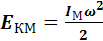 , (7)
, (7)
 , (8)
, (8)
где h – высота подъема центра масс системы в момент максимального отклонения от положения равновесия на угол a,
 – масса маятника.
– масса маятника.
Связь между углом a и h имеет вид:
 (9)
(9)
где lC – расстояние от оси вращения до центра масс маятника.
Формула (9) получена в предположении, что масса пули много меньше массы стержня, а, значит, пуля мало влияет на положение центра масс.
Подставляя (6), (7), (8), (9) в (5) получим
 . (10)
. (10)
Отсюда получим формулу угловой скорости:
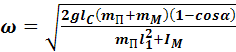 . (11)
. (11)
Подставляя (11) в (4) получаем рабочую формулу для определения скорости полета пули по углу отклонения маятника:
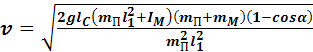 . (12)
. (12)
Учитывая кинетическую энергию пули, вылетающую из пружинного пистолета с начальной скоростью v, до удара о стержень, запишем закон сохранения энергии, а также закон сохранения момента импульса системы (1) «пуля – стержень», пренебрегая потенциальной энергией системы в момент удара
 (13)
(13)
где 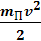 и
и  – кинетическая энергия и проекция момента импульса пули до удара о стержень,
– кинетическая энергия и проекция момента импульса пули до удара о стержень,
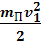 и
и 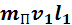 – кинетическая энергия и проекция момента импульса пули в момент удара о стержень,
– кинетическая энергия и проекция момента импульса пули в момент удара о стержень,
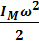 и
и 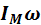 – кинетическая энергия и проекция момента импульса стержня сразу после удара пули о стержень.
– кинетическая энергия и проекция момента импульса стержня сразу после удара пули о стержень.
Из системы уравнений (13) определим потери механической энергии Q в результате неупругого удара пули о стержень:
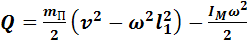 . (14)
. (14)
где IM – момент инерции маятника, определяемый по формуле (17),
v – скорость пули, определяемая по формуле (12),
ω – угловая скорость маятника, определяемая по формуле (11),
 – скорость пули в момент удара о стержень.
– скорость пули в момент удара о стержень.
ЦЕЛЬ И ЗАДАЧИ
Цель работы: на основании законов сохранения момента импульса и механической энергии определить скорость полета пули и потерю механической энергии при неупругом ударе в замкнутой системе «пуля – стержень».
Задачи работы:
1. Изучить понятие замкнутой системы, закон сохранения момента импульса и полной механической энергии при упругом и неупругом взаимодействии тел.
2. Экспериментально измерить период колебаний маятника (T) после взаимодействия с пулями разных масс.
3. Расчетным путем определить момент инерции стержня (I).
4. Определить скорость полета пули (v) и потерю механической энергии (Q) при неупругом взаимодействии тел.
5. На основе измерений угла отклонения, периода колебаний системы «пуля–маятник» и момента инерции маятника получить значение скорости полета пули и построить график зависимости в координатах «v – 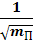 ».
».
Ход работы
1. Определяем период (T) 10 полных колебаний по формуле (1) и среднее значение периода (Tср):
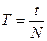 . (1)
. (1)
2. По формулам (2) и (3) рассчитаем момент инерции физического маятника:
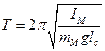 , (2)
, (2)
где mM – масса маятника,
lc – расстояние от оси вращения до центра масс маятника,
IM – момент инерции маятника, равный
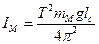 . (3)
. (3)
3. Определяем погрешности измерений времени (приборная) (Δtα) и периода колебаний (ΔTα) маятника (ошибка косвенного измерения), а также момента инерции (косвенное измерение) маятника (ΔIα) по формуле (4):
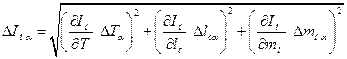 . (4)
. (4)
4. Результаты измерений заносим в таблицу 1.
Таблица 1
| φ =150; mм=(0,088±0,002)кг; lc=(0,120±0,005)м; N=10. | |||||||
| № опыта | t, c. | Δtα, c. | T, c. | Tср, c. | ΔTα, c. | Iмср, кг·м2 | ΔIмα, кг·м2 |
| 8,00 | 0,005 | 0,800 | 0,79 | 0,0005 | 1,67·10-3 | 0,08·10-3 | |
| 7,99 | 0,799 | ||||||
| 8,03 | 0,803 | ||||||
| 7,79 | 0,779 | ||||||
| 7,71 | 0,771 |
5. Измеряем углы отклонения маятника после выстрела в него пулями различной массы с учетом случайной и систематической (приборной) погрешностей измерений a по формуле (5):
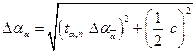 . (5)
. (5)
6. Проводим расчет скорости полета пули по формуле (6) и о погрешность измерений скорости по формуле (7):
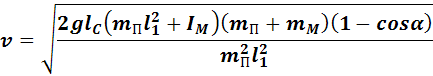
, (6)
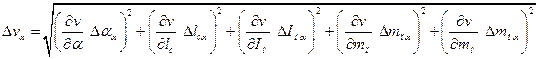 . (7)
. (7)
7. Результаты измерений, расчетов, оценок погрешностей измерений сводим в таблицу 2.
 Таблица 2
Таблица 2
| lc=(0,120 ± 0,005)м; l1=(0,23 ± 0,005)м; Iм= (1,67 ± 0,08)·10-3 кг·м2; mм=(0,088 ± 0,002) кг. | ||||||||||||||
| mп1=(0,0052 ± 0,0005) кг (дюраль с отверстием) | mп2=(0,0068 ± 0,0005) кг (дюраль) | mп3=(0,0140 ± 0,0005) кг (сталь с отверстием) | ||||||||||||
| α1 | α2 | α3 | α4 | α5 | α1 | α2 | α3 | α4 | α5 | α1 | α2 | α3 | α4 | α5 |
| 10, | ||||||||||||||
| α1ср= 9,460 Δa1α=1,260 | α2ср= 13,50 Δa2α=1,450 | α3ср= 24,10 Δa3α=1,570 | ||||||||||||
| v1ср, м/c | v2ср, м/c | v3ср, м/c | ||||||||||||
| 2,01 | 2,26 | 2,20 | ||||||||||||
| Δv1α, м/c | Δv2α, м/c | Δv3α, м/c | ||||||||||||
| 0,15 | 0,2 | 0,12 |
8. Определяем потери механической энергии по формуле (8):
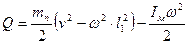 . (8)
. (8)
Таблица 3
| mм=(0,088 ± 0,002) кг; lc=(0,120 ± 0,005) м l1=(0,23 ± 0,005)м; Tср ± ΔTα = (0,79 ± 0,0005) c. | ||||
| mпi ± Δmпi | 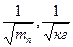
| 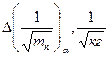 
| αсрi ± Δααi | Qср., Дж |
| 0,0052 ± 0,0005 | 13,87 | 0,7 | 9,460 ± 1,260 | -0,56·10-3 |
| 0,0068 ± 0,0005 | 12,13 | 0,4 | 13,50 ± 1,450 | -0,01 |
| 0,0140 ± 0,0005 | 8,45 | 0,15 | 24,10 ± 1,570 | -0,01 |
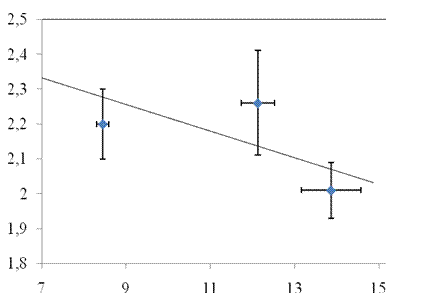
9. Строим график зависимости в координатах «v - 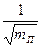 » с учетом погрешности измерений скорости и массы пуль.
» с учетом погрешности измерений скорости и массы пуль.
Заключение: по данным лабораторного эксперимента построена графическая зависимость в координатах «v - 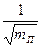 »,являющаяся линейной, что соответствует аналитической зависимости для скорости полета пули от ее массы до неупругого соударения с физическим маятником.
»,являющаяся линейной, что соответствует аналитической зависимости для скорости полета пули от ее массы до неупругого соударения с физическим маятником.


Вывод:
1. На основе законов сохранения момента импульса и механической энергии получена аналитическая зависимость для скорости полета пули и потери механической энергии в момент ее неупругого взаимодействия в системе «пуля – стержень».
2. Определены численные значения скорости полета пули.
3. Графически установлена линейная зависимость между скоростью пули и величиной, обратной корню квадратному из массы пули.
4. Определены численные значения потери механической энергии для трех случаев взаимодействия пуль, изготовленных из различных материалов.
Общие правила построения графиков
1. Графики строятся в программах Microsoft Word, Origion. Pro (или на миллиметровой бумаге карандашом ½ тетрадного листа).
2. Используется прямоугольная система координат с РАВНОМЕРНОЙ разметкой осей. Значения аргумента откладываются по оси X, значения функции – по оси Y.
3. Масштаб и начало координат выбираются так, чтобы экспериментальные точки располагались по всей площади рисунка.
4. Единица масштаба должна быть кратна 1×10 n, 2×10 n 3×10 n и т. д., где n = …-2, -1, 0, 1, 2, ….
5. Рядом с осью дается буквенное обозначение, порядок и размерность физической величины.
6. Под графиком – полное название графика СЛОВАМИ.
7. Никаких линий и отметок, поясняющих построение точек на графикe, наносить нельзя.
Примеры:
| ВЕРНО | НЕВЕРНО |

|