σmax=N/Aнетто≤[σ](1)
σmax=N/Aбрутто≤[σ](2)
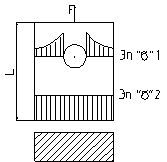
По каким сечениям выполняются проверка прочности растянутого бруса по касательным и нормальным напряжениям.
При раст/сжат касательные напряжения не учитываем.
τα=σ/2*sin2α Если sin2α=1 (α =450), то τ=1/2 σ. τmax= σ/2≤[τ]
Для определения какой деф используют коэф Пуассона?
μ = γ = ε1/ε=Δb/Δl*L/b; ε1= Δb/b-относительное сужение; ε = Δl/l-относительное удлинение; Коэф используется для любой деф. 0≤μ≤0,5.
Приведите Закон Гука при раст/сжат.
Y=c*X; F=c* Δl; Δl=Fl/EA; σ=E ε;
Как определить продольные деф и перемещения поперечных сечений бруса?
ΔL=Lнач – Lкон; ΔL= Fl/EA;
Изложите расчёт прочности при растяжении/сжатии. Типы решаемых задач.
σmax=F /A≤[σ].
Типы реш. задач:
1. Проверка прочности. σmax ≤[σ]- конструкция годится для испытаний.
2. Подбор сечения бруса. A=F/[σ];
3. Грузоподъёмность F≤A[σ]
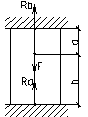12.Статически неопределимые задачи при растяжении. Свойства статически неопределимых систем.
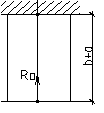
∑Z=0
Ra-?
Rb-? ΔlRa= ΔlF; ΔlRa=Ra*(a+b)/EA; ΔlF=Fa/EA; Ra=Fa/(a+b);
Св-во: всегда имеются «лишние» связи.
Какие площадки и напряжения наз главными?
Площадка в точке наз главной, если касательное напряжение в ней равно нулю(τ=0).
Дать определение одноосного плоского и объёмного напряженного состояний.
σ1> σ2> σ3
Везде τ=0
Показаны главные площадки.
15.Закон парности касательных напряжений для плоского напряжённого состояния. σ1<σ2 Круг Мора.
Как расположены площадки с наибольшими касательными напряжениями по отношению к главным?
Приведите закон Гука для объёмного напряжённого состояния.
ε1=1/E[σ1-μ(σ2+σ3)]
ε2=1/E[σ2-μ(σ1+σ3)]
ε3=1/E[σ3-μ(σ1+σ2)]
Определение осевых полярных и центральных моментов.
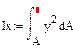
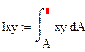
-центробежный момент инерции.
Какие оси наз главными осями инерции?
Главными осями инерции наз оси, относительно которых Ixy=0, а Ix и Iy – экстремальны.
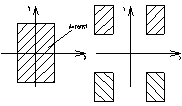
Как увеличить значение осевого момента инерции сечения при постоянной площади А?
Необходимо разрезать площадку и раздвинуть части. Чем больше раздвинуть, тем больше момент инерции.
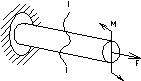
Какой вид деф наз кручением?
Если моменты действуют относительно продольной оси стержня.
Как определить крутящий момент стержня?
m1= ∑Mот.ч.=М
Какие напряжения возникают в поперечном сечении круглого стержня при кручении и как они распределены?
При кручении возникает деф закручивания. τ=Mz/Ip*ρ 0≤ρ≤r
τmax=Mz*r/Ip=Mz/Wp≤[τ];
[τ]=[σ]/2;
25. imax=Mz/Wp≤[τ]; [τ]=[σ]/2;
При кручении возникает деф закручивания стержня относительно оси Z. Деформация определяется углом закручивания. φ=Mzlнач/IpG (рад), где Mz-крутящий момент, lнач-начальная длина стержня, Ip-полярный момент,G-модуль упругости 2-го рода.
Условие жёсткости: φmax=Mzlнач/IpG≤[φ]
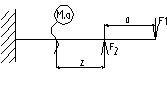
Как определяются поперечная сила и изгибающий момент в поперечном сечении балок.
Q=∑yот.ч.; M=∑Mот.ч.; Q=F1-F2; Mz=-F1(a+z)+F2*z;
Какой вид деф наз прямым плоским изгибом. Чистый и поперечный изгиб.
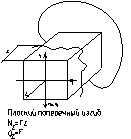
Правила знаков для Q и M.
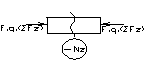
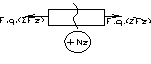
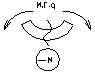
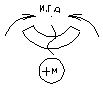
Приведите диф зависимости между q, Q, M.
q = dQ/dz→tgα; Q = dM/dz→tgβ;
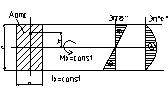
30.Покажите распределение нормальных и касательных напряжений по высоте поперечного сечения балки.
σ=±Mx/Ix*y; 0≤y≤h/2
τ=QSxотс/Ix*b; Sxотс=Aотс*y;
Какие точки поперечного сечения балки являются наиболее опасными по касательным и нормальным напряжениям?
Наиболее удалённые – по нормальным напряжениям;
Точки, лежащие по нейтральному слою- по касательным напряжениям.