Анализ инженерно-геологических условий строительной площадки

Решение задач

Механики грунтов

 

 

Учебное пособие

 

Федеральное агентство по образованию

 

Государственное образовательное учреждение высшего профессионального образования

Вятский государственный университет

 

Факультет строительства и архитектуры

Кафедра строительного производства

 

 

А.В. Никулин

М.В. Крутикова

 

 

Решение задач

Механики грунтов

 

	Рекомендовано Ученым советом Вятского государственного университета в качестве учебного пособия

 

 

Киров 2008

 

Печатается по решению редакционно-издательского совета

Вятского государственного университета

 

УДК 624.121(07)

Н651

 

Рецензенты: Главный инженер проекта ООО «Институт
«Кировгражданпроект» А.А. Климович, начальник
строительного отдела Т.В. Попова;

кафедра строительных конструкций, доцент кафедры СК, М.А. Жандаров

 

 

Никулин, А.В. Решение задач механики грунтов: учебное пособие/
А.В. Никулин, М.В. Крутикова. – Киров: Изд-во ВятГУ, 2007. – 49 с.

 

В учебном пособии рассматриваются методы решения основных задач механики грунтов. Предназначено для студентов заочной формы обучения факультета строительства и архитектуры ВятГУ, также может быть полезно молодым инженерам-проектировщикам и лицам, интересующимся вопросами расчета и проектирования оснований и фундаментов.

 

Редактор Н.Ю. Целищева

 

			Усл. печ. л. Печать Aficio 1022 Бесплатно

 

 

Текст напечатан с оригинала-макета, предоставленного авторами.

610000, г. Киров, ул. Московская, 36

Оформление обложки, изготовление – ПРИП ВятГУ.

© А.В. Никулин, М.В. Крутикова, 2008.

© Вятский государственный университет, 2008.

ОГЛАВЛЕНИЕ

 

введение. 4

1. Анализ инженерно-геологических условий строительной площадки. 5

2. Определение напряжений в грунтовом массиве от действия
местной нагрузки на его поверхности. 16

3. Определение напряжений в массиве грунта от действия собственного веса (бытовое давление) 20

4. Определение осадки фундамента (штампа) 24

5. Определение устойчивости подпорной стенки. 33

ЗАКЛЮЧЕНИЕ. 41

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 42

Приложение А (справочное)
КЛАССИФИКАЦИЯ СКАЛЬНЫХ ГРУНТОВ.. 43

Приложение Б (справочное)
УПРОЩЕННАЯ КЛАССИФИКАЦИЯ ГРУНТОВ.. 44

Приложение В (справочное)
КЛАССИФИКАЦИЯ ГРУНТОВ ПО КОНСИСТЕНЦИИ.. 45

Приложение Г (справочное)
КЛАССИФИКАЦИЯ ГРУНТОВ ПО СЖИМАЕМОСТИ.. 46

Приложение Д (справочное)
ТАБЛИЧНЫЕ НАЗНАЧЕНИЯ КОЭФФИЦИЕНТА ПРОСАДОЧНОСТИ.. 47

Приложение Е (справочное)
КЛАССИФИКАЦИЯ ГРУНТОВ ПО ГРАНУЛОМЕТРИЧЕСКОМУ
СОСТАВУ.. 48

Приложение И (справочное)
ОПРЕДЕЛЕНИЕ СЛОЖНОСТИ ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ УСЛОВИЙ ПЛОЩАДКИ СТРОИТЕЛЬСТВА.. 49

Приложение К (справочное)
ПЛОТНОСТЬ СЛОЖЕНИЯ ПЕСЧАНЫХ ГРУНТОВ.. 50

Приложение Л (справочное)
ЗНАЧЕНИЕ КОЭФФИЦИЕНТОВ α. 51

Приложение М (справочное)
ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ ЭКВИВАЛЕНТНОГО СЛОЯ Аω.. 52

 

Введение

 

Механика грунтов изучает напряженно-деформированное состояние грунтов и грунтовых массивов, условия прочности грунтов, давление на ограждения, устойчивость грунтовых массивов против сползания и разрушения, взаимодействие грунтовых массивов с сооружениями и ряд других вопросов. Целью механики грунтов является оценка состояния грунтов в настоящий момент и прогноз дальнейшего поведения грунтов, прогноз происходящих в них процессов.

Знание механики грунтов позволяет грамотно оценивать несущую способность грунтов основания, совершенствовать проектные и технологические решения в области фундаментостроения, что приводит к существенной экономии материальных и трудовых ресурсов, сокращению сроков строительства зданий и сооружений. Недооценка несущей способности грунтов оснований приводит к удорожанию строительства. С другой стороны, переоценка строительных свойств грунтов часто бывает причиной аварий сооружений.

Механика грунтов тесно связана с инженерной геологией, сопротивлением материалов, теориями упругости, пластичности и ползучести, строительной механикой, методами математического анализа.

Основной целью настоящих методических рекомендаций является обучение студента теоретическим основам и практическим навыкам решения основных задач механики грунтов. Очередность изложения разделов в методических рекомендациях совпадает с очередностью задач в контрольной работе. Каждая глава посвящена решению одной из задач контрольной работы и включает в себя теоретические предпосылки и практический пример решения.

Контрольная работа оформляется в виде расчетно-пояснительной записки, выполненной на листах формата А4. В состав записки включаются:

· титульный лист с обязательным указанием учебного заведения, фамилии, имени и отчества исполнителя, его шифра, номера группы, а также номера задания на контрольную работу;

· копия задания на контрольную работу;

· расчеты, представленные отдельно по каждой задаче и включающие в себя исходные данные, подробные промежуточные вычисления, расчетные схемы со всеми необходимыми обозначениями и размерами, результаты и выводы по итогам решения задачи;

· библиографический список.

Все расчетные данные и показатели должны сопровождаться «техническими» единицами измерения (кг, т, кг/м², т/м³ и т.д.), а расчеты – ссылками на нормативные документы и используемую литературу.

При решении задач контрольной работы растительный слой и насыпной грунт не учитывается.

 

 

Анализ инженерно-геологических условий строительной площадки

 

Анализ инженерно-геологических условий строительной площадки включает в себя следующие этапы:

· определение физико-механических характеристик грунтов;

· построение инженерно-геологического разреза строительной площадки;

· подготовка заключения по строительной площадке.

В соответствии с п. 1.4[1], проектирование основания без соответствующего
инженерно-геологического обоснования или при его недостаточности не допускается.

Определение физико-механических характеристик грунтов производится отдельно для каждого слоя грунта по известным формулам механики грунтов [38]. Исходными данными служат данные геологических изысканий (литологическое описание и размеры слоев грунта в пределах скважины или шурфа, а также расчетные характеристики грунтов каждого слоя, определяемые лабораторными или полевыми испытаниями).

Результатом определения физико-механических характеристик грунтов служит характеристика каждого слоя грунта по [2] (см. прил. АЕ и И), а также заключение о возможности или невозможности использования данного слоя грунта в качестве естественного основания.

Не могут служить естественным основанием:

· сильносжимаемые грунты;

· песчаные грунты рыхлые;

· пылевато-глинистые грунты просадочные или текучей консистенции.

В случае, если по грунту первого слоя данные не представлены, то для этого грунта физико-механические характеристики не определяют. В случае, если по грунту последнего четвертого слоя из всех данных представлено только значение предела прочности грунта на одноосное сжатие R _c, то такой грунт считается скальным (полускальным при значении R _c < 50 кг/см²) и для него следует определить наименование по прил. А.

Пример 1. Определить физико-механические характеристики грунтов и дать характеристику грунта каждого слоя. Исходные данные представлены в табл. 1.

Слой № 1:

Удельный вес сухого грунта (скелета грунта) определяем по формуле

т/м³.

Пористость грунта определяем по формуле

.

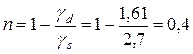Таблица 1

Физико-механические характеристики грунтов

Гранулометрический состав, %, мм	Заданные расчетные характеристики	Вычисляемые расчетные характеристики
№ слоя	крупнее 10	10-2	2-1	1-0,5	0,5-0,25	0,25-0,1	0,1-0,05	0,05-0,01	0,01-0,005	менее 0,005	γS, т/м3	γ, т/м3	ω	ωР	ωL	φ, град	с, кг/см2	Е, кг/см2	k, см/с	γd, т/м3	n	e	IР	IL	mv, см2/кг	Sr	eL	Iss
											2,7	1,93	0,2	0,18	0,3		0,23		2·10-6	1,61	0,4	0,68	0,12	0,17	0,0044	0,79	0,81	0,08
											2,7	2,03	0,2	0,15	0,21		0,12		2,7·10-6	1,69	0,37	0,6	0,06	0,83	0,0062	0,9	0,57	-0,019
											2,65		0,25				0,01		3·10-2	1,6	0,4	0,66			0,0032
											2,76		0,27	0,24	0,44		0,47		6·10-8	1,57	0,43	0,76	0,2	0,15	0,002	0,98	1,21	0,26

Коэффициент пористости грунта определяют по формуле

.

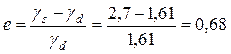Число пластичности грунта определяют по формуле

.

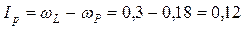По числу пластичности, как и по содержанию глинистых частиц, грунт является суглинком. Упрощенная классификация грунтов приведена в прил. Б.

Число текучести грунта определяют по формуле

.

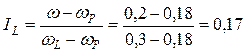По числу текучести суглинок имеет полутвердую консистенцию. Классификация пылевато-глинистых грунтов по консистенции приведена в прил. В.

 

Коэффициент относительной сжимаемости грунта определяли поформуле

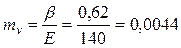см²/кг.

По коэффициенту относительной сжимаемости грунт следует отнести к малосжимаемому. Классификация грунтов по коэффициенту относительной сжимаемости приведена в прил. Г. Коэффициент β принимают для пылеватых и мелких песков – 0,8; супесей – 0,74; суглинков – 0,62; глин – 0,4.

Степень влажности грунта определяют по формуле

.

Коэффициент пористости грунта на границе текучести определяют по формуле

.

Коэффициент просадочности грунта определяют по формуле

.

Рассчитанный коэффициент просадочности меньше табличного значения равного 0,17 (прил. Д), следовательно, грунт обладает просадочными свойствами.

Таким образом, грунт первого слоя представляет собой суглинок полутвердый, просадочный, малосжимаемый, и который естественным основанием служить не может.

 

Слой № 2:

γ_d = 1,69 т/м³; n = 0,37; e = 0,6; I_p = 0,06. По числу пластичности, как и по содержанию глинистых частиц, грунт является супесью.

I_L = 0,83. По числу текучести супесь имеет пластичную консистенцию.

m_v = 0,0062 см²/кг. По коэффициенту относительной сжимаемости грунт следует отнести к малосжимаемому.

S_r = 0,9; e_L = 0,57. Степень влажности у рассматриваемого грунта более 0,8, поэтому следует считать, что данный грунт просадочными свойствами не обладает.

Таким образом, грунт второго слоя представляет собой супесь пластичную, малосжимаемую, непросадочную, и которая может служить естественным основанием.

Слой № 3:

γ_d = 1,6 т/м³; n = 0,4.

Для данного грунта значения ω_L и ω_Р не приведены (равны 0), следовательно, I_Р также будет равно 0. По числу пластичности, как и по содержанию глинистых частиц, грунт относится к песчаным. Упрощенная классификация грунтов приведена в прил. Б.

В данном грунте содержится 56 % по массе частиц с диаметром более 0,25 мм, следовательно, по гранулометрическому составу грунт относится к пескам средней крупности. Классификация песчаных грунтов по гранулометрическому составу приведена в прил. Е.

e = 0,66. По коэффициенту пористости песок средней крупности следует отнести к средней плотности. Классификация песчаных грунтов по плотности сложения приведена в прил. И.

m_v = 0,0032 см²/кг. По коэффициенту относительной сжимаемости грунт следует отнести к малосжимаемому.

S_r = 1. По степени влажности грунт следует отнести к насыщенному водой. По водонасыщенности (степени влажности) S_r песчаные грунты разделяют на маловлажные при 0 < S_r ≤ 0,5, влажные при 0,5 < S_r ≤ 0,8, насыщенные водой при 0,8 < S_r ≤ 1.

Коэффициент неоднородности песка определяли по соотношению

,

где d₆₀ – диаметр частиц, меньше которого в данном грунте содержится 60 % (по массе), d₁₀ – диаметр частиц, меньше которого в данном грунте содержится 10 % (по массе).

При C_И ≤ 3 – песок однородный, при C_И > 3 – песок неоднородный.

Значения d₆₀ и d₁₀ определяли графически, путем построения полулогарифмического графика гранулометрического состава (в масштабе). В соответствии с рассчитанными в табл. 2 данными, по оси абсцисс откладывали натуральные логарифмы диаметров частиц, по оси ординат – процентное содержание частиц, меньше размера фракций.

Таблица 2

Результаты расчета

Наименование определений	Размер фракций, мм
крупнее 10	10-2	2-1	1-0,5	0,5-0,25	0,25-0,1	0,1-0,05	0,05-0,01	0,01-0,005	менее 0,005
Процент от общего количества
Сумма процентов менее данного диаметра
Натуральный логарифм данного диаметра	-	2,3	0,63		-0,7	-1,4	-2,3	-3,0	-4,6	-5,3

 

После построения графика из точек на оси ординат, соответствующих
10 % и 60 %, опускаем на график перпендикуляры, а затем из полученных точек пересечения опускаем вторые перпендикуляры на ось абсцисс, получая значения натуральных логарифмов lnd₁₀ = -4,38 и lnd₆₀ = -1,09 соответственно (рис. 1). Возводя экспоненту в степень по полученным значениям, определяют d₆₀ и d_10.

.

.

.

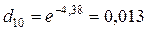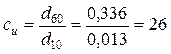По коэффициенту неоднородности песок следует отнести к неоднородному.

 

 

Рис. 1. Полулогарифмический график гранулометрического состава

 

Таким образом, грунт третьего слоя представляет собой песок средней крупности, средней плотности, насыщенный водой, неоднородный, который может служить естественным основанием.

 

Слой № 4:

γ_d = 1,57 т/м³; n = 0,43; e = 0,76; I_p = 0,2. По числу пластичности, как и по содержанию глинистых частиц, грунт является глиной.

I_L = 0,15. По числу текучести глина имеет полутвердую консистенцию.

m_v = 0,002 см²/кг. По коэффициенту относительной сжимаемости грунт следует отнести к малосжимаемому.

S_r = 0,98; e_L = 1,21; I_ss = 0,26. Рассчитанный коэффициент просадочности больше табличного значения, равного 0,24, следовательно, грунт просадочными свойствами не обладает.

Таким образом, грунт четвертого слоя представляет собой глину полутвердую, малосжимаемую, непросадочную и может служить естественным основанием.

 

Инженерно-геологические разрезы площадки строят в целях определения напластования, показателей состава и положения уровней подземных вод.

При этом руководствуются данными инженерно-геологических изысканий (технические отчеты, планы тахеометрических съемок, литологические описания грунтов, геологические колонки и др.).

Разрез строят развернутым по вертикальной плоскости, расстояния между буровыми скважинами берутся из плана стройплощадки, а мощность пластов – с геологических колонок, приведенных в задании. На разрезе обозначается уровень подземных вод и отмечаются места забора образцов, границы смены слоев грунта соединяют между буровыми скважинами прямыми линиями, над которыми отмечают уклоны слоев грунта.

Построение разреза строительной площадки рекомендуется проводить на миллиметровой бумаге в масштабе 1:100–1:500. Условные обозначения принимаются в соответствии с ГОСТ 21.302-96.

 

Пример 2. Построить геологический разрез между буровыми скважинами № 1 и 2, расположенными на расстоянии 20 м друг от друга. Исходные данные приведены в табл. 3.

 

Таблица 3

Описание буровых скважин

№ скважины и абсолютная отметка устья	№ слоя	Геологический возраст	Описание горных пород	Глубина залегания подошвы слоя, м	Глубина залегания уровня воды, м
1 102,6		аQ3	Суглинок желто-бурый легкий	1,2	4,0
	аQ3	Супесь серая легкая	6,2
	аQ3	Песок средней крупности серый	13,9
	аQ3	Глина коричневая пылеватая	15,0
2 100,9		аQ3	Суглинок желто-бурый легкий	1,5	2,3
	аQ3	Супесь серая легкая	8,0
	аQ3	Песок средней крупности серый	14,3
	аQ3	Глина коричневая пылеватая	15,0

 

Из описания видно, что скважиной вскрыты (сверху вниз) верхнечетвертичные отложения, представленные четырьмя слоями: суглинком желто-бурым легким, супесью серой легкой, песком средней крупности серым и глиной коричневой пылеватой.

Пример построения геологического разреза представлен на рис. 2. В нижней части листа оставляют три строки для характеристики скважин и указания расстояний между ними. Намечают начало и откладываем вправо длину разреза в принятом масштабе. Слева строят шкалу абсолютных отметок (геодезическую рейку) с таким расчетом, чтобы максимальная отметка была несколько выше верхней точки рельефа, а минимальная  ниже забоя самой глубокой скважины. К шкале «привязывают» скважины.

 

 

Рис. 2. Пример построения геологического разреза

Вдоль линии скважины размечают границы слоев и проставляют их абсолютные отметки, которые вычисляют как разность абсолютной отметки устья скважины и глубин залегания соответствующих слоев. Например, в скважине 2 абсолютная отметка границы между вторым и третьим слоями равна: 100,9  8,0 = 92,9 м.

В интервале каждого слоя условными обозначениями отмечают состав и относительный возраст пород.

После этого справа от линии скважины обозначают абсолютные отметки уровней подземных вод и проводят уровень подземных вод пунктирной линией. Построение разреза заканчивают обозначением уклонов слоев грунта.

 

Заключение по строительной площадке должно включать указание места расположения площадки, характеристику рельефа и сложности инженерно-геологических условий, описание грунтов по слоям с заключением о возможности использования слоев в качестве естественного основания.

Определение сложности инженерно-геологических условий площадки строительства проводится в соответствии с прил. И.

Пример 3. Подготовить заключение по строительной площадке на основании исходных данных, изложенных в примерах 1 и 2.

Строительная площадка расположена в г. Екатеринбурге, относится ко второй категории сложности. Характер рельефа спокойный, с уклоном
i = 0,085 и абсолютными отметками 100,9 – 102,6. На площадке пробурено две скважины. При бурении были вскрыты следующие грунты:

1) Суглинок желто-бурый легкий, мощностью от 1,2 до 1,5 м, полутвердый, просадочный, малосжимаемый, естественным основанием служить не может.

2) Супесь легкая серая, мощностью от 5,0 до 6,5 м, пластичная, малосжимаемая, непросадочная, может служить естественным основанием. Уровень подземных вод обнаружен на глубине от 2,3 до 4,0 м от дневной поверхности, воды не агрессивны по отношению к бетону и раствору.

3) Песок средней крупности серый, мощностью от 6,3 до 7,7 м, средней плотности, насыщенный водой, неоднородный, может служить естественным основанием.

4) Глина коричневая пылеватая, слой до конца не пройден, полутвердая, малосжимаемая, непросадочная, может служить естественным основанием. Является водоупором.

Залегание пластов выдержанное (согласованное), с уклоном от 0,1 до 0,175, выклинивание пластов не наблюдается.

2. Определение напряжений в грунтовом массиве от действия
местной нагрузки на его поверхности

 

Действие равномерно распределенной нагрузки [38] в условиях пространственной задачи возникает тогда, когда к поверхности линейно деформируемого полупространства приложена местная нагрузка, распределенная по площади квадрата, прямоугольника, круга, эллипса и др. Значения вертикальных сжимающих напряжений σ_z в любой точке полупространства от действия нагрузки интенсивностью р, равномерно распределенной по площади прямоугольника размером l x b, были впервые получены А. Лявом. Практический интерес представляют значения сжимающих напряжений, проведенных из центра σ_zО и из углов σ_zС загруженной площади (рис. 3).

,

где α – определяется по прил. К, в зависимости от величин n = l/b и
m = 2 · z / b (l – длинная сторона, b – короткая сторона прямоугольника загружения, z – расстояние от точки до поверхности приложения нагрузки).

,

где α – определяется по прил. Л, в зависимости от величин n = l/b и
m = z / b.

Рис. 3. Расчетная схема для определения сжимающих напряжений

под центром и под углом прямоугольника с равномерно распределенной нагрузкой

 

Для определения сжимающих напряжений в любой точке полупространства М применяют метод угловых точек, используя формулу

.

На рис. 4 представлены различные варианты расположения точки М. В методе угловых точек всегда принимают l ≥ b.

На рис. 4 а и б точка М расположена в пределах площади загружения. Для этих случаев площадь загрузки разбивают, соответственно, на два и четыре прямоугольника так, чтобы точка М была угловой точкой для каждого из них. Тогда напряжение σ_zМ находят суммированием напряжений под угловыми точками площадей загружения. Соответственно для первого и второго случаев

и .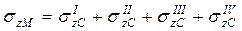

Рис. 4. Схема для расчета напряжений методом угловых точек

 

На рис. 4 в точка М расположена вне пределов площади загружения. Для данного случая точку М можно представить как угловую точку фиктивных площадей загружения I и II, при этом в пределах площадей III и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжение σ_zМ определяется по выражению

.

 

Пример 4. Определить напряжение в точке М от распределенной нагрузки, интенсивностью р = 2 кг/см², при b = 1,5 м, l = 3 м, z = 3 м, а₁ = а₂ = 1,5 м. Расчетная схема представлена на рис. 5 а.

 

По методу угловых точек загруженную площадь делим на два прямоугольника таким образом, чтобы точка М попадала в угол каждого из них (рис. 5 а).

Рис. 5. Расчетные схемы

 

 

Далее определяем коэффициенты α для каждого из прямоугольников как функцию значений n и m (прил. Л), учитывая, что прямоугольник 1 и прямоугольник 2 равны (рис. 5 а).

.

Напряжение в точке М определяем как сумму напряжений от прямоугольников 1 и 2, учитывая, что эти прямоугольники равны (рис. 5 а).

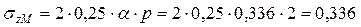кг/см².

 

Пример 5. Определить напряжение в точке М от распределенной нагрузки, интенсивностью р = 2 кг/см², при b = 3 м, l = 3 м, z = 3 м, а₁ = а₂ = 1,5 м. Расчетная схема представлена на рис. 5 б.

 

Точка М находится под центром большого (загруженного) и малого (незагруженного) прямоугольников (рис. 5 б).

Далее определяем коэффициенты α для большого и малого прямоугольников как функцию значений n и m (прил. Л).

,

.

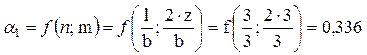Напряжение в точке М, определяем как разность напряжений большого прямоугольника (с фиктивной загрузкой от малого прямоугольника) и малого прямоугольника (фиктивной загрузки) (рис. 5 б):

кг/см².

 

 

3. Определение напряжений в массиве грунта
от действия собственного веса (бытовое давление)

 

На практике используют упрощенную методику расчета, основанную на предположении о том, что природные напряжения в массиве грунта формируются только под действием собственного веса [3  8]. Также принято считать, что все деформации массива от собственного веса прекратились и напряжения полностью стабилизировались.Практический интерес представляют значения сжимающих напряжений σ_z.

При горизонтальной поверхности массива грунта однородного напластования сжимающие напряжения на глубине z определяются выражением

,

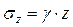где γ – удельный вес грунта.

Эпюра природных напряжений массива грунта однородного напластования при горизонтальной поверхности будет иметь вид треугольника (рис. 6 а).

При неоднородном напластовании или наличии подземных вод, а также при горизонтальной поверхности напряжения от собственного веса грунтов будут определяться отдельно для каждого слоя (рис. 6 б). Причем удельный вес грунта, расположенного ниже уровня подземных вод, будет определяться с учетом взвешивающего действия воды γ_sb:

,

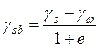где γ_s – удельный вес частиц грунта; γ_ω – удельный вес воды, принимается равным 1 т/м³; е – коэффициент пористости грунта.

 

Рис. 6. Эпюры распределения напряжений от собственного веса грунтов

Если ниже уровня подземных вод залегает водоупорный слой, то на его кровле дополнительно учитывают давление от столба вышерасположенной воды равное γ_ω · h_ω (рис. 6 в).

 

Пример 6. Определить напряжения от собственного веса грунтов и построить эпюру распределения данных напряжений по скважине № 1. Исходные данные см. примеры 1 и 2.

 

Первоначально на основании данных инженерно-геологических изысканий (см. пример 2) строим в масштабе геологическую колонку с указанием мощности слоев грунта, уровней подземных вод и водоупора (рис. 7). Далее на основании результатов определения физико-механических характеристик грунтов (см. пример 1) для каждого слоя грунта указываем необходимые для дальнейшего расчета данные.

 

 

Рис. 7. Совмещенная схема геологической колонки и эпюры

распределения напряжений от собственного веса грунтов

 

 

Расчет напряжений от собственного веса грунтов проводим последовательно, начиная от поверхности земли. Расчетные точки располагаем на поверхности земли, на границах слоев грунтов, на уровнях подземных вод и водоупора.

На поверхности земли дополнительная пригрузка отсутствует, поэтому напряжение равно .

Напряжение на границе между первым и вторым слоями грунта определяем как сумму напряжений σ₁ и от собственного веса грунта первого слоя:

т/м³.

Напряжение на уровне подземных вод определяем как сумму напряжений σ₂ и от собственного веса грунта второго слоя на расстоянии от его кровли до уровня подземных вод:

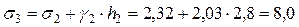т/м³.

Напряжение на границе между вторым и третьим слоями грунта определяем как сумму напряжений σ₃ и от собственного веса грунта второго слоя на расстоянии от уровня подземных вод до его подошвы, при этом учитываем взвешивающее действие воды на частицы грунта второго слоя

т/м³,

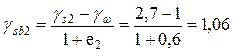где т/м³.

Напряжение на границе между третьим и четвертым слоями грунта определяем как сумму напряжений σ₄ и от собственного веса грунта третьего слоя, при этом учитываем взвешивающее действие воды на частицы грунта третьего слоя

т/м³,

где т/м³.

На кровле четвертого слоя напряжение определяем с учетом дополнительного напряжения от столба вышерасположенной воды как сумму напряжений σ₅ и от собственного веса столба вышерасположенной воды:

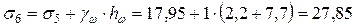т/м³.

На уровне нижней границы скважины напряжение определяем как сумму напряжений σ₆ и от собственного веса грунта четвертого слоя на расстоянии от его кровли до уровня забоя скважины:

т/м³.

Далее по полученным значениям σ₁–σ₇ в масштабе строим эпюру распределения напряжений от собственного веса грунтов, которую совмещаем с уже построенной геологической колонкой (рис. 7).