Преподаватель Гринченко К.Н.
Конспект практического занятия по информатике.
Тема урока: «Компьютерная модель «Лисы и кролики»
Цели урока:
· Образовательные
1. Сформировать умение создавать и исследовать биологические модели.
2. закретить умение построения моделей в электронных таблицах OpenOffice.org Calc.
· Развивающие:
§ формирование умения самостоятельно работать;
§ Развивать логику, умение анализировать, сравнивать, делать выводы, высказывать свою мысль;
§ формирование навыков ИКТ-компетентности;
· Воспитательные:
§ Повышение познавательного интереса к предмету;
§ Воспитание бережного отношения к окружающей среде.
Хол урока:
Организационный этап. Мотивационный модуль.
Основная часть. Объяснительный модуль.
Изучение нового материала.
(Слайд № 1)
Сегодня мы продолжим изучение биологических моделей и познакомимся с моделью «хищник-жертва». Запишите число и тему урока «Исследование биологических моделей. Модель Лотки-Вольтерра».
В своих ежедневных рассуждениях и наблюдениях мы, сами того не зная, руководствуемся законами и идеями, открытыми много десятилетий назад. Рассматривая проблему хищник – жертва, мы догадываемся, что жертва тоже влияет на хищника. Чем бы обедал лев, если бы не было антилоп; что бы делали управленцы, если бы не было рабочих.
(Слайд № 2)
В 1925 году известный итальянский математик Вито Вольтерра, беседуя за обедом со своим будущим зятем, ихтиологом по специальности, заинтересовался популяционной динамикой рыб. Например, он узнал, что снижение вылова рыбы во время первой мировой войны привело к увеличению доли хищной рыбы в уловах. Результатом осмысления таких фактов стали предложенные им модели для описания внутривидового взаимодействия. Одновременно с Вольтерра данной проблемой занимался и другой учёный – Лотка. Поэтому данная модель была названа моделью Лотки-Вольтерра. При составлении модели были предложены следующие условия (гипотезы): (Слайд № 3)
|
|
1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано.
2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.
3. Хищные виды поедают жертвы, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов.
4. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида за единицу времени пропорционален численности вида.
Перечисленные гипотезы позволяют описывать сложные живые системы при помощи систем обыкновенных дифференциальных уравнений.
Данные системы имеют большое количество применений, например, для моделирования систем «хищник-жертва», «паразит-хозяин», конкуренции и других видов взаимодействия. Но, есть одно ограничение модели – ее замкнутость. Рассматриваемая система взаимодействия не должна получать дополнительных ресурсов со стороны, и участники системы взаимодействуют с одинаковой эффективностью на рассматриваемом промежутке времени.
Теперь опишем модель. (Слайд № 4) Пусть имеется некоторый остров в океане. На данном острове обитают лисы (foxes) и кролики (rabbits). Лисы питаются кроликами, кролики питаются травой (grass). Трава имеется в неограниченном количестве и вычисляется в процентах от площади острова. Нужно выяснить: возможно ли совместное существование этих двух видов? И как будет вести себя модель при крайних состояниях, т. е. когда либо в системе отсутствуют лисы или отсутствуют кролики?
|
|
Теперь необходимо составить формальную модель.
От чего будет зависеть численность популяции кроликов на следующий год? (Ответ: от количества кроликов за этот год, количества лис, прирост популяции и естественная смертность в популяции) (Слайд № 5-6)
Верно, поэтому можно записать следующее уравнение:
Rn+1 = (Krb*Rn*G – Krd*Rn*Fn)*t + Rn, где
Rn+1 – численность популяции кроликов на следующий период времени измерения;
Rn – численность популяции кроликов на данный период времени;
Krb – коэффициент рождаемости кроликов;
Krd – коэффициент смертности кроликов;
G – количество травы;
Fn – численность популяции лис на данный период времени;
t – период времени между измерениями популяций.
А от чего будет зависеть популяция лис? (Ответ: от количества кроликов и самих лис).
(Слайд № 7) Таким образом численность популяции лис запишется следующим уравнением:
Fn+1 = (Kfb*Rn*Fn – Kfd*Fn)*t + Fn, где
Fn+1 – численность популяции лис на следующий период времени измерения;
Fn – численность популяции лис на данный период времени;
Kfb – коэффициент рождаемости лис;
Kfd – коэффициент смертности лис.
Система уравнений (Слайд № 8)
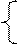Rn+1 = (Krb*Rn*G – Krd*Rn*Fn)*t + Rn
Fn+1 = (Kfb*Rn*Fn – Kfd*Fn)*t + Fn,
получила название системы уравнений Лотки-Вольтерры.