Расчетно-графические работы
По прикладной механике
Методические указания и задания
Составители: В. И. Тарханов,
Р. М. Садриев
Ульяновск
УДК 665.765:629.892(076)
ББК 39.33-08я7
Р24
Рецензент д-р. техн. наук, проф. И. Ф. Дьяков
Одобрены секцией методических пособий научно-методического совета
университета
Расчетно-графические работы по прикладной механике: методические
Р24 указания и задания / сост. В. И. Тарханов, Р. М. Садриев. – Ульяновск: УлГТУ, 2008. – 37 с.
Методические указания и задания составлены в соответствии с учебной программой по прикладной механике и предназначены для студентов энергетического и вечернего факультетов. Изложена методика выполнения расчетно-графических работ по разделу «Сопротивление материалов», которая иллюстрируется числовыми примерами.
Работа подготовлена на кафедре «Основы проектирования машин» УлГТУ.
УДК 665.765: 629.892(076)
ББК 39.33-08я7
Ó Тарханов В. И., Садриев Р. М., сост. 2008
Ó Оформление. УлГТУ, 2008
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Задание на расчетно-графические работы с указанием их объема и сроков выполнения выдается студентам на первом занятии.
Выполнение расчетно-графических работ способствует закреплению и углублению знаний, полученных на лекциях и практических занятиях, а также развитию навыков решения задач сопротивления материалов. Приведенные примеры способствуют освоению методов и приемов расчета типичных, наиболее часто встречающихся прикладных задач. При этом необходимо использовать одну из книг, приведенных в списке литературы.
Расчетно-графические работы выполняют на сброшюрованных листах белой бумаги формата А4 (297×210 мм). Чертежи, схемы и графики наносят карандашом с применением чертежных инструментов, расчеты и пояснения выполняются Microsoft Word. Шрифт – Times New Roman размером 14 pt. Междустрочный интервал – одинарный. Не допускается применять сокращения слов, кроме установленных правилами русской орфографии. При выполнении расчета сначала записывают формулу в буквенных обозначениях. Далее, вместо символов в формулу подставляют их численные значения в согласованных размерностях и в той последовательности, в которой они приведены в формуле. Затем записывают результаты вычислений с указанием размерности. Не допускается при вычислении сокращать подставленные в формулу численные значения. Иллюстрации, сопровождающие расчеты, располагают в тексте. Расчетную схему со всеми относящимися к ней эпюрами размещают на отдельном листе с соблюдением масштабов, изображаемых физических величин.
В конце расчетно-графической работы приводят библиографический список.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
Задача 1
Для определения продольных сил применим метод сечений для каждого участка стержня, при этом неизвестную внутреннюю силу N предварительно направим от сечения, предполагая ее положительной. При построении эпюры нормальных напряжений 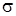 величину напряжения подсчитаем для всех участков стержня. Продольное перемещение
величину напряжения подсчитаем для всех участков стержня. Продольное перемещение 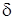 сечения находим как алгебраическую сумму удлинений
сечения находим как алгебраическую сумму удлинений 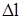 участков стержня между заделкой и рассматриваемым сечением, суммирование ведем по всем участкам.
участков стержня между заделкой и рассматриваемым сечением, суммирование ведем по всем участкам.
Пример 1
Ступенчатый стержень нагружен силами, направленными вдоль его оси. Материал стержня – сталь с модулем продольной упругости Е =  МПа. Длины участков a = 0,4 м, b = 0,5 м, c = 0,6 м. Площади поперечного сечения
МПа. Длины участков a = 0,4 м, b = 0,5 м, c = 0,6 м. Площади поперечного сечения 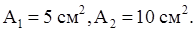 Силы F1 = 60 кН, F2 = 80 кН, F3 = 60 кН.
Силы F1 = 60 кН, F2 = 80 кН, F3 = 60 кН.
Построить эпюры продольных сил N, нормаль напряжений 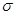 и
и
продольных перемещений 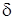 сечений стержня.
сечений стержня.
РЕШЕНИЕ
1. Продольные силы:
на участке а: 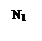





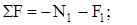

на участке b: 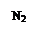
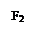
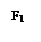






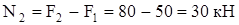
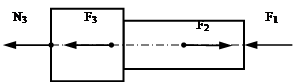 на участке c:
на участке c:
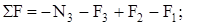
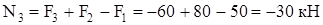
2. Нормальные напряжения:
на участке a: 
на участке b: 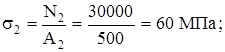
на участке c: 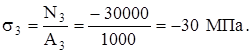
3. Продольные перемещения сечений стержня:
на расстоянии с от заделки:

на расстоянии (c+b) от заделки: 
на расстоянии (c+b+a) от заделки:
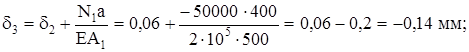
|
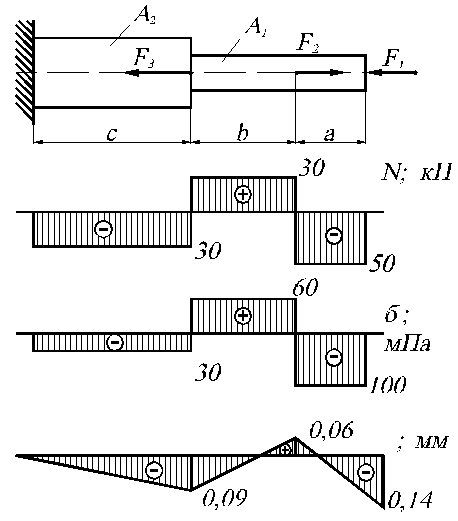







Задача 2
Стержневая система один раз статически неопределима, так как для нахождения двух неизвестных сил в стержнях можно составить лишь одно уравнение равновесия жесткого бруса. Необходимо составить дополнительно одно уравнение перемещений. Для этого сопоставим положение жесткого бруса до и после нагружения. Непосредственно из чертежа установим зависимость между удлинениями стержней.
Пример 2
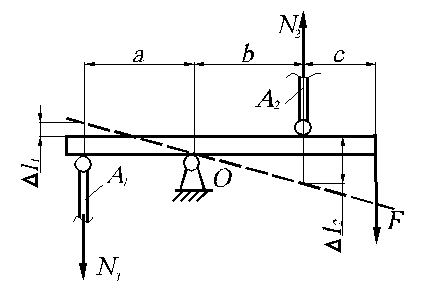
Абсолютно жесткий брус опирается на шарнирно неподвижную опору О и поддерживается двумя стержнями, прикрепленными шарнирно. Длины участка бруса a = 2 м, b = 1,5 м, c = 1 м. Длины стержней l1 = 2 м, 12 = 1,2 м. Площади поперечного сечения стержней А1 = 100 мм2, А2 = 60 мм2. Определить продольные силы и нормальные напряжения в стержнях от действия на брус силы F = 8 кН без учета веса.
РЕШЕНИЕ
1. Разрезаем стержни ивводим продольные силы N1 и N2, направляя их от сечений. Приравнивая нулю сумму моментов сил относительно шарнира О, получаем
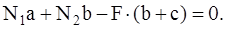 (1)
(1)

2. Под действием силы F брус поворачивается относительно шарнира О и стержни удлиняются на величину 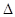 l1 и
l1 и 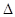 l2. Из подобия треугольников получаем соотношение:
l2. Из подобия треугольников получаем соотношение:
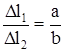 ,
,
откуда уравнение перемещений принимает вид

Подставляя значения
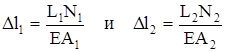
в уравнение перемещений, имеем
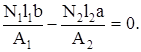 (2)
(2)
3. Продольные силы в стержнях находим из совместного решения уравнений (1) и (2). Из уравнений (2) получаем
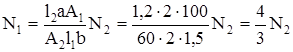
и, подставляя N1 в уравнение (1), имеем

тогда

4. Нормальные напряжения в стержнях
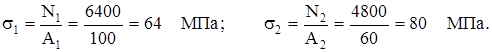
Задача 3
При построении эпюры крутящих моментов Тк применим метод сечений последовательно для всех участков вала, прикладывая неизвестный крутящий момент в положительном направлении. Диаметр вала определяем понаибольшему (абсолютному) значению крутящего момента. Угол поворота 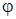 сечения определяем как алгебраическую сумму углов закручивания участков вала между заделкой и рассматриваемым сечением, суммирование ведем поучасткам с постоянными крутящими моментами.
сечения определяем как алгебраическую сумму углов закручивания участков вала между заделкой и рассматриваемым сечением, суммирование ведем поучасткам с постоянными крутящими моментами.
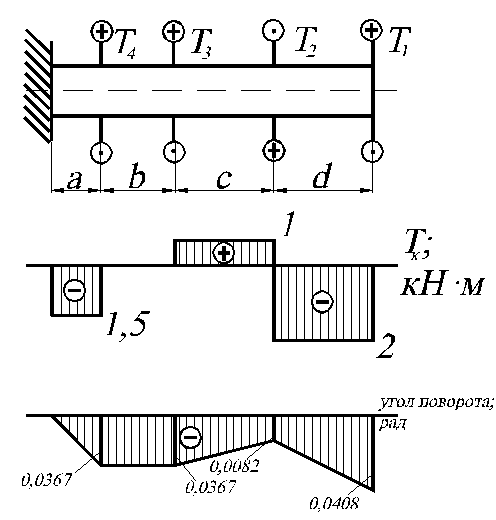
Пример 3
К стальному валу круглого сечения приложены крутящие момен
ты Т1 = 2 кН·м, Т2 = 3 кН·м, Т3 = 1 кН·м, Т4 = 1,5 кН·м. Длины
участков а = 1,2 м, b = 1,3 м, с = 1,4 м, d = 0,8 м.
Модуль сдвига стали G = 8·104 МПа. Требуется:
1) построить, эпюру крутящих моментов Тк;
2) при значении допускаемого касательного напряжения [τ] = 85 МПа
определить диаметр вала D из расчета на прочность по наибольшему
крутящему моменту; округлить величину D до ближайшего большего
значения, оканчивающегося на 0 или 5 мм;
3
) построить эпюру углов поворота φ сечений вала относительно
заделки.
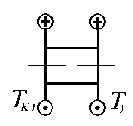 РЕШЕНИЕ
РЕШЕНИЕ
1. Крутящие моменты:
– на участке d



– на участке c
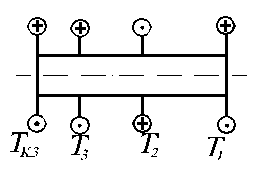

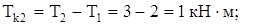
– на участке b

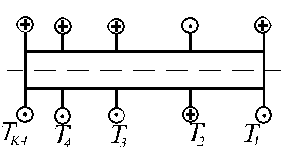 – на участке a
– на участке a

2. Диаметр вала из расчета на прочность по наибольшему крутящему моменту Т=2 кН·м.
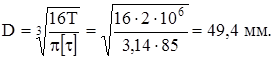
Принимаем D = 50 мм.
3. Углы поворота сечений вала:
на расстоянии a от заделки
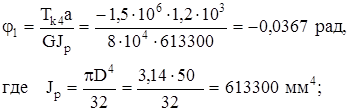
на расстоянии (a+b) от заделки
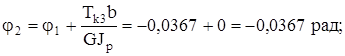
на расстоянии (a+b+c) от заделки

на расстоянии (a+b+c+d) от заделки
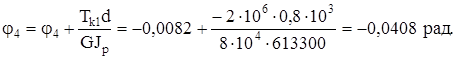
Задача 4
Реакции опор определяем, приравнивая нулю сумму моментов всех
сил относительно каждой опоры. При правильном решении сумма всех сил
равна нулю. Поперечные силы и изгибающие моменты находим по методу
сечений с учетом правил знаков. Поперечная сила в сечении балки считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – в противоположном случае. Изгибающий момент в сечении балки считается положительным, если равнодействующий момент внешних сил слева от
сечения направлен по часовой стрелке, а справа – против часовой стрелки, и отрицательным – в противоположном случае.
Для проверки правильности эпюр используем закономерности: производная от поперечной силы представляет собой внешнюю распределенную загрузку q, а производная от изгибающего момента дает поперечную силу.-
Размеры указанных сечений определяем по наибольшему (абсолют-
ному) значению изгибающего момента, при этом размеры и характеристики двутаврового сечения выбираем из таблицы сортамента прокатной
стали (приложения в учебниках [1, 2]).
На основе сопоставления площадей поперечных сечений можно сделать выводы о рациональной форме сечения балки, выгодной с точки
зрения затрат материала.
Максимальные касательные напряжения для указанных сечений подсчитываем по формуле Журавского.
Пример 4
Балка с участками длиной а = 2,5 м, b = 2 м, с = 1,5 м нагружена распределенной нагрузкой q = 20 кН/м, сосредоточенной силой F = 30 кН и сосредоточенным изгибающим моментом М = 40 кН·м.
Требуется:
1) определить реакции опор и построить эпюры поперечных сил Q и
изгибающих моментов М;
2) при значении допускаемого нормального напряжения [σ] = 150 МПа по
максимальному изгибающему моменту определить размеры двутаврового
квадратного и круглого сечений;
3) зачертить сечения c в одном масштабе;
4) сравнить площади сечений с наименьшей площадью;
5) определить максимальные касательные напряжения для трех указанных сечений.
РЕШЕНИЕ

1. Реакции опор
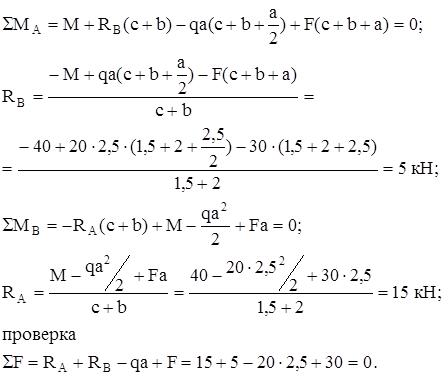
2. Эпюра поперечных сил:
на участке c суммируем силы слева от сечения: Q1=RA=15 кН;
на участке b суммируем силы слева от сечения: Q2=RA=15 кН;
на участке a суммируем силы справа от сечения: 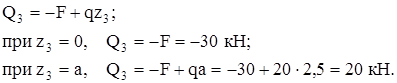
3. Эпюра изгибающих моментов:
на участке c суммируем моменты сил слева от сечения
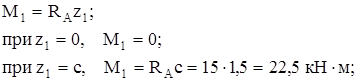
на участке b суммируем моменты сил слева от сечения
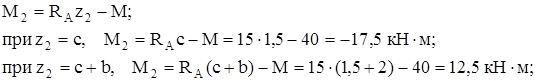
на участке a суммируем моменты сил справа от сечения 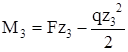 и результаты расчетов сводим в таблицу,
и результаты расчетов сводим в таблицу,
| z3 | 0,25 a | 0,5 a | 0,75 a | a | l | |
| M3 | 14,84 | 21,87 | 21,1 | 12,5 | 22,5 |
где l – координата z3 сечения, в котором Q=0 и, следовательно, производная от изгибающего момента равная нулю 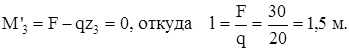
4. Момент сопротивления при изгибе максимальным моментом М = 22,5 кН·м. 
По таблице сортамента выбираем двутаровое сечение №18а, у которого Wx = 159 см3, Jx = 1430 см4, Sx*=89,8 см3, А = 6,4 см2, h = 180 мм, b = 100 мм,
d = 5,1 мм, t = 8,3 мм.