С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ.
Пусть даны два ряда с положительными членами
 (1.18)
(1.18)
 . (1.19)
. (1.19)
Теорема 1. Если для рядов с положительными членами  (по крайней мере, начиная с некоторого номера) и ряд (1.19) сходится, то ряд (1.18) также сходится.
(по крайней мере, начиная с некоторого номера) и ряд (1.19) сходится, то ряд (1.18) также сходится.
Теорема 2. Если для рядов с положительными членами  (по крайней мере, начиная с некоторого номера) и ряд (1.19) расходится, то ряд также расходится.
(по крайней мере, начиная с некоторого номера) и ряд (1.19) расходится, то ряд также расходится.
Теорема 3. Если для рядов с положительными членами существует конечный, отличный от нуля предел

то оба ряда или одновременно сходятся, или одновременно расходятся.
Докажем одну из этих теорем, например, теорему 1.
Обозначим  частичные суммы рядов (1.8) и (1.9) соответственно. Поскольку конечное число членов ряда на его сходимость не влияет, то будем считать, что неравенство
частичные суммы рядов (1.8) и (1.9) соответственно. Поскольку конечное число членов ряда на его сходимость не влияет, то будем считать, что неравенство  справедливо при всех n. Тогда
справедливо при всех n. Тогда  при всех n. Последовательности
при всех n. Последовательности 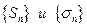 является монотонно возрастающими, т.к.
является монотонно возрастающими, т.к.  Поскольку ряд (1.9) сходится, то существует
Поскольку ряд (1.9) сходится, то существует  при этом
при этом  а потому и
а потому и 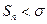 при всех n. Таким образом, последовательность
при всех n. Таким образом, последовательность  является монотонно возрастающей и ограниченной сверху, поэтому по теореме Ветештрасса существует конечный предел
является монотонно возрастающей и ограниченной сверху, поэтому по теореме Ветештрасса существует конечный предел  и, следовательно, ряд (1.8) сходится.
и, следовательно, ряд (1.8) сходится.
Примеры исследования сходимости числовых рядов с помощью теорем сравнения будут рассмотрены ниже.
ПРИЗНАК ДАЛАМБЕРА.
Теорема. Если для ряда (1.1) с положительными членами ( ), существует предел
), существует предел

то: 1) при 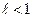 - ряд сходится; 2) при
- ряд сходится; 2) при  - ряд расходится; 3) при
- ряд расходится; 3) при 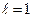 - неопределенность (в этом случае теорема на вопрос о сходимости или расходимости ряда ответа не дает и нужно применять другой признак).
- неопределенность (в этом случае теорема на вопрос о сходимости или расходимости ряда ответа не дает и нужно применять другой признак).
Доказательство. 1) Пусть 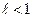 . Выберем число q, удовлетворяющее неравенству
. Выберем число q, удовлетворяющее неравенству  Обозначим
Обозначим  По определению предела последовательности для выбранного
По определению предела последовательности для выбранного  существует такой номер N, что при всех
существует такой номер N, что при всех  выполняется неравенство
выполняется неравенство
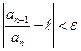
или
 .
.
Таким образом, при всех  справедливо неравенство
справедливо неравенство  В частности, при
В частности, при  получим
получим  :
:
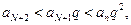
при  :
:

и т. д.
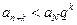
Наряду с рядом (1.1) рассмотрим ряд
 (1.10)
(1.10)
Этот ряд является геометрическим со знаменателем 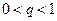 , поэтому сходится. Члены ряда (1.1), начиная с номера
, поэтому сходится. Члены ряда (1.1), начиная с номера  , меньше соответствующих членов ряда (1.10) и, следовательно, по теореме сравнения ряд (1.1) сходится.
, меньше соответствующих членов ряда (1.10) и, следовательно, по теореме сравнения ряд (1.1) сходится.
2) При  начиная с некоторого номера
начиная с некоторого номера  , будет выполнять неравенство
, будет выполнять неравенство

т.е. члены ряда монотонно возрастают. Так как рассматриваемый ряд является знакоположительным, то предел общего члена ряда при  не может быть равен 0 и поэтому ряд расходится.
не может быть равен 0 и поэтому ряд расходится.
Замечание. Признак Даламбера целесообразно использовать, когда общий член ряда содержит показательную функцию, факториалы или n сомножителей.
Пример 1. Исследовать сходимость ряда
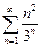 (1.11)
(1.11)
Здесь 
Тогда 
Так как  по признаку Даламбера ряд (1.11) сходится.
по признаку Даламбера ряд (1.11) сходится.
Пример 2. Исследовать сходимость ряда.
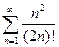 (1.12)
(1.12)
Здесь

Поскольку 
То 
Поэтому по признаку Даламбера ряд (1.12) сходится.
Пример 3. Исследовать сходимость ряда
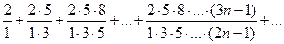 (1.13)
(1.13)
Каждый следующий член ряда получается из предыдущего путём добавления по одному сомножителю в числителе и знаменателе т.к.

то
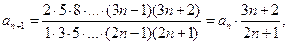
поэтому

следовательно, по признаку Даламбера ряд (1.13) расходится.
РАДИКАЛЬНЫЙ ПРИЗНАК КОШИ.
Теорема. Если для ряда с положительными членами (1.1), существует предел

то: 1) при 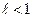 -ряд сходится; 2) при
-ряд сходится; 2) при  - ряд расходится; 3) при
- ряд расходится; 3) при 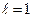 - неопределенность.
- неопределенность.
Пример 1. Исследовать сходимость ряда.
 (1.14)
(1.14)
Здесь 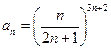 . Тогда
. Тогда

поэтому по радикальному признаку Коши ряд (1.14) сходится.
Пример 2. Исследовать сходимость рада.
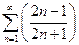 (1.15)
(1.15)
Будем использовать радикальный признак Коши.
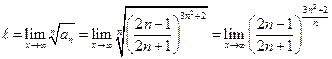
Получим неопределенность  . Сведем этот предел ко второму замечательному пределу
. Сведем этот предел ко второму замечательному пределу

Выполняя преобразования, получим
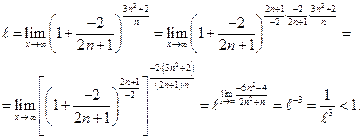
Ряд расходится.
- ИНТЕГРАЛЬНЫЙ ПРИЗНАК КОШИ.
Теорема. Пусть для ряда с положительными членами

члены ряда не возрастают, т.е.

и пусть  непрерывная не возрастающая функция такая, что
непрерывная не возрастающая функция такая, что  . Тогда, если не собственный интеграл
. Тогда, если не собственный интеграл  , сходится, то и ряд сходится; если этот несобственный интеграл расходится, то и ряд расходится.
, сходится, то и ряд сходится; если этот несобственный интеграл расходится, то и ряд расходится.
Следствие. Поскольку несобственный интеграл  сходится при
сходится при  и расходится при
и расходится при  , то ряд
, то ряд
 (1.16)
(1.16)
сходятся, если  и расходятся, если
и расходятся, если  . Ряд (1.16) называется рядом Дирихле или обобщенным гармоническим рядом.
. Ряд (1.16) называется рядом Дирихле или обобщенным гармоническим рядом.
При 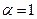 получаем ряд
получаем ряд 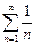 , который называется гармоническим. Выше использовалось, что этот ряд расходится.
, который называется гармоническим. Выше использовалось, что этот ряд расходится.
Пример 1. Исследовать сходимость ряда.
 (1.17)
(1.17)
(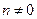 , почему?).
, почему?).
 Легко убедится, что члены ряда монотонно убывают
Легко убедится, что члены ряда монотонно убывают

Функция  непрерывная и монотонно убывающая при
непрерывная и монотонно убывающая при  . Исследуем сходимость несобственного интеграла
. Исследуем сходимость несобственного интеграла
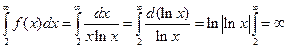
Т.к. несобственный интеграл расходится, то и ряд (1.17) расходится.
Пример 2. Исследовать сходимость ряда.
 (1.18)
(1.18)
Поскольку последовательности 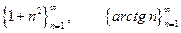 монотонно возрастающее, то члены ряда (1.15) монотонно убывают
монотонно возрастающее, то члены ряда (1.15) монотонно убывают

Функция  непрерывно и монотонно убывает при
непрерывно и монотонно убывает при  . Вычислим несобственный интеграл от этой функции:
. Вычислим несобственный интеграл от этой функции:
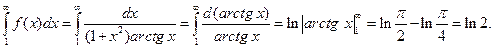
Так как несобственный интеграл сходится, то и ряд (1.18) сходится.
- ИССЛЕДОВАНИЕ СХОДИМОСТИ РЯДОВ