И ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ РЯДОВ.

Ряд, членами которого являются функции, называются функциональными.

(2.1)

Представляя вместо х какое-либо число , то получим числовой ряд. Если этот числовой ряд сходится, то называется точкой сходимости функционального ряда. Множество точек сходимости функционального ряда называется областью сходимости.

Пример 1. Найти область сходимости ряда.

(2.2)

При фиксированном х ряд (2.2) является геометрическим со знаменателем , поэтому ряд сходится, если , и расходится, если .

Область сходимости ряда – интервал .

Пример 2. Найти область сходимости ряда.

(2.3)

При 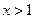ряд (2.3) сходится абсолютно, при ряд сходится условно.

Пример 3. Найти область сходимости ряда.

(2.4)

Ряд сходится, если Область сходимости ряда (2.4) – бесконечный интервал .

Функциональный ряд (2.1) называется равномерно сходящимся на отрезке [a, b], если для любого сколько угодно малого существует номер 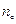такой, что при всех выполняется неравенство для всех . Здесь - остаточный член ряда: .

Функциональный ряд (2.1) называется мажорируемым на отрезке [a,b], если существует такой сходящийся числовой ряд с положительными членами, что для всех имеет место неравенство

Пример 4. Доказать, что функциональный ряд

(2.5)

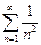мажорируем на всей числовой оси. Поскольку при всех и числовой ряд сходится, то функциональный ряд мажорируем при .

Эффективным признаком для доказательства равномерной сходимости функционального ряда является

Теорема Вейерштрасса. Если функциональный ряд мажорируем на отрезке [a,b], то он равномерно расходится на этом отрезке.

Доказательство. Пусть функциональный ряд (2.1) можорируется на отрезке [a,b] числовым рядом . Обозначим частичную сумму функционального ряда, - частичную сумму числового ряда. Т.к. этот числовой ряд сходится, то , а поэтому по определению предела для любого существует число 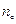такое, что при всех выполняется неравенство . Поскольку функциональный ряд мажорируем на отрезке [a,b], то при всех 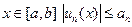, поэтому

при всех и при всех , следовательно, ряд (2.1)равномерно сходится.

Замечание. Так как ряд (2.6) мажорируем на всей числовой оси, то на основании теоремы Вейерштрасса он равномерно сходится на всей числовой оси.

Сумма функционального ряда допускает представление в виде Отсюда поэтому, если функциональный ряд сходится равномерно на отрезке для всех и всех n, начиная с некоторого номера 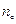. Это означает, что, начиная с некоторого номера 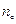, графики всех частичных сумм попадут в - коридор функции .

Теорема. (о непрерывности суммы функционального ряда). Если функциональный ряд (2.1), составленный из непрерывных функций на некотором отрезке [a,b], равномерно сходится, то его сумма является непрерывной функций на этом отрезке.

Замечание. Если нарушается условие равномерной сходимости, то сумма ряда составленная из непрерывных функций, на некотором отрезке, может оказаться разрывной функцией на этом отрезке.

Пример 5. Рассмотрим функциональный ряд.

(2.6)

Члены этого ряда являются непрерывными функциями на отрезке Найдём частичные сумму ряда.

Поскольку то сумма ряда

не является непрерывной функцией на отрезке . Она имеет разрыв в точке .

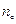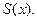Причиной этого является то, что функциональный ряд не является равномерно сходящимся на отрезке . Если построить графики частичных сумм , то не существует такого номера , чтобы начиная с него графики частичных сумм попадали в - коридор суммы (см. рис.2.2).

Теорема. 2. (о почленном интегрировании функционального ряда). Если функциональный ряд (2.1) составленный из непрерывных функций на отрезке , равномерно расходится, то интеграл от суммы ряда по любому отрезку 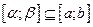равен сумме интегралов от членов этого ряда

Теорема 3. (о почленном дифференцировании функционального ряда). Если функциональный ряд (2.1), составленный из функций, имеющие непрерывные производные на отрезке [a,b], сходится к функции , а ряд, составленный из производных этих функций , равномерно сходится на этом отрезке, то производная суммы ряда равна сумме производных членов этого ряда.

СТЕПЕННЫЕ РЯДЫ.

Функциональный ряд вида

(2.7.)

называется степенным. Числа называется коэффициентом степенного ряда.

Теорема Абеля. Если степенной ряд сходится в некоторой точке , то абсолютно сходится при всех x, удовлетворяющих неравенству . Если степенной ряд расходится при всех х, удовлетворяющих неравенству

Следствие. Для степенного ряда (2.7) существует такое число , что при всех ряд сходится, притом абсолютно, а при всех расходится. К называется радиусом сходимости степенью ряда, а интервал (-R, R) – интервалом сходимости. При для исследования сходимости ряда проводится дополнительные исследования.

Радиус сходимости степенного ряда можно находить по одной из следующих формул:

(2.8)

Пример 1. Найти область сходимости степенного ряда.

. (2.9)

Здесь . Тогда и

(-1; 1) – интервал сходимости степенного ряда (2.9) Исследуем сходимость ряда (2.9) на концах интервала.

При получаем ряд , который расходится. При получаем знакочередующийся ряд , который сходится условно. Итак область сходимости ряда (2.8)

Пример 2. Найти область сходимости ряда.

(2.9)

В данном примере . Тогда

следовательно, ряд (2.9) сходится на всей числовой оси.

Пример 3. Найти область сходимости степенного ряда.

(2.10)

Здесь . Найдем радиус сходимости

(-1;1) – интервал сходимости ряда. При х = 1 ряд (2.10) принимает вид (2.11)

Так как

То ряд (2.11) расходится. При х = -1 получаем ряд и предел общего члена не существует, поэтому ряд тоже расходится. Таким образом, областью сходимости ряда (2.10) является интервал (-1;1). Ряд вида называется степенным рядом по степеням . Радиус сходимости этого ряда также можно находить по формулам (2.8), интервалом сходимости является интервал , симметричный относительно точки .

Пример 4. Найти область сходимости ряда.

(2.12)

В этом примере . Тогда

Интервалом сходимости ряда (2.12) является интервал (-1;5). Исследуем сходимость ряда (2.12) на концах интервала: При х = 5 ряд (2.12) принимает вид , является гармоническим и расходится. При х = - 1 ряд (2.12) принимает вид . Этот ряд – знакочередующийся. Используя признак Лейбница, можно доказать, что он сходится. Этот ряд сходится условно. Итак, областью сходимости ряда (2.12) является полуинтервал .

Если ряд по степеням или содержатся только четные или нечетные степени, то для нахождения области сходимости можно либо делать замену, либо непосредственно использовать признак Даламбера или интегральный признак Коши.

Пример 5. Найти область сходимости ряда.

(2.13)

В результате замены ряд принимает вид

(2.14)

Найдём радиус сходимости последнего ряда. Для него .

Тогда Итак, при ряд (2.14) сходится, а поэтому ряд (2.12) сходится, если т. е. . Исследуем сходимость ряда (2.13) на концах этого интервала. При х = 5 и при х = 1 получаем ряд , который сходится. Таким образом, областью сходимости ряда (2.13) является отрезок [1;5].

Пример 6. Найти область сходимости ряда.

(2.15)

Общий член ряда имеет вид . Тогда . Применим признак Даламбера

По признаку Даламбера ряд сходится, если и расходится, если

Таким образом, ряд (2.15) сходится, если Исследуем сходимость ряда (2.15) на концах этого интервала. При х = -3 полечим ряд , который совпадает с рядом (1.14), где показано, что он расходится. При х = -5 ряд (2.15) принимает вид и он тоже расходится. Итак, областью сходимости ряда (2.15) является интервал (-5;-3).

ДЕЙСТВИЕ НАД СТЕПЕННЫМИ РЯДАМИ.

Теорема 1. Степенной ряд (2.7) равномерно сходится на любом отрезке целиком принадлежащем интервалу сходимости степенного ряда.

Доказательство. Пусть радиус сходимости степенного ряда (2.7) равен R. Тогда на основании теоремы Абеля степенной ряд сходятся абсолютно при всех . Пусть Числовой ряд с положительными членами.

сходится, а поэтому степенной ряд (2.7) при всех является мажорируемым, следовательно, на основании теоремы Вейершьрасса ряд (1.7) равномерно сходится на отрезке .

Поскольку члены степенного ряда являются непрерывными функциями на всей числовой оси и на отрезке , при , степенной равномерно сходится, то на основании теорем для функциональных рядов общего вида получаем следующие свойства степенных рядов:

Свойство 1. На любом отрезке, целиком лежащем внутри интервала сходимости, сумма степенного ряда является непрерывной функцией.

Свойство 2. Если пределы интегрирования лежат внутри интервала сходимости, то интеграл от суммы степенного ряда равен сумме интегралов от членов этого ряда.

Свойство 3. Сумма степенного ряда является функцией, которая внутри интервала сходимости имеет производные любого порядка, каждая из которых есть сумма ряда, получающегося в результате полученного дифференцирования степенного ряда соответствующее число раз.

Для доказательства свойства 3 достаточно доказать, что при почленном дифференцировании степенного ряда его радиус сходимости не изменяется.

Пусть R – радиус сходимости степенного ряда (2.7), т.е.

Рассмотрим ряд, полученный почленным дифференцированием ряда (2.7)

Найдём радиус сходимости этого ряда.

т.е. в результате полученного дифференцирования радиус сходимости не изменился. По индукции это свойство доказывается для ряда, составленного из производных любого порядка.

Пример 7. Найти сумму ряда.

Радиус сходимости этого ряда равен 1 (проверить самостоятельно). Обозначим сумму этого ряда . Заметим, что . При ряд сходится равномерно и поэтому его можно почленно дифференцировать:

Последний ряд является геометрическим со знаменателем , поэтому при

Отсюда

Так как то с = 0, поэтому при

Пример 8. Найти сумму ряда.

(2.16)

Проверить самостоятельно, что радиус сходимости этого ряда равен 1. Обозначим сумму ряда . Так как ряд равномерно сходится при 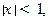то его можно почленно интегрировать при этих значения х, поэтому