С помощью теорем сравнения.

Пример 1. Исследовать сходимость ряда.

(1.19)

В этом примере . Сравним исходный ряд с рядом Дирихле который сходится, т.к. показатель Здесь .

Так как то по теореме 3 ряд (1.19) сходится.

Пример 2. Исследовать сходимость ряда.

(1.20)

Здесь Сравним исходный ряд с рядом (1.21)

Поскольку

При всех n и ряд (1.21) сходится, как ряд Дирихле с показателем , то по первой теореме сравнения ряд (1.20) сходится.

Пример 3. Исследовать сходимость ряда.

(1.22)

Так как при всех (интуитивно в этом можно убедится, сравнивая графики функций Для строгого обоснования этого неравенства можно рассмотреть функцию и с использованием производных доказать, что наибольшее значение, равное , функция достигает при . Таким образом при всех , откуда следует нужное неравенство), то для всех , поэтому

Поскольку ряд расходится, то по теореме 2 ряд (1.22) расходится.

При применении теорем сравнения часто приходится использовать эквивалентность бесконечно малых. Напомнить таблицу эквивалентных бесконечно малых при :

Пример 4. Исследовать сходимость ряда.

(1.23)

Сравним этот ряд с рядом , являющимся рядом Дирихле с показателем и поэтому расходящимся. Поскольку

то по третьей теореме сравнения ряд (1.23) расходится.

Пример 5. Исследовать сходимость ряда.

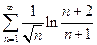(1.24)

Так как

то

Ряд с общим членом 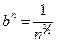сходится, поэтому по теореме (1.24) также сходится.

ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ.

ПРИЗНАК ЛЕЙБНИЦА.

Определение. Ряд вида

(1.25)

называется знакочередующимся.

Теорема. (Признак Лейбница) Если в знакочередующимся ряде (1.25) абсолютные величины членов ряда не возрастают, т.е.

(1.26)

то общий член ряда стремится к нулю, т.е.

(1.27)

то ряд сходится, его сумма не отрицательна и превосходит первого члена ряда.

Доказательство. Рассмотрим частичную сумму четного числа слагаемых, т.е. Так как сумма является конечной, то слагаемые можно сгруппировать произвольным образом. Запишем сначала частичную сумму в виде

(1.28)

В силу (1.26) каждая скобка неотрицательна, поэтому Перепишем сумму иначе:

Опять в силу (1.26) получим, что Из (1.28) следует, что последовательность является неубывающей. В тоже время она ограничена сверху, поэтому по теореме Вейерштрасса имеет предел

(1.29)

причём .

Однако отсюда не следует, что существует предел

Например, для последовательность , а последовательность предела не имеет.

Для того, чтобы доказать, что достаточно вместе (1.29) показать, что . Действительно,

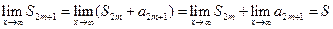
Последний предел равен нулю в силу (1.27). Таким образом, мы доказали, что Следовательно, ряд (1.25) сходится и при этом . Теорема доказана.

Пример 1. Исследовать сходимость ряда.

(1.30)

В этом случае 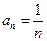. Легко убедится, что абсолютные величины членов ряда монотонно убывают

и , поэтому по признаку Лейбница ряд (1.30) сходится.

Замечание. Требование монотонности в теореме Лейбница существенно, т.е., если общий член ряда при , то не монотонно, то ряд может расходится.

Пример 2. Рассмотрим ряд.

(1.31)

Запишем частичную сумму :

Так как эта сумма конечная, то справедливы коммутативный и ассоциальный законы, т.е. слагаемые можно произвольным образом переставлять и группировать, поэтому частичную сумму можно предоставить в виде:

В первой скобке стоит n-ая частичная сумма 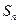гармонического ряда, который расходится, поэтому при ; во второй скобке стоит частичная сумма геометрического ряда со знаменателем поэтому