ПОНЯТИЕ ПРОИЗВОДНОЙ.
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Историческая справка.
Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики.
Великий французский математик Пьер Ферма в 1629 г. Научился находить касательные к алгебраическим прямым.
В 1638г Ферма поделился этим открытием со своим земляком Рене Декартом, который тоже занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.
Ферма далеко продвинулся в применении дифференциальных методов. Он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей.
Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему. Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в основу нового метода математического анализа – дифференциального исчисления.
«Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники».
Основоположниками этого метода считаются Вильгельм Лейбниц (1646 – 1716) и Исаак Ньютон (1642 – 1727).
Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время.
И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г. Лейбниц использовал понятие бесконечно малой.
С помощью дифференциального исчисления был решен целый ряд задач теоретической механики, физики и астрономии. В частности, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века.
|
|
Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления. Среди них – Джеймс Грегори, Якоб Бернулли, Гийом Франсуа Лопиталь, Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, который в 1797 г. ввел термин «производная» и современные обозначения y´, f´.
В настоящее время понятие производной находит большое применение в логистике и коммерческой деятельности. Умение применять производную к исследованию функции – важный элемент математической культуры.
И сейчас мы постараемся дойти до самой сути определения производной и покажем ее применение в различных областях знаний.
Сегодня у нас будет встречаться много новых терминов. «Производная» – это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это производная курицы. Понятие производной довольно трудное, т.к. основано на абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной жизни.
Мы едем из Амвросиевки до Ростова (240 км). Рассмотрим график этого движения. На оси абсцисс – время t, по оси ординат – пройденный путь s(t). На весь путь ушло 4 часа. Как узнать, с какой скоростью мы ехали. (Пройденный путь разделить на время 240: 4 = 60 км/ч)
- Мы всё время ехали с такой скоростью? (Нет, в течение пути она менялась, могла быть и больше 60 и меньше).
- Так какую скорость мы получим? (Среднюю).
- Рассмотрим участок времени Δt (пусть с 10 до 11 часов). За это время мы проехали отрезок пути Δs (пусть 40 км). С какой скоростью мы проехали этот отрезок пути? (40: 1 = 40 км/ч или Δs: Δt).
|
|
- Какая скорость получится? (Средняя) Vср. = Δs: Δt
- Если мы уменьшим отрезок времени до 0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость отслеживается с помощью радара. В момент пересечения луча радара автомобилем на табло радара высвечивается цифры скорости. Будет ли она равна средней скорости (может да, а может, нет). Как можно назвать такую скорость (мгновенной), т.к. мы рассматриваем скорость в какое-то мгновение.
Если отрезок времени стремится к 0, скорость из средней превращается в мгновенную:

Вот мы подошли к понятию производной пути.
Производная пути – это мгновенная скорость. Vмгнов. = S´(t)
- Где мы можем увидеть значение мгновенной скорости? (Радар, спидометр).
- Можем мы увидеть значение средней скорости? (Нет, её можно вычислить)
Перейдем от конкретной ситуации к любой математической функции f(x) по той же схеме.
f´(x) = lim 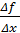 , где Δx – приращение аргумента, Δf – приращение функции.
, где Δx – приращение аргумента, Δf – приращение функции.
Определение производной.
Производной функции y = f(x) в данной точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю.
Обозначение производной: 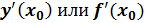 .
.
- Где в жизни применяется понятие производной? В физике – это скорость, ускорение, работа; в математике – это исследование различных функций при практических расчетах в автомобилестроении, судостроении, электронике и т.д.
Операция вычисления производной называется дифференцированием.
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
|
|
| Карточка 1 | Карточка 2 | Карточка 3 | Карточка 4 |
Для данной функции найдите предел отношения приращения функции к приращению аргумента при Δx 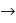 0 0
| |||
| у = –3х + 1 | у = 5х + 1 | у = –4х – 1 | у = 7х – 2 |
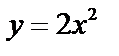
| 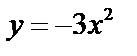
| 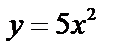
| 
|

| 
| 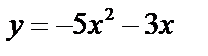
| 
|
II. Решение упражнений.
1. По определению найти производную функции:
а) у = 3х2 – 4х + 5 в точке х0 = 2, в) у = х – 2х3,
б) у = х3 + 3х2, г) у = 4х3 + 5х2 – 7х – 4.
2. Тело, масса которого m = 5 кг, движется прямолинейно по закону s = l – t + t2. Найти кинетическую энергию тела через 10 с после начала движения.
3. Самостоятельно.
| Вариант 1 | Вариант 2 |
| 1. По определению найти производную функции: | |
| а) у = 5х, | а) у = 2х, |
| б) у = 2х – 1, | б) у = 3х + 2, |
| в) у = -3х3 + 2, | в) у = 3 – 2 х3, |
| г) у = 2х3– 3х2 + 5х – 3. | г) у = 4х2– 3х3 + 5 – 3х. |