Если ряд  сходится, то
сходится, то  .
.
Следует помнить, что данный признак не является достаточным!!!
Примером служит тот же гармонический ряд - расходящийся, как только что выяснили, но для которого  .
.
Пример 4.
Ряд  расходится по необходимому признаку, так как
расходится по необходимому признаку, так как  .
.
Ряды с положительными членами.
Существует довольно много приёмов, позволяющих устанавливать сходимость или расходимость рядов - они называются признаками сходимости. К числу признаков сходимости можно отнести теоремы, сводящие выяснение вопроса о сходимости некоторого ряда к сравнению его с другим рядом, поведение которого уже известно.
Эти теоремы называются признаками сравнения.
В этом разделе будут рассматриваться только ряды с положительными членами.
Первый признак сравнения.
Пусть два ряда  и
и  таковы, что члены первого, начиная с некоторого номера, не превосходят соответствующих членов второго:
таковы, что члены первого, начиная с некоторого номера, не превосходят соответствующих членов второго:

Тогда из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда  следует расходимость ряда
следует расходимость ряда  .
.
Пример 5.
Рассмотрим ряд  . Сравним его с уже известным нам расходящимся гармоническим рядом
. Сравним его с уже известным нам расходящимся гармоническим рядом  .
.
 . Значит, и наш ряд расходится по признаку
. Значит, и наш ряд расходится по признаку
сравнения.
Пример 6.
Рассмотрим ряд  . Для выяснения вопроса о его сходимости сравним его с рядом
. Для выяснения вопроса о его сходимости сравним его с рядом  - это рассмотренная нами выше сумма геометрической прогрессии (см. Пример 1).
- это рассмотренная нами выше сумма геометрической прогрессии (см. Пример 1).
В данном случае все члены нашего ряда не превосходят членов сходящегося ряда, и множитель n в знаменателе только «усиливает» сходимость:  .
.
Также необходимо помнить, что ничего нельзя сказать о сходимости ряда, все члены которого не превосходят членов расходящегося ряда, так и о сходимости ряда, все члены которого превосходят члены сходящегося ряда.
|
|
Например, члены рядов  и
и  меньше членов расходящегося гармонического ряда
меньше членов расходящегося гармонического ряда  , однако ряд
, однако ряд  является расходящимся, а ряд
является расходящимся, а ряд  - сходящимся!
- сходящимся!
Второй признак сравнения.
Если даны два ряда  и
и  , и выполняется соотношение
, и выполняется соотношение
 , то
, то  и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7.
Ряд 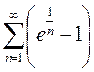 «ведёт себя» подобно гармоническому ряду а именно, расходится, так как
«ведёт себя» подобно гармоническому ряду а именно, расходится, так как  .
.
В качестве рядов, используемых для сравнения, чаще всего применяются ряды вида  (их называют рядами Дирихле) и
(их называют рядами Дирихле) и 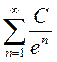 , где С – постоянная или ограниченная величина.
, где С – постоянная или ограниченная величина.
Изучить их поведение попробуем с помощью
Интегрального признака сравнения Коши.
Пусть дан ряд  , и каждый его член можно представить в виде значения какой-нибудь функции f от номера члена:
, и каждый его член можно представить в виде значения какой-нибудь функции f от номера члена:  .
.
Доопределив данную функцию для всех x на интервале [1;∞), можно говорить о непрерывной функции f(x) на интервале [1;∞), а также о существовании несобственного интеграла 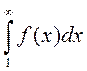 .
.
Итак, если дан ряд  , члены которого положительны и не
, члены которого положительны и не
возрастают, дана функция f(x), определённая на интервале [1;∞),
непрерывная и невозрастающая на нём и  ,тогда для сходимости ряда
,тогда для сходимости ряда 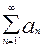 необходимо и достаточно, чтобы сходился интеграл
необходимо и достаточно, чтобы сходился интеграл  .
.
Пример 8.
Рассмотрим поведение рядов Дирихле  в зависимости от p.
в зависимости от p.
Для них f(x)=  . В этом случае
. В этом случае 
Для случая p=1 f(x)=1/x
 - интеграл расходится, что ещё раз доказывает расходимость гармонического ряда.
- интеграл расходится, что ещё раз доказывает расходимость гармонического ряда.
Итак, ряды вида  сходятся при p>1 и расходятся при p<1 и при p=1.
сходятся при p>1 и расходятся при p<1 и при p=1.
Пример 9.

В данном случае можно применить признак сравнения с рядом Дирихле после преобразования общего члена ряда с помощью формул Тейлора. Напомним их:
|
|




С помощью формулы (5) получим:

С помощью формулы (4) можем получить:

Тогда
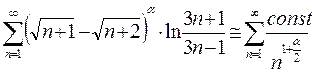
Имеем ряд Дирихле  , где p=1+
, где p=1+  . Такой ряд сходится при p>1, то есть при
. Такой ряд сходится при p>1, то есть при  >0, и расходится при p≤1, то есть при
>0, и расходится при p≤1, то есть при  ≤0.
≤0.
Пример 10. Ряд  .
.
Применим интегральный признак: f(x)=  , несобственный интеграл
, несобственный интеграл  сходится. Следовательно, сходится и ряд
сходится. Следовательно, сходится и ряд  .
.
Пример 11. Ряд  .
.
Случай p=1. f(x)=  . Применяем интегральный признак:
. Применяем интегральный признак:  - несобственный интеграл, а, вместе с ним и ряд расходятся.
- несобственный интеграл, а, вместе с ним и ряд расходятся.
Случай p≠1:

 .
.
Вместе с соответствующим несобственным интегралом, в зависимости от p, ряд  сходится при p>1 и расходится при p≤1.
сходится при p>1 и расходится при p≤1.
Необходимо отметить ещё один момент: множество сходящихся рядов образуют линейное пространство. Этим тоже можно пользоваться для установления сходимости рядов. А именно: если исследуемый ряд может быть представлен в виде конечной линейной комбинации сходящихся рядов, то он сходится.
Пример 12.  . Так как
. Так как  и каждый из рядов
и каждый из рядов 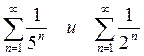 сходятся (см. пример 1), то и ряд
сходятся (см. пример 1), то и ряд  сходится.
сходится.
Если исходный ряд может быть представлен в виде линейной комбинации сходящегося и расходящегося рядов, то он расходится.
Пример 13.
Рассмотрим ряд  . Так как
. Так как  , ряд
, ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  расходится.
расходится.
Множество всех расходящихся рядов не образуют линейное пространство! Поэтому их конечные линейные комбинации могут образовывать как сходящийся, так и расходящийся ряд.
Пример 14.
Рассмотрим ряд  .
.
 . Ряды
. Ряды 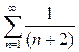 и
и  расходятся, однако исходный ряд сходится!
расходятся, однако исходный ряд сходится!
Докажем это двумя способами:
|
|
Во-первых (по признаку сравнения),  , следовательно, наш ряд сходится вместе с рядом Дирихле
, следовательно, наш ряд сходится вместе с рядом Дирихле  , С=1, p=2.
, С=1, p=2.
Во-вторых, попробуем получить частичную сумму данного ряда, чтобы доказать сходимость по определению – через предел частичных сумм. Так как  , то
, то 
 . Предел частичной суммы существует, конечен, следовательно, ряд
. Предел частичной суммы существует, конечен, следовательно, ряд  сходится по определению.
сходится по определению.
Признак Даламбера.
Пусть дан ряд с положительными членами  ,
,  , тогда, если
, тогда, если  , то ряд сходится,
, то ряд сходится,
если 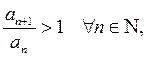 и в частности, если
и в частности, если  , то ряд расходится.
, то ряд расходится.
Если q=1, необходимо применить другой признак, так как при q=1 признак Даламбера не даёт ответа на вопрос о сходимости ряда.
Признак Даламбера удобнее всех прочих применять в том случае, если в выражении  члена ряда содержится знак факториала.
члена ряда содержится знак факториала.
Пример 15.  .
.
По признаку Даламбера:


Пример 16.

По признаку Даламбера:
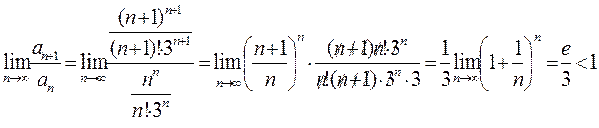 - ряд сходится.
- ряд сходится.
Отметим, что полученное соотношение  указывает на невыполнение необходимого признака сходимости ряда
указывает на невыполнение необходимого признака сходимости ряда
 .
.