Пусть дан ряд с неотрицательными членами:  ,
,  .
.
Тогда если  , то ряд сходится,
, то ряд сходится,
если  , то ряд расходится.
, то ряд расходится.
Если же  , то признак Коши не является информативным для данного случая, необходимо применить другой признак.
, то признак Коши не является информативным для данного случая, необходимо применить другой признак.
Пример 17.
 .
.
Применим признак Коши: 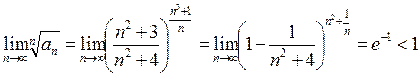 ряд сходится.
ряд сходится.
Пример 18. 
В зависимости от чётности n при  последовательность
последовательность 
будет иметь два частичных предела. Поэтому:  ,
,
ряд сходится.
Пример 19.
 .
.
Для начала применим признак Даламбера.

Как видно, этот признак не работает. В таких случаях следует применять
Признак Гаусса.
Если  и существует такое число ε>0, такое что
и существует такое число ε>0, такое что

то ряд  сходится, если μ<-1, и расходится, если μ≥-1.
сходится, если μ<-1, и расходится, если μ≥-1.
Продолжим рассмотрение примера 18.Применим признак Гаусса:

Как видно, μ=-1/2>-1 - следовательно, ряд расходится.
Для закрепления приведем ещё примеры:
Пример 20.
 . Преобразуем общий член ряда с помощью формул Тейлора, чтобы применить признак сравнения. Также нам понадобится формула
. Преобразуем общий член ряда с помощью формул Тейлора, чтобы применить признак сравнения. Также нам понадобится формула  .
.


Получили для сравнения ряд Дирихле  , который сходится при q>1 и расходится при q≤1.
, который сходится при q>1 и расходится при q≤1.
Пример 21.
 .
.
Применим признак Даламбера:
 .
.
Признак Даламбера не информативен – применим признак Гаусса:
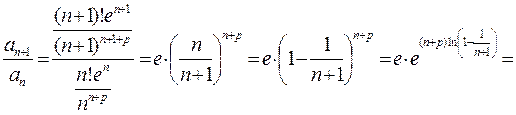

Таким образом, μ=1/2-p, то есть, данный ряд сходится при р>3/2 и расходится при p≤3/2.
При решении данного примера были использованы стандартные разложения Тейлора в степенной ряд для функций ln(1+x) и  ,а также известная из школьного курса формула
,а также известная из школьного курса формула
 была применена для преобразования вида
была применена для преобразования вида
 .(В нашем случае
.(В нашем случае  ).
).
Пример 22.

Признак Даламбера не даёт информации о сходимости ряда:
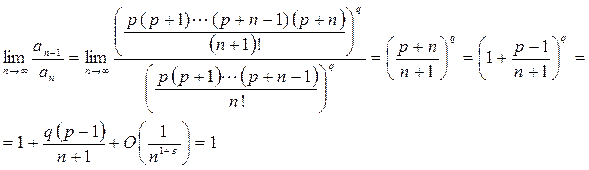
Применим признак Гаусса: 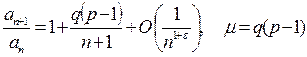
Следовательно, ряд сходится,если  и расходится, если
и расходится, если 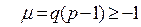 .
.
|
|
Ряды с членами произвольного знака.
Знакопеременным называется ряд, членами которого являются действительные числа произвольного знака.
Определение. Знакопеременный ряд (а также ряд с комплексными членами) называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
Для исследования рядов на абсолютную сходимость, очевидно, надо пользоваться признаками сходимости рядов с положительными членами.
Определение. Знакопеременный ряд (а также ряд с комплексными членами) называется условно сходящимся, если он сходится, но не сходится абсолютно.
Перечислим основные теоремы для знакопеременных рядов:
Теорема 1. Всякий абсолютно сходящийся ряд сходится.
Теорема 2. Если 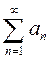 - абсолютно сходящийся ряд с суммой s, а сумма ряда
- абсолютно сходящийся ряд с суммой s, а сумма ряда 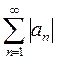 равна S, то | s|≤S.
равна S, то | s|≤S.
Теорема 3. Если в абсолютно сходящемся ряде произвольным образом переставить члены, то полученный ряд также будет сходиться, а сумма его будет равна сумме исходного ряда.
Признаки сходимости знакопеременных рядов.
Признак Абеля.
Пусть дан ряд 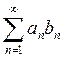 . Если последовательность
. Если последовательность  монотонна и ограничена, а ряд
монотонна и ограничена, а ряд  сходится, то ряд
сходится, то ряд  сходится.
сходится.
Признак Дирихле.
Пусть дан ряд  . Если последовательность
. Если последовательность 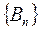 ,
,  ограничена, а последовательность
ограничена, а последовательность  монотонно стремится к нулю, то ряд
монотонно стремится к нулю, то ряд 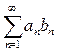 сходится.
сходится.
Определение. Знакопеременный ряд называется знакочередующимся, если соседние его члены имеют различные знаки, то есть ряд вида  .
.