Методические рекомендации
По самостоятельной работе
по изучению дисциплины «Математика и статистика»
Раздел V. Математическая статистика
Тема 5. Выборочный метод
Цель изучения – ознакомиться с основными понятиями математической статистики и возможными областями применения методов математической статистики.
Данная тема включает в себя следующие вопросы:
- цели и задачи математической статистики;
- выборочный метод: сущность и основные понятия;
- статистическое распределение выборки и формы его представления;
- эмпирическая функция распределения;
- полигон и гистограмма;
- статистическое оценивание параметров распределения (точечные и интервальные оценки);
- числовые характеристики выборки (средняя выборочная; выборочная и исправленная выборочная дисперсии; выборочное и исправленное выборочное среднее квадратическое отклонение);
- метод произведений и метод сумм нахождения числовых характеристик выборки.
Рекомендуемая литература:
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2004. – 479 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2005. – 400 с.
3. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Юнити, 2006. – 573 с.
Вопросы для самопроверки.
1. Назовите основные задачи математической статистики.
2. Дайте определения понятий: генеральная и выборочная совокупности; объем генеральной и выборочной совокупности.
3. Как обеспечивается репрезентативность выборки? Назовите основные методы отбора объектов в выборочную совокупность.
4. Укажите основные виды представления результатов выборочных наблюдений.
5. Как найти эмпирическую функцию распределения?
6. В чем отличие полигона и гистограммы распределения?
7. Приведите формулы для вычисления числовых характеристик выборки и укажите особенности их применения.
8. Назовите основные свойства точечных оценок.
9. Сравнительный анализ преимуществ и недостатков точечных и интервальных оценок.
10. Приведите формулу нахождения доверительного интервала для математического ожидания нормально распределенной случайной величины по результатам выборочных наблюдений при известном среднем квадратическом отклонении генеральной совокупности.
11. Приведите примеры использования метода сумм и метода произведений для определения числовых характеристик выборки.
Контрольные задачи по теме 5.
1. Выборка задана в виде распределения частот:
x  
| –1 | ||||
n 
|
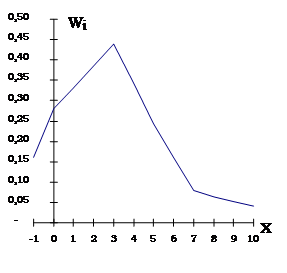
Найти: а) распределение относительных частот, б) эмпирическую функцию распределения. Построить: в) полигон частот и г) полигон относительных частот.
Отв.: а)
x  
| – 1 | 0 | 3 | 7 | 10 |
w 
| 0,16 | 0,28 | 0,44 | 0,08 | 0,04 |
 |
0 при х 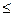 – 1
– 1
 0,16 при -1 < х
0,16 при -1 < х 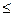 0
0
б) F 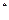 (х) = 0,44 при 0 < х
(х) = 0,44 при 0 < х 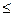 3
3
0,88 при 3 < х 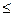 7
7
0,96 при 7 < х 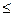 10
10
1,00 при х > 10
в) г)
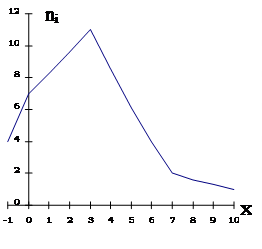
2. Результаты выборочных наблюдений над непрерывной случайной величиной X приведены ниже в виде интервалов одинаковой длины и соответствующих им частот:
x 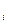 – x – x 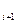
| 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
n 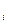
|
Построить: а) гистограмму частот и б) гистограмму относительных частот случайной величины X.
Отв.:
а) б)
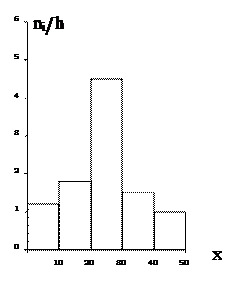
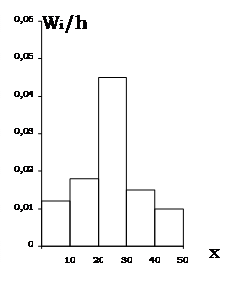
3. Найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение случайной величины X, если распределение выборки имеет следующий вид:
x  
| –5 | ||||
n 
|
Отв.: x  = 3,38; D
= 3,38; D 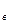
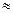 33;
33; 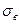
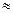 5,74.
5,74.
4. Найти несмещенные оценки генеральной средней и генеральной дисперсии, если по результатам выборочных наблюдений получено следующее распределение
x 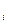 - x - x 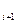
| 0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 |
n 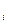
|
Отв.: x  = 20,32; S
= 20,32; S 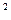 (X)
(X) 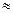 86,10.
86,10.
5. Найти интервальную оценку с доверительной вероятностью 0,95 для неизвестного математического ожидания нормально распределенной случайной величины X, если известны: генеральное среднее квадратическое отклонение
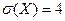 ; выборочная средняя
; выборочная средняя  x
x  = 30; объем выборки n = 25.
= 30; объем выборки n = 25.
Отв.: 28,432 < а < 31,568.
6. С помощью метода произведений найти выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение случайной величины X, если распределение выборки имеет следующий вид:
x 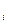 - x - x 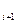
| –10 – 0 | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 |
n 
|
Отв.: x  = 25,5; D
= 25,5; D 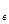 = 280,75;
= 280,75; 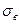
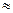 16,76.
16,76.
Тема 6. Статистическая проверка статистических гипотез
Цель изучения – ознакомиться с основными понятиями и методами статистической проверки статистических гипотез.
Данная тема включает в себя следующие вопросы:
– понятие статистической гипотезы;
– виды статистических гипотез;
– общий порядок статистической проверки статистических гипотез;
– статистические критерии;
– ошибки при статистической проверке статистических гипотез;
– проверка статистических гипотез о неизвестных параметрах известных законов распределения генеральных совокупностей:
– сравнение двух средних генеральных совокупностей;
– сравнение двух дисперсий нормальных генеральных совокупностей;
– сравнение дисперсий нескольких нормальных генеральных совокупностей;
– проверка статистических гипотез о неизвестных законах распределения генеральных совокупностей:
– проверка гипотезы о показательном распределении генеральной совокупности;
– проверка гипотезы о нормальном распределении генеральной совокупности;
– проверка гипотезы о равномерном распределении генеральной совокупности;
– проверка гипотезы о биномиальном распределении генеральной совокупности.
Рекомендуемая литература:
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2004. – 479 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2005. – 400 с.
3. Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: Юнити, 2006. – 573 с.
Вопросы для самопроверки.
1. Дайте определения статистической гипотезы, нулевой и альтернативной гипотез.
2. Почему проверка статистических гипотез называется статистической?
3. Назовите виды статистических гипотез и приведите примеры таких гипотез.
4. Какие исходы возможны при проверке статистических гипотез? Дайте определения ошибкам первого и второго родов.
5. Что называется статистическим критерием?
6. Сформулируйте понятия области принятия гипотезы и критической области. От чего зависит выбор типа критической области (левосторонней, правосторонней, двухсторонней), и как это связано с видом альтернативной гипотезы?
7. В чем заключается порядок статистической проверки статистических гипотез?
8. Что называется уровнем значимости при проверке статистических гипотез, и с какой вероятностью принимается решение?
9. Какой критерий применяется при проверке гипотезы о равенстве генеральных дисперсий двух нормальных генеральных совокупностей? Как вычисляется наблюдаемое значение этого критерия?
10. Приведите формулу для определения наблюдаемого значения критерия при сравнении средних двух нормальных генеральных совокупностей при известных генеральных дисперсиях и в случае больших независимых выборок.
11. Как проверить гипотезу о равенстве дисперсий нескольких нормально распределенных генеральных совокупностей в случае по выборкам одинакового объема? Что следует использовать в качестве оценки генеральной дисперсии, если выдвинутая гипотеза будет подтверждена?
12. В чем состоит сущность критерия Пирсона при проверке гипотезы о виде закона распределения генеральной совокупности? Приведите формулу для определения наблюдаемого значения критерия Пирсона.
13. В чем состоит отличие проверки гипотезы о виде закона распределения в случае различных законов распределения? Поясните это на примерах.
Контрольные задачи по теме 6.
1. По двум независимым выборкам, объемы которых n 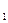 = 9 и n
= 9 и n 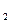 = 16, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии S
= 16, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии S 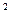 (X) = 34,02 и S
(X) = 34,02 и S 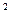 (Y) = 12,25. Проверить нулевую гипотезу H
(Y) = 12,25. Проверить нулевую гипотезу H 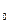 : D(X) = D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H
: D(X) = D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H 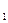 : D(X) > D(Y) и уровне значимости
: D(X) > D(Y) и уровне значимости 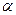 = 0,01.
= 0,01.
Отв.: Так как F 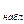 = 2,8 меньше F
= 2,8 меньше F 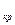 (0,01; 8; 15) = 4, то нет оснований отвергнуть нулевую гипотезу.
(0,01; 8; 15) = 4, то нет оснований отвергнуть нулевую гипотезу.
2. По двум независимым выборкам, объемы которых n 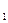 = 14 и n
= 14 и n 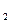 = 10, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии S
= 10, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии S 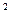 (X) =0,84 и S
(X) =0,84 и S 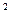 (Y) = 2,52. Проверить нулевую гипотезу H
(Y) = 2,52. Проверить нулевую гипотезу H 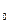 : D(X) = D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H
: D(X) = D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H 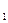 : D(X)
: D(X) 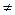 D(Y) и уровне значимости
D(Y) и уровне значимости 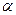 = 0,1. Отв.: Так как F
= 0,1. Отв.: Так как F 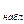 =3 больше F
=3 больше F 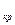 (0,05; 9; 13) = 2,72, то нулевую гипотезу отвергаем.
(0,05; 9; 13) = 2,72, то нулевую гипотезу отвергаем.
3. Четыре фасовочных автомата настроены на отвешивание одного и того же веса. На каждом автомате отвесили по 10 проб, а затем эти же пробы взвесили на точных весах и нашли по полученным отклонениям исправленные выборочные дисперсии: 0,012; 0,021; 0,025; 0,032. Можно ли при уровне значимости 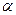 = 0,05 считать, что автоматы обеспечивают одинаковую точность взвешивания (т.е. проверить нулевую гипотезу о равенстве генеральных дисперсий), и, в случае подтверждения данной гипотезы, найти оценку генеральной дисперсии.
= 0,05 считать, что автоматы обеспечивают одинаковую точность взвешивания (т.е. проверить нулевую гипотезу о равенстве генеральных дисперсий), и, в случае подтверждения данной гипотезы, найти оценку генеральной дисперсии.
Отв.: а) так как G 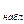 = 0,3556 меньше G
= 0,3556 меньше G 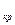 (0,05; 9; 4) = 0,5017, то можно считать, что автоматы обеспечивают одинаковую точность взвешивания; б) S
(0,05; 9; 4) = 0,5017, то можно считать, что автоматы обеспечивают одинаковую точность взвешивания; б) S 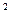 (X) = 0,0225.
(X) = 0,0225.
4. По четырем независимым выборкам, объемы которых n 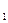 = 17, n
= 17, n 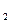 = 20, n
= 20, n 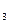 = 15, n
= 15, n 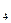 = 16, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии, соответственно равные 2,5; 3,6; 4,1; 5,8. Требуется: а) при уровне значимости
= 16, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии, соответственно равные 2,5; 3,6; 4,1; 5,8. Требуется: а) при уровне значимости 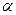 = 0,05 проверить нулевую гипотезу об однородности дисперсий; б) оценить генеральную дисперсию.
= 0,05 проверить нулевую гипотезу об однородности дисперсий; б) оценить генеральную дисперсию.
Отв.: а) k = 64; 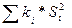 = 252,8;
= 252,8; 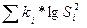 = 36,9663; V = 2,8; B
= 36,9663; V = 2,8; B 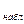 <2,8;
<2,8; 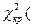 0,05; 3)=7,8; B
0,05; 3)=7,8; B 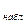 <
< 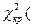 0,05; 3). Следовательно, нет оснований отвергнуть гипотезу об однородности дисперсий; б) S
0,05; 3). Следовательно, нет оснований отвергнуть гипотезу об однородности дисперсий; б) S 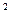 (X) = 4,00.
(X) = 4,00.
5. По выборке объемом n = 30 найден средний вес 
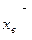 = 130 деталей, изготовленных на первом станке; по выборке объемом m = 40 найден средний вес
= 130 деталей, изготовленных на первом станке; по выборке объемом m = 40 найден средний вес  y
y 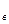 = 125 деталей, изготовленных на втором станке. Известны генеральные дисперсии D(X) = 60 г
= 125 деталей, изготовленных на втором станке. Известны генеральные дисперсии D(X) = 60 г 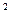 , D(Y) = 80 г
, D(Y) = 80 г 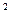 . Требуется при уровне значимости
. Требуется при уровне значимости 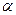 = 0,05 проверить нулевую гипотезу H
= 0,05 проверить нулевую гипотезу H 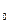 : M(X) = M(Y) о равенстве генеральных средних данных совокупностей при альтернативной гипотезе H
: M(X) = M(Y) о равенстве генеральных средних данных совокупностей при альтернативной гипотезе H 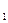 : M(X)
: M(X) 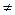 M(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.
M(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.
Отв.: Так как Z 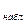 = 2,5
= 2,5  больше Z
больше Z 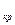 = 1,96, то нулевую гипотезу отвергаем (т.е. средний вес деталей различается значимо).
= 1,96, то нулевую гипотезу отвергаем (т.е. средний вес деталей различается значимо).
6. По выборке объемом n = 50 найден средний размер x 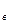 = 20,1 мм диаметра валиков, изготовленных автоматом №1; по выборке объемом m = 50 найден средний размер y
= 20,1 мм диаметра валиков, изготовленных автоматом №1; по выборке объемом m = 50 найден средний размер y  = 19.8 мм диаметра валиков, изготовленных автоматом №2. Генеральные дисперсии известны: D(X) = 1,750 мм
= 19.8 мм диаметра валиков, изготовленных автоматом №2. Генеральные дисперсии известны: D(X) = 1,750 мм 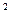 и D(Y) = 1,375 мм
и D(Y) = 1,375 мм 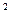 . Требуется при уровне значимости
. Требуется при уровне значимости 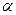 = 0,05 проверить нулевую гипотезу H
= 0,05 проверить нулевую гипотезу H 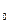 : M(X) = M(Y) о равенстве средних размеров валиков, изготовленных на данных автоматах, при альтернативной гипотезе H
: M(X) = M(Y) о равенстве средних размеров валиков, изготовленных на данных автоматах, при альтернативной гипотезе H 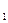 : M(X) > M(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.
: M(X) > M(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.
Отв.: Так как Z 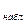 = 1,2 меньше Z
= 1,2 меньше Z  = 1,645, то нет оснований отвергать нулевую гипотезу.
= 1,645, то нет оснований отвергать нулевую гипотезу.
7. Используя критерий Пирсона, при уровне значимости 0,01, установить, случайно или значимо расхождение между эмпирическими частотами n  и теоретическими частотами n
и теоретическими частотами n 
 , вычисленными исходя из гипотезы о нормальном распределении генеральной совокупности X:
, вычисленными исходя из гипотезы о нормальном распределении генеральной совокупности X:
n  
| |||||||
n 
|
Отв.: Так как 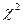
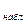 = 3,061 меньше
= 3,061 меньше 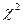
 (0,01;4) = 13,3, то расхождение между эмпирическими и теоретическими частотами является случайным и, следовательно, гипотезу о нормальном распределении генеральной совокупности X нет оснований отвергать.
(0,01;4) = 13,3, то расхождение между эмпирическими и теоретическими частотами является случайным и, следовательно, гипотезу о нормальном распределении генеральной совокупности X нет оснований отвергать.
8. Используя критерий Пирсона, при уровне значимости 0,05, проверить гипотезу о нормальном распределении генеральной совокупности X, если выборочное распределение из этой совокупности имеет следующий вид;
x  
| |||||||||
n 
|
Указание: при определении выборочной средней и выборочного среднего квадратического отклонения использовать метод произведений.
Отв.: Так как 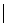
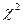
 = 22,2
= 22,2  больше
больше 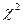
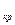 (0,05; 6) = 12,6, то нулевую гипотезу о нормальном распределении генеральной совокупности X отвергаем.
(0,05; 6) = 12,6, то нулевую гипотезу о нормальном распределении генеральной совокупности X отвергаем.
9. Используя критерий Пирсона, при уровне значимости 0,05, проверить гипотезу о нормальном распределении генеральной совокупности X, если выборочное распределение из этой совокупности имеет следующий вид;
x  - x - x 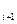
| (–20) – (–10) | (–10) – 0 | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
n 
|
Отв.: Так как 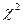
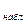 = 29,664
= 29,664  больше
больше 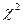
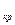 (0,05; 4) = 9,5, то нулевую гипотезу о нормальном распределении генеральной совокупности X отвергаем.
(0,05; 4) = 9,5, то нулевую гипотезу о нормальном распределении генеральной совокупности X отвергаем.
10. В итоге испытаний 1000 элементов на время безотказной работы получено эмпирическое распределение, приведенное в таблице (в верхней графе указаны интервалы времени в часах; в нижней графе – частоты n  , т. е. количество элементов, отказавших в i –м интервале).
, т. е. количество элементов, отказавших в i –м интервале).
x  - x - x 
| 0– 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 |
n 
|
Требуется при уровне значимости 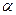 = 0,01 проверить нулевую гипотезу о том, что время безотказной работы элементов подчиняется показательному закону распределения.
= 0,01 проверить нулевую гипотезу о том, что время безотказной работы элементов подчиняется показательному закону распределения.
Отв.: Так как 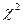
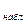 =15,88 больше
=15,88 больше 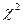
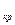 (0,01; 5) = 15,1, то нулевую гипотезу о показательном распределении времени безотказной работы X отвергаем
(0,01; 5) = 15,1, то нулевую гипотезу о показательном распределении времени безотказной работы X отвергаем
11. В некоторой местности в течении 300 суток регистрировалась среднесуточная температура воздуха. В итоге наблюдений было получено эмпирическое распределение, приведенное ниже в таблице (в первом столбце указан интервал температуры в градусах, во втором столбце – частота n 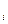 , т.е. количество дней, среднесуточная температура воздуха которых принадлежит этому интервалу).
, т.е. количество дней, среднесуточная температура воздуха которых принадлежит этому интервалу).
x  – x – x 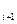
| n 
| x – x 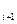
| n 
| |
| –40 – (–30) | 0 – 10 | |||
| –30 – (–20) | 10 – 20 | |||
| –20 – (–10) | 20 – 30 | |||
| –10 – 0 | 30 - 40 |
Требуется при уровне значимости 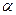 = 0,05 проверить гипотезу о том, что среднесуточная температура воздуха распределена равномерно.
= 0,05 проверить гипотезу о том, что среднесуточная температура воздуха распределена равномерно.
Отв.: Так как 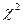
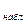 = 7,71 меньше
= 7,71 меньше 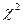
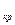 (0,05; 5) = 11,1, то нет оснований отвергать нулевую гипотезу о равномерном распределении среднесуточной температуры воздуха X.
(0,05; 5) = 11,1, то нет оснований отвергать нулевую гипотезу о равномерном распределении среднесуточной температуры воздуха X.
12. Опыт, состоящий в одновременном подбрасывании четырех монет, повторили 100 раз, эмпирическое распределение дискретной случайной величины X – числа появившихся “гербов” – оказалось следующим (в первой строке указано число x  выпавших “гербов” в одном бросании монет; во второй строке – частота n
выпавших “гербов” в одном бросании монет; во второй строке – частота n  , т.е. число бросаний, при которых выпало x
, т.е. число бросаний, при которых выпало x  “гербов”):
“гербов”):
x  
| |||||
n 
|
Требуется при уровне значимости 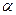 = 0,05 проверить гипотезу о том, что случайная величина X распределена по биномиальному закону.
= 0,05 проверить гипотезу о том, что случайная величина X распределена по биномиальному закону.
Указание. Принять вероятность выпадения “герба” при бросании одной монеты p = 0,5.
Отв.: Так как 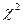
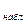 = 2,88 меньше
= 2,88 меньше 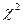
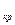 (0,05; 4) = 9,5, то нет оснований отвергать нулевую гипотезу о биномиальном распределении случайной величины X.
(0,05; 4) = 9,5, то нет оснований отвергать нулевую гипотезу о биномиальном распределении случайной величины X.
13. Отдел технического контроля проверил n = 100 партий изделий по N = 10 изделий в каждой партии и получил следующее эмпирическое распределение дискретной случайной величины X – числа нестандартных изделий (в первой строке указано число x  нестандартных изделий в одной партии; во второй строке – частота n
нестандартных изделий в одной партии; во второй строке – частота n  , т.е. количество партий, содержащих x
, т.е. количество партий, содержащих x  нестандартных изделий):
нестандартных изделий):
x  
| ||||||||
n 
|
Требуется при уровне значимости 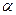 = 0,01 проверить гипотезу о том, что случайная величина X распределена по биномиальному закону.
= 0,01 проверить гипотезу о том, что случайная величина X распределена по биномиальному закону.
Указания.
1.Найти сначала относительную частоту появления нестандартных изделий (отношение числа всех нестандартных изделий к общему числу проверенных изделий) и принять ее в качестве оценки p 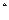 вероятности того, что наудачу взятое изделие окажется нестандартным.
вероятности того, что наудачу взятое изделие окажется нестандартным.
2.При составлении расчетной таблицы для сравнения эмпирических и теоретических частот с помощью критерия Пирсона необходимо для первых двух групп объединить эмпирические частоты (2 + 3 = 5), следовательно, число групп после объединения составит s = 7.
3.Один параметр (вероятность p) оценивался по выборке, поэтому при определении числа степеней свободы надо вычесть из s не единицу, а два: k = s – 2 = 5.
Отв.: p 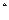 = 0,4; так как
= 0,4; так как 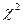
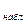 = 0,68 меньше
= 0,68 меньше 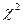
 (0,01; 5) = 15,1, то нет оснований отвергать нулевую гипотезу о биномиальном распределении случайной величины X.
(0,01; 5) = 15,1, то нет оснований отвергать нулевую гипотезу о биномиальном распределении случайной величины X.
14. В итоге проверки на нестандартность 200 ящиков консервов получено следующее эмпирическое распределение (в первой строке указано число x  нестандартных коробок консервов в одном ящике; во второй строке – частота n
нестандартных коробок консервов в одном ящике; во второй строке – частота n  , т.е. число ящиков, содержащих x
, т.е. число ящиков, содержащих x  нестандартных консервов):
нестандартных консервов):
x 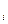 
| |||||
n 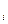
|
Требуется при уровне значимости 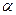 = 0,05 проверить гипотезу о том, что случайная величина X – число нестандартных коробок консервов распределена по закону Пуассона.
= 0,05 проверить гипотезу о том, что случайная величина X – число нестандартных коробок консервов распределена по закону Пуассона.
Указание. Объединить малочисленные частоты двух последних групп.
Отв.: Так как 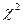
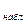 = 9,27 больше
= 9,27 больше 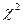
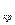 (0,05; 2) = 6,0, то нулевая гипотеза о распределении случайной величины X по закону Пуассона отвергается.
(0,05; 2) = 6,0, то нулевая гипотеза о распределении случайной величины X по закону Пуассона отвергается.
Литература
1. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. - М.: Высшая школа, 2005. – 404 с.
2. В.Е. Гмурман. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2004. – 479 с.
3. И.Ш. Кремер. Теория вероятностей и математическая статистика. – М.: Юнити, 2006. – 573 с.
 |