Любой механизм представляет собой кинематическую цепь (к.ц.) звеньев, соединенных в кинематические пары (к.п.). К.ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными.
В простой к.ц. каждое из ее звеньев входит в состав одной или двух к.п., а в сложной к.ц. имеются звенья, входящие в состав трех и более к.п.
В открытой к.ц. имеются звенья, входящие в состав одной к.п., а в замкнутой цепи каждое звено входит в состав 2-х и более к.п. (рис.6,а-в).
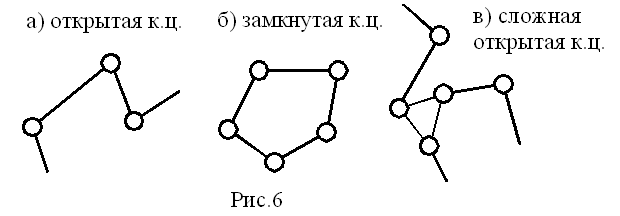
Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к.ц. называется плоской, в противном случае к.ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).
Ответ 5.
Степень подвижности механизма равна трем. Между тем движение кулисы является принужденным, а две лишние степени подвижности характеризуют способность кулисы и камня независимо вращаться вокруг общей оси ВС и не влияют на законы движения точек кулисы и ее оси. [1]
Степень подвижности механизма или число его степеней свободы соответствует тому количеству его ведущих звеньев, которое необходимо для определенности движения ведомых звеньев. Если, например, механизм обладает одной степенью подвижности, то в этом механизме должно быть одно ведущее звено. Если же степень подвижности равна трем (w 3), то механизм должен иметь три звена с заданными законами движения. [2]
Степень подвижности механизма определяется числом ведущих звеньев, законы движения которых заданы. [3]
Степенью подвижности механизма называется число независимых параметров, которое нужно задать для определения положения всех его подвижных звеньев.
Ответ №6
Класс механизма
Класс механизма определяется наивысшим классом групп Ассура, входящих в его состав.
На рисунках 8…9 приведены примеры схематического изображения групп Ассура различных классов. Пунктирными линиями изображены звенья механизма, к которым присоединяется данная группа (они не входят в состав группы).
Как было отмечено выше, простейшие группы, включающие в свой состав два звена и три кинематические пары пятого класса, относятся к группам Ассура II класса (по И.И. Артоболевскому). Все они имеют два свободных элемента кинематических, которыми присоединяются к другим звеньям механизма (на рисунке 8 – это элементы А и С), поэтому одновременно являются группами второго порядка (в связи с этим обычно о порядке групп Ассура второго класса не говорят).
Группа Ассура второго класса, имеющая в своем составе все три вращательные пары (шарниры), условно отнесена к группе первого вида. Последующие виды образуются последовательным замещением вращательных пар поступательными («ползунами»).
Заменой одной крайней вращательной пары поступательной парой образуется группа второго вида.
Замена среднего шарнира на поступательную пару образует группу третьего вида.
Группа четвертого вида получается при замене двух крайних вращательных пар на поступательные и, наконец, заменой одной крайней вращательной пары и средней пары на поступательные формируется группа пятого вида.
Для лучшего запоминания и определения вида группы при структурном анализе механизмов можно воспользоваться аббревиатурой пар, входящих в ее состав: ВВВ (вращательная-вращательная-вращательная) – группа 1 вида; ВВП (вращательная-вращательная-поступательная) – группа 2 вида; ВПВ – группа 3 вида; ПВП – группа 4 вида; ВПП – группа 5 вида.
На рисунке 8 представлены группы второго класса всех пяти видов. В верхнем ряду группы изображены в самом общем случае. Однако на практике многие размеры задаются таким образом, что конфигурация групп значительно трансформируется. Поэтому для лучшей ориентации в таблице приведены некоторые частные случаи, которые могут встретиться при анализе механизмов.
На рисунке 9 представлены примеры структурных групп более высоких классов. На рисунке представлены группы только с вращательными парами, что облегчает понимание класса и порядка групп Ассура. На самом деле в любом месте группы вместо вращательной пары может быть поставлена поступательная, что принципиально не меняет сути классификации.
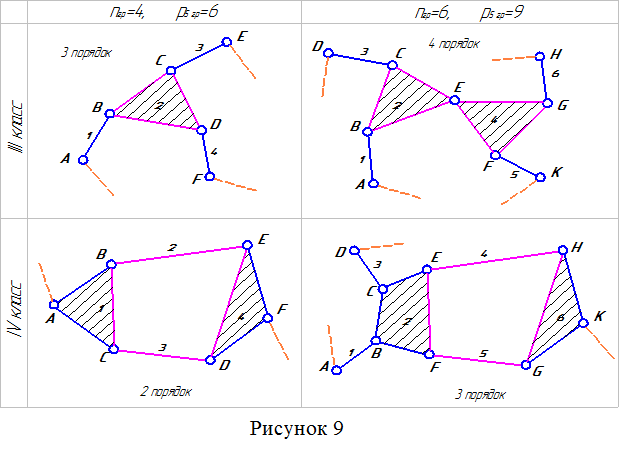Ценность структурной классификации механизмов заключается в том, что группы Ассура обладают постоянными свойствами, независимо от того в каком механизме они находятся, в какой сфере жизнедеятельности применяется данный механизм.
Это дает возможность иметь универсальные методы исследования любых механизмов через разработку методов исследования отдельных групп Ассура. Таким образом, установив класс механизма, фактически определяют порядок анализа и методы решения задач, связанных с его работой.
|
Ответ №11
Вращательная кинематическая пара образуется цапфой (опорной частью вала) и охватывающим её подшипником. Для того чтобы цапфа, находящаяся под действием нескольких приложенных к ней сил, могла вращаться, необходимо, чтобы равнодействующая Р этих сил (рис. 1) создавала момент не меньший момента силы трения.
Разложив силу Р на нормальную Рn и тангенциальную Рτ составляющие и обозначив через: r плечо действия силы Р относительно оси вращения цапфы; R – радиус цапфы; λ - угол между линией действия силы Р и радиусом, проведённым в точку приложения силы P, получим:
момент, вращающий цапфу, равен
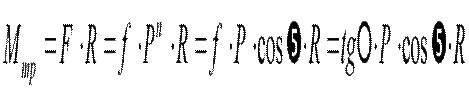
Для возможности движения необходимо соблюдение условия
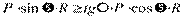, откуда
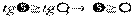, и поэтому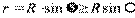 
Следовательно, момент силы Р не может вращать цапфы, если линия действия силы Р проходит внутри круга с радиусом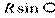 
. Такой круг получил название – круга трения.
ответ №12
Учет сил трения качения
Сопротивление движению при качении (трение качения) обусловлено эффектом молекулярного сцепления на площадке контакта, упругостью тел и трением при относительном проскальзывании поверхностей вследствие разной кривизны соприкасающихся тел.
В высшей кинематической паре, образованной звеньями 1 и 2 (рис. 1.23, а) в статическом состоянии под нагрузкой G вследствие деформации возникает площадка контакта, на которой действуют давления, распределенные по симметричному закону. При этом их равнодействующая: N = G проходит через центр катка. Для качения звена к нему необходимо приложить момент Т. Это обусловлено тем, что при перекатывании звена удельные давления перераспределяются таким образом, что общая реакция N смещается в направлении перекатывания на расстояние k, вследствие чего возникает момент сопротивления перекатыванию (рис. 1.23, б):
Ттр = k N. (1.56)
Коэффициент трения качения k = Ттр / N имеет размерность длины. Значение k определяется опытным путем. Оно зависит от упругих свойств материалов, радиуса кривизны соприкасающихся поверхностей, скорости качения и других факторов. В инженерной практике принимают: k= 0,005 … 20 мм; наименьшие значения назначают для катков высокой твердости, наибольшие – при качении резиновых шин по мягкому грунту.
Рис. 1.23. Схема сил, действующих на цилиндр
Чтобы сравнить потери мощности на преодоление сопротивлений при качении и скольжении, представим движущий момент Т в виде пары сил: F=T/R (рис. 1.23, в), т.е. будем считать, что сила F приложена к центру катка. При равномерном движении эта сила равна силе сопротивления Fс движению. Условие равенства моментов сил относительно точки контакта: FR=kN. Исходя из этого, сила сопротивления равна соотношению
Fс = F = kN/R = fпрN, (1.57)
где fпр= k/R – приведенный коэффициент трения качения. Экспериментальные исследования показали, что значение приведенного коэффициента трения качения fпр почти на два порядка меньше коэффициента f трения скольжения.
Ответ № 13
КПД механизмов соединенных последовательно.
Часто для выполнения необходимой работы в машине применяется несколько разных механизмов, соединенных между собой.
Рисунок 30
В этом случае движение (и мощность) передается последовательно от одного механизма к другому. Полезной работой для предыдущего механизма является приведение в движение следующего. То есть полезная работа на выходе предыдущего механизма является одновременно движущей для последующего. Полезной работой всей системы является работа на выходе из последнего механизма системы:
Таким образом, общий коэффициент полезного действия системы последовательно соединенных механизмов равен произведению коэффициентов полезного действия этих механизмов:
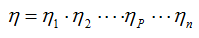
Так как КПД любого механизма меньше единицы, то КПД системы последовательно соединенных механизмов оказывается всегда ниже худшего из механизмов этой системы. Поэтому, если применяется система последовательных механизмов (или отдельных элементов), то не следует включать в эту систему механизмы с низкими КПД.
Если последовательно соединяется "n" одинаковых механизмов:
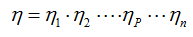
то
где ηP – КПД любого промежуточного механизма.
ОТВЕТ №14
КПД Механизмов соединенных параллельно
Параллельное соединение
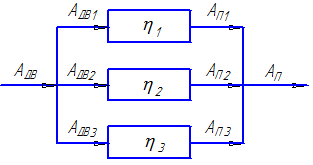
Рисунок 31
Несколько механизмов приводятся в движение одним двигателем. Полезная работа системы складывается из полезных работ на выходе из каждого механизма. На приведение в движение каждого из механизмов двигатель затрачивает часть своей энергии (АДВ i). Тогда коэффициент полезного действия такой системы можно представить следующим образом:
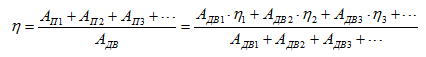
В данном случае величина общего кпд зависит от доли энергии, отдаваемой двигателем механизмам с более высокими или более низкими кпд. Но во всех случаях общий КПД занимает некоторое промежуточное значение по отношению к частным КПД механизмов, соединенных в систему (КПД системы будет тем выше, чем большая часть энергии двигателя будет отдаваться механизмам с высокими КПД).
Если параллельно соединяется "n" одинаковых механизмов:
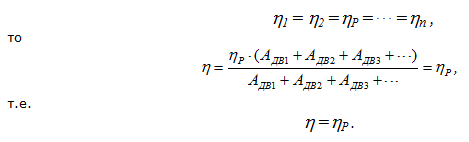
При параллельном соединении одинаковых механизмов КПД системы не изменяется и равен КПД одного механизма
Ответ №15
Переменное нагружение
Переменное нагружение связано с очень сложными явлениями.
Переменное нагружение, когда существенным является влияние концентрации напряжений на усталость металла.
Переменное нагружение торсионного вала при наличии больших динамических нагрузок обусловливает необходимость оптимизации его параметров
Переменные нагружения упругопластических тел в радиационном поле / / Динамические и технологические проблемы механики конструкций и сплошных сред: Матер.
Характерпеременного нагружения большей частью бывает синусоидальным
Припеременном нагружении, особенно с заданной деформацией, введение разгружающих надрезов может заметно повысить конструктивную прочность или увеличить число циклов до разрушения при той же нагрузке. Так, например, при знакопеременном кручении на заданный угол 7 образцов из стали ЗОХГСА после закалки и отпуска при 200 С образец с одним круговым надрезом выдерживает до разрушения восемь циклов, а образец с тремя последовательно расположенными такими же надрезами выдерживает 38 циклов.
Припеременном нагружении образца, когда напряжение изменяется по синусоидальному закону, необратимо затраченная за один цикл удельная работа деформации A rar0eosin (p тем больше, чем больше разность фаз напряжения и деформации.
Асимметричный циклпеременного нагружения детали возникает либо при несимметричном характере изменения внешней нагрузки на деталь относительно нуля, либо при наложении на симметричный цикл переменных напряжений (вибраций) статической нагрузки или комплекса нагрузок.
Впоследствии Москвитин рассмотрелпеременные нагружения в рамках общей математической теории пластичности Ильюшина.
Кривая усталости
КРИВАЯ УСТАЛОСТИ
Вёлера кривая, - графич. изображение способности материала сопротивляться усталостному разрушению (зависимость Макс. напряжения цикла от числа циклов до разрушения). Различают 2 осн. типа К. у.: 1) по достижении определ. напряжения число циклов до разрушения практически перестаёт изменяться при дальнейшем уменьшении напряжения; 2) при увеличении напряжения число циклов до разрушения непрерывно уменьшается. В зависимости от типа К. у. применяют разные способы определения предела выносливости (усталости)
Ответ №17
Растяжение и сжатие. Эпюры продольных сил
Растяжение и сжатие
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила.
Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график - эпюра продольных сил.
Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией.
Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией. Примеры построения эпюр
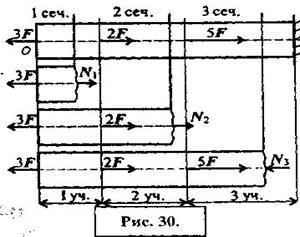
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.)
Делим брус на участки закрепления.
Участком закрепления считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Расчёт начинаем со свободного конца бруса, чтобы не определять величины реакции в опорах.
Участок 1:
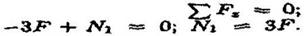
Продольная сила положительна, участок 1 растянут. Участок 2:
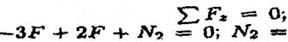
=F. Продольная сила положительна, участок 2 растянут.
Участок.'
Продольная сила отрицательна, участок з сжат. Полученное значение равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис.31.).
Эпюра продольной силы строится только под брусом.
Эпюры продольных сил
Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса.
Ось эпюры параллельна продольной оси. Нулевая линия проводится тонкой линией. Значения чисел откладывают от оси, положительные - вверх, отрицательные вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачек на величину приложенной силы.
На эпюре проставляют значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и обводится поперёк оси.
Принцип смягчения граничных условий гласит: в точках тела, удалённых от мест нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Ответ №18