Тема урока: Назначение и основные виды аксонометрических проекций.
Домашнее задание: изучить тему урока.
Построение аксонометрических проекций плоских фигур
Общие сведения. Государственный стандарт устанавливает несколько видов аксонометрических проекций. Для построения наиболее наглядных изображений применяется прямоугольная изометрическая проекция (кратко - изометрия, от греч изо - равный, одинаковый).
Положение аксонометрических осей этой проекции приведено на рисунке 1, а. Как видно из чертежа, оси проекции в изометрии располагаются под углом 120° друг к другу. При построении фигур размеры отрезков по осям х0 у0 z0 откладывают без изменения, т. е. действительные.
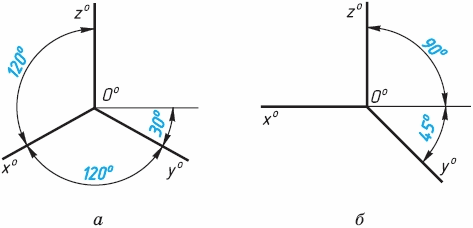
Рис. 1
В том случае, когда действительные размеры берут только по двум осям (х0, z0), проекцию называют диметрической (от греч. ди - дважды).
Положение осей диметрической проекции дано на рисунке 1, б.
Аксонометрические проекции многоугольников. Построение аксонометрических проекций начинают с проведения осей. Параллельно им откладывают размеры отрезков.
Рассмотрим построение аксонометрических проекций плоских геометрических фигур, расположенных в горизонтальной плоскости. Построения даны в изометрической проекции.
Треугольник. Симметрично точке 00 (рис. 2) по оси х0 откладывают отрезки С0А0 и 00Е0, равные половине стороны треугольника, а по оси у0 - его высоту 00С0. Полученные точки А0, B0 и С0 соединяют отрезками прямых.
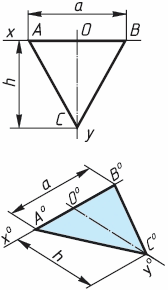
Рис. 2
Квадрат. По оси х0 от точки 00 (рис. 3) откладывают отрезок а, равный стороне квадрата, вдоль оси у0 - также отрезок а. Затем проводят отрезки, параллельные отложенным.
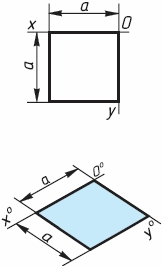
Рис. 3
Шестиугольник. По оси х0 вправо и влево от точки 00 (рис. 4) откладывают отрезки, равные стороне шестиугольника. По оси у0 симметрично точке 00 откладывают отрезки, равные половине расстояния L между противоположными сторонами шестиугольника, т. е. L/2
|
|
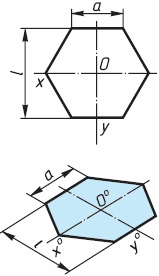
Рис. 4
Через точки, полученные на оси у0, проводят вправо и влево параллельно оси х0 отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.
Если контур фигуры сложный, то при построении аксонометрической проекции эту фигуру удобно заключить в квадрат, прямоугольник и пр. (рис. 4).
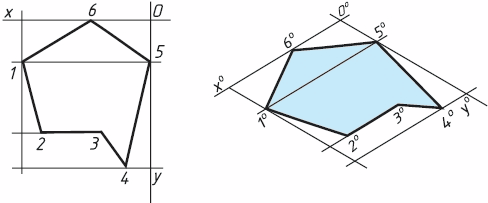
Рис. 4
Аксонометрическая проекция окружности. В аксонометрической проекции окружность в общем случае проецируется в кривую, которую называют эллипсом. Эллипс - замкнутая плоская кривая. Ее строят с помощью лекал. Поскольку строить эллипсы трудно, при изображении окружности в аксонометрии их разрешается заменять овалами. Овал - кривая, очерченная дугами окружности.
Рассмотрим построение овала, представляющего изометрическую проекцию окружности. Овал удобно строить, вписывая его в ромб, который является изометрической проекцией квадрата. Построение выполняют в следующем порядке:
1. Строят ромб, сторона которого равна диаметру изображаемой окружности. Для этого через точку 00 проводят оси х0 и у0 (рис. 5, а). На них от точки С0 откладывают отрезки С01, С02 и т. д., равные радиусу изображаемой окружности. Через точки 1, 2, 3 и 4 проводят прямые, параллельные осям х0 и у0, получая на чертеже точки A, Б, С и D.
2. Для того чтобы вписать в ромб овал, из вершин тупых углов - точек В и А - проводят дуги. Их радиус R равен расстоянию от вершин тупых углов (точек Б и A) до точек 1, 2 или 3, 4 соответственно (рис. 5, б).
|
|
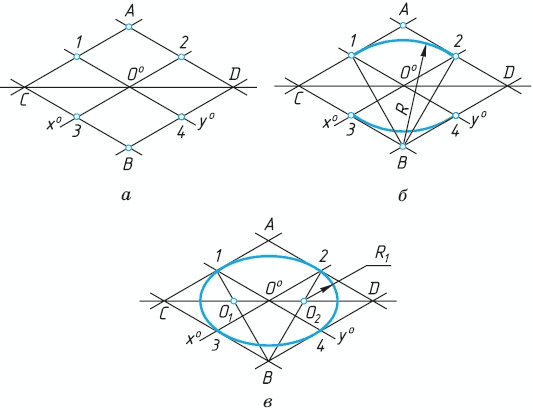
Рис. 5
3. Через точки В и 1, В и 2 проводят прямые. При пересечении прямых В1 и В2 с большей диагональю ромба CD получают точки 01 и 02 (Рис. 72, в). Эти точки будут центрами малых дуг. Их радиус R1 равен 011 (или 022). Дугами малого радиуса R1 соединяют большие дуги овала.