В произвольном базисе 
задана матрица тензора напряжения:
T= 
, МПа.
Чтобы рассчитать главные нормальные напряжения σ11, σ22, σ33 необходимо решить характеристическое уравнение 
)=0. В результате решения получаем корня уравнения λ1, 
2, 3. В соответствии с правилом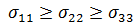 
присваиваем каждому значению -значение 
Запишем коэффициенты характеристического уравнения:
;
;
.
Подставим заданные значения и получим:
;
;
.
Подставим полученные инварианты в характеристическое уравнение 
=0. Методом подбора определяем первый корень этого уравнения 1=3.
В результате определения первого корня получаем следующее квадратное уравнение: 
=0. При нахождении корней этого уравнения получаем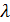 
2=8; 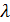3=-9. В соответствии с правилом 
получаем главные нормальные напряжения:
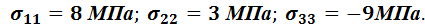
Чтобы показать направления главных нормальных напряжений, необходимо определить ориентировку элементарного параллелепипеда, построенного на векторах единичных нормалей к площадкам главных нормальных напряжений.
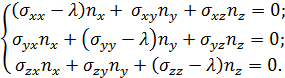
Составляем систему уравнения для λ=8:
или 
;
или 
.
После решения системы уравнения получаем 
;
Составляем систему уравнения для λ=3:
После решения системы уравнения, получаем 
)
Составляем систему уравнения для λ=-9:
В итоге решения этой системы уравнения получаем: 
– векторы единичной нормали к площадкам действия главных нормальных напряжений; 
- максимальное главное нормальное напряжение,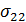 
- среднее главное нормальное напряжение;
-минимальное главное нормальное напряжение.
Рис.1
Главные касательные напряжения и ориентировка площадок главных касательных напряжений. Нормальные напряжения на площадках главных касательных напряжений
|
|
Выше были определены главные нормальные напряжения:
Среди главных касательных напряжений существует максимальное касательное напряжение 
.
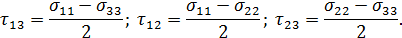
Найдём нормальные напряжения на площадках с максимальными касательным напряжениями.
Площадки максимальных касательных напряжений составляют угол ±45º с направлением главных нормальных напряжений.
Находим ориентировку площадок с максимальными касательными напряжениями из системы уравнений:
Посчитаем nk1x и nk1y для угла 45º:
Получаем: 
, 
.
Посчитаем второй случай для nk2x и nk2y:
Получаем: 
, 
Ориентировка площадок максимальных касательных напряжений
, 
– векторы единичных нормалей к площадкам максимальных касательных напряжений, – векторы единичной нормали к площадкам действия главных нормальных напряжений; - максимальное главное нормальное напряжение, 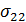- среднее главное нормальное напряжение; -минимальное главное нормальное напряжение.
Рис.2
1.3. Интенсивность касательных напряжений 
В базисе собственных векторов линейного преобразования интенсивность касательных напряжений находится по формуле[1]:
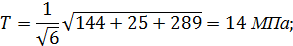
T =14 МПа;
Этот результат удовлетворяет соотношению Ильюшина 
Коэффициент Лоде
Для более полной оценки вида схемы напряжённого состояния используется коэффициент Лоде.
1.5. Компоненты девиатора напряжения. Среднее гидростатическое напряжение и показатель напряжённого состояния 
Среднее нормальное напряжение 
для базиса, совпадающего с направлением собственных векторов, равно:
|
|
Тензор напряжений Тσ можно разложить на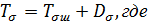 
Тσ – тензор напряжений, Тσш – шаровой тензор, Dσ – девиатор.
Представим разложение Тσ для базиса, совпадающего с направлением собственных векторов:
Интенсивность касательных напряжений: Т = 14 МПа.
Показатель напряжённого состояния: 