Лекция 4. комплексные числа
Содержание
1. Понятие комплексного числа
2. Действия над комплексными числами в алгебраической форме.
3. Геометрическая интерпретация комплексных чисел
4. Тригонометрическая форма комплексного числа.
5. Показательная форма комплексного числа.
6. Решение алгебраических уравнений в пространстве комплексных чисел.
Понятие комплексного числа
Введение комплексных чисел вызвано тем, что во множестве действительных чисел не выполнено извлечение корня четной степени из отрицательного числа. Комплексные числа являются обобщением действительных чисел.
Пример. Решить квадратное уравнение 
.
.
Мнимая единица 
определяется как число, квадрат которого равен (–1). Таки образом, 
.
Учитывая, что 
, получаем два комплексных корня:
, 
.
· Комплексным числом 
называется выражение вида 
, где 
и 
- действительные числа, а - мнимая единица.
Запись комплексного числа в виде 
называется алгебраической формой записи комплексного числа.
· Действительные числа и в алгебраической записи комплексного числа называются действительной и мнимой частямикомплексного числа и обозначаются
, 
.
Если 
, то 
, т.е. комплексное число равно действительному числу. Множество действительных чисел 
, таким образом, есть подмножество множества комплексных чисел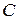 
: 
.
Если 
, то число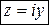 
называют чисто мнимым.
· Под модулем комплексного числа понимается неотрицательное число 
.
· Сопряженным числом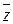 
к числу называется комплексное число 
.
Пример. Числа 
и 
- взаимно сопряженные.
Их модули равны между собой:
; 
.
Действия над комплексными числами в алгебраической форме
Введем на множестве комплексных чисел отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
· Два комплексных числа 
и 
называются равными, если равны их действительные и мнимые части:
, 
В частности, 
, 
.
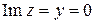Заметим, что:
1) одно равенство комплексных чисел равносильно двум равенствам и действительных чисел;
2) понятия «больше», «меньше» для комплексных чисел не определяются.
· Суммой (разностью) комплексных чисел 
и 
называется комплексное число
.
Пример. Найти сумму комплексных чисел 
и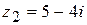 
.
Решение. 
.
Операция сложения комплексных чисел обладает свойствами:
1. 
(переместительный закон)
2. 
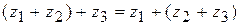(сочетательный закон)
3. 
4. Для каждого комплексного числа существует такое число , которое в сумме дает нуль: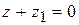 
. Оно называется противоположнымкомплексным числом для и обозначается 
. Таким образом, 
.
· Произведением комплексных чисел и называется комплексное число
.
Отсюда получаем важное соотношение:
, то есть .
Не стоит запоминать формулу умножения – правило умножения получается формально путем умножения двучленов 
и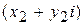 
с учетом 
.
Пример. Найти произведение комплексных чисел и .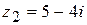
.
Операция умножения комплексных чисел обладает свойствами:
1. 
(переместительный закон)
2. 
(сочетательный закон)
3. 
(распределительный закон)
4. Произведение взаимно сопряженных комплексных чисел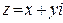 
и 
равно квадрату их модуля: 
.
· Частным от деления комплексного числа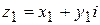 
на комплексное число (
) называется комплексное число, равное
.
Найдем действительную и мнимую части частного двух комплексных чисел. Домножим числитель и знаменатель на число 
, сопряженное знаменателю:
Сама формула громоздка и трудно запоминается. Поэтому проще умножить числитель и знаменатель дроби 
на , то есть на число, сопряженное знаменателю, и произвести преобразования.
Пример. Найти частное от деления комплексного числа на число .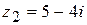
.
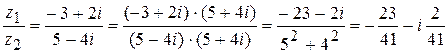