Задание
1.Получить вебер-амперную характеристику ИНЭ.
1.1.Для двух мгновенных значений тока ИНЭ i1=Im и i2=Im/4 рассчитать магнитную цепь.
Значение тока Im выбрать таким, чтобы магнитопровод при этом токе находился насыщенном состоянии:
,
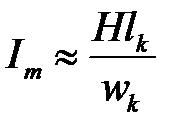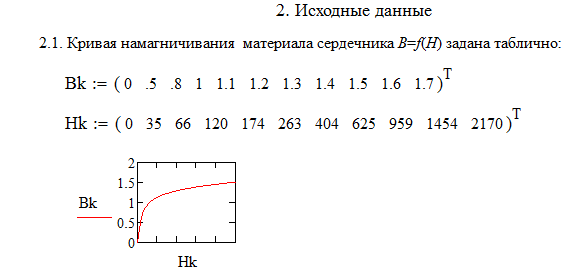
где H выбирается по ОКН в области насыщения за коленом кривой намагничивания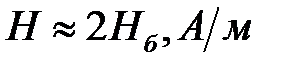 
(рис.3).
Участок аб, на котором рост магнитной индукции замедляется называемый коленом кривой намагничивания
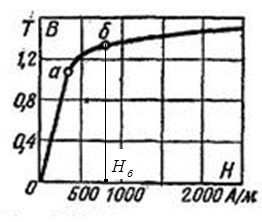
Рис.3
2.По двум рассчитанным точкам вебер-амперной характеристики определить аппроксимирующую функцию:
.
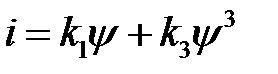Построить график зависимости 
.
3.По гармонической зависимости напряжения на ИНЭ для его четырех действующих значений U ипо зависимости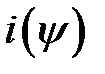 
рассчитать действующие значения гармоник тока и его действующее значение. Результаты расчета занести в таблицу. Построить ВАХ ИНЭ U(I).
4.Определить выражение мгновенного тока для заданного значения напряжения.
5.Построить на одном рисунке графики u(t), ψ(t) и i(t).
Методические указания
Расчет магнитной цепи
Формальная аналогия между электрическими и магнитными цепями позволяет распространить все методы и технику расчета нелинейных резистивных цепей постоянного тока на нелинейные магнитные цепи. При этом для наглядности можно составить эквивалентную схему замещения исходной магнитной цепи, с использованием которой выполняется расчет.
Расчет разветвленных магнитных цепей постоянного тока основанный на применении законов Кирхгофа для магнитных цепей содержит несколько этапов: 1) составление эквивалентных схем; 2) запись уравнений Кирхгофа для магнитной цепи; 3) решение полученной нелинейной системы уравнений.
Составление эквивалентной схемы
Эквивалентная схема ИНЭ с учетом варианта будет представлять собой три параллельно соединенные ветви (рис. 3).
На эквивалентной схеме показаны положительные направления магнитных потоков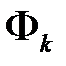 
; магнитодвижущих сил 
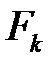; сопротивление воздушного зазора 
. Участки магнитопровода представлены нелинейными элементами с вебер-амперными характеристиками 
.
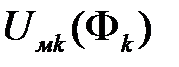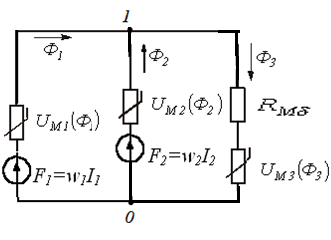
Рис.3. Схема замещения магнитной цепи
Нелинейность магнитных цепей определяется нелинейным характером зависимости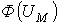 
, определяемой характеристикой ферромагнитного материала 
. При расчете магнитных цепей при постоянных потоках обычно используют ОКН.
Данный метод основан на графическом представлении вебер-амперных характеристик 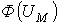линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
Замена магнитной цепи эквивалентной электрической схемой замещения позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
В этом случае при расчете магнитных цепей, содержащих два узла широко используется метод двух узлов. Идея решения данным методом аналогична для нелинейных резистивных цепей постоянного тока и заключается в следующем:
1. Вычисляются зависимости 
потоков во всех 
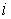-х ветвях магнитной цепи в функции общей величины - магнитного напряжения 
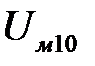между узлами 1 и 2.
2. Определяется, в какой точке графически реализуется первый закон Кирхгофа для магнитной цепи. Соответствующие данной точке потоки являются решением задачи.
Может потребоваться продолжить кривую намагничивания симметрично относительно начала координат.
Пример расчета магнитной цепи
.
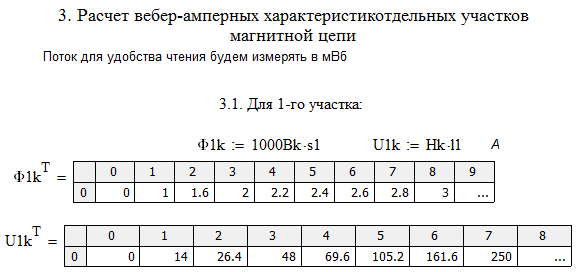
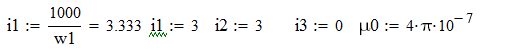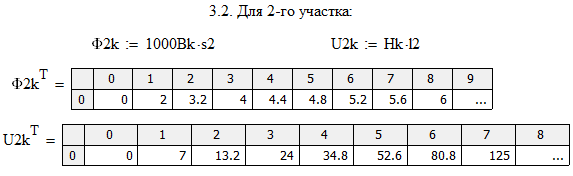
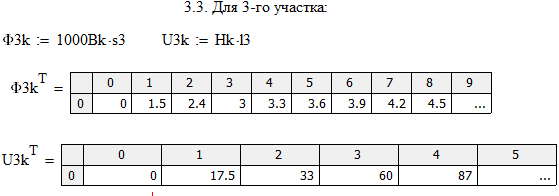
2.4.Графический расчет магнитной цепи
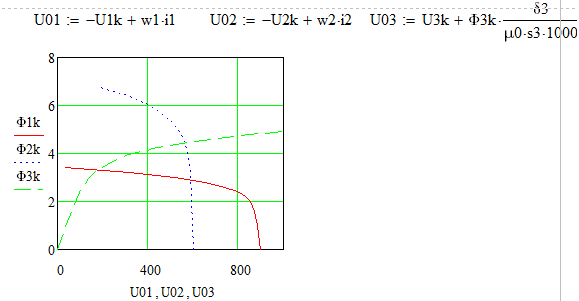
Далее следует изобразить в другом масштабе нужную часть рисунка.
Графически определяем потоки и потокосцепление:
При токе равном I = 3 А получили (рис.4): 
; 
;
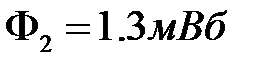=1.07 Вб.
При токе равном I =0.5 А получили: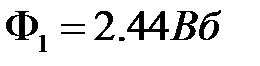 
; 
;
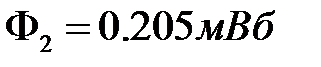=300∙0.00244+200∙0.000205=0.733 Вб.
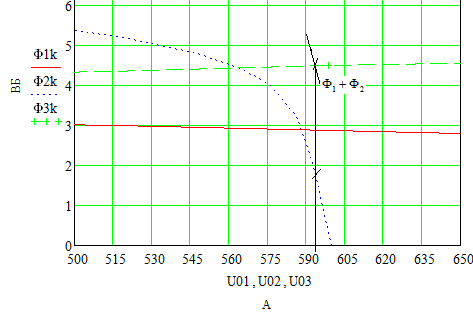
Рис.4 (i=3A)
Рис.5 (i=0.5A)
3. Аппроксимация веберамперной характеристики
Аппроксимируем характеристику неполным полиномом:
.
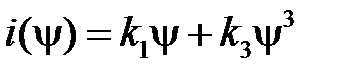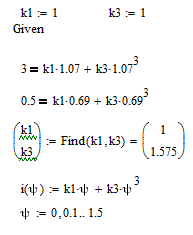
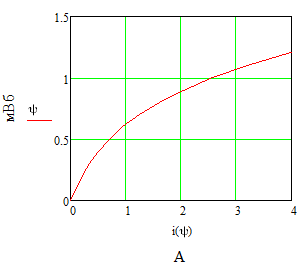
Рис.6. Веберамперная характеристика
Расчет ВАХ
⇒ 
⇒ 
; 
; 
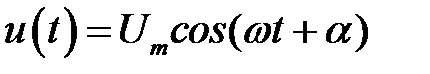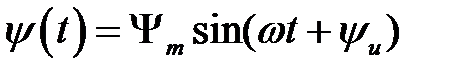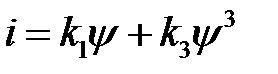
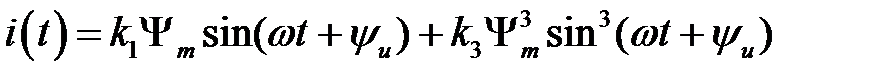
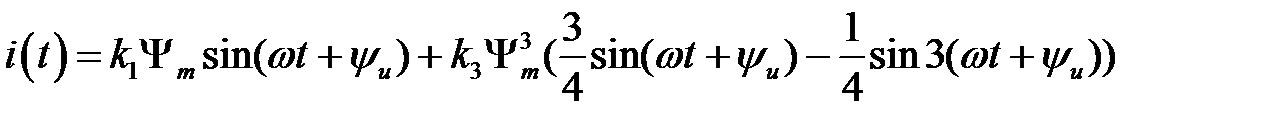
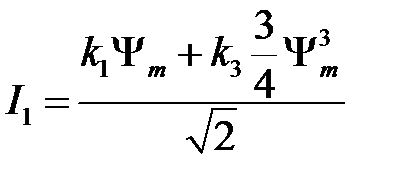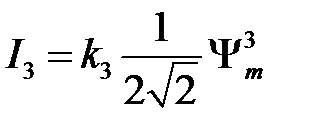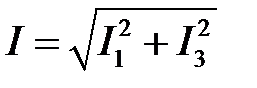
Выполнение.
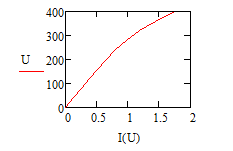
Рис.8.Вольт-амперная характеристика
5.Построение графиков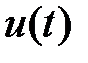 
, 
, 
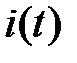для заданного напряжения.
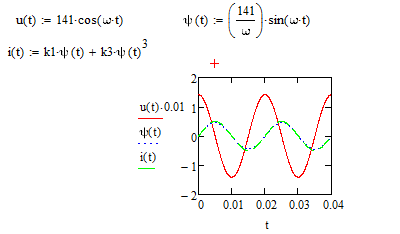
Рис.9. Графики напряжения, потокосцепления и тока