Спектрально-люминесцентные свойства гранатов, активированных ионами хрома, каскадная эмиссия фотонов в люминофорах и стереоатомный анализ

Спектр люминесценции кристаллов, активированных ионами хрома, существенно меняется от матрицы к матрице в зависимости от силы кристаллического поля. В кристаллах с сильным полем люминесценция обусловлена двукратно запрещенным переходом ²Е – ⁴А₂, спектр люминесценции представляет собой узкие слабые линии, в кристаллах со слабым полем люминесценция связана с однократно запрещенным ⁴Т₂ – ⁴А₂, спектр излучения представляет собой широкую мощную электронно-колебательную полосу. В кристаллах со средним значением силы поля спектр излучения есть суперпозиция переходов ²Е – ⁴А₂ и ⁴Т₂ – ⁴А₂. Лишь в кристаллах со средним и слабым кристаллическим полем ионы хрома демонстрируют свои выдающиеся донорные и генерационные способности. Поиск таких матриц до настоящего времени является нетривиальной задачей.

Поэтому результаты исследований люминесцентных свойств ионов хрома в гранатах обращают на себя внимание, а стереоатомный анализ их структуры и выявление связи спектральных свойств с характеристиками полиэдров Вороного-Дирихле наиболее удобными для отработки модели.

Замены ртутного разряда на Xe-разряд, обусловленна техническими, экологическими и другими причинами. Однако простая замена ртутного разряда на ксеноновый разряд невозможна, так как спектры возбуждения люминофоров, разработанных для ртутного разряда не согласуются со спектром излучения Хе-разряда, максимум полосы излучения которого приходится на 170 нм, что значительно короче длины волны ртутного разряда l = 254 нм. Это обстоятельство выдвигает более жесткие требования к люминофорам для ламп с Хе-разрядом, так как прямое преобразование одного кванта света с длиной волны 170 нм в квант видимого излучения с l » 510 нм энергетически не эффективно. Эта проблема может быть решена при реализации каскадной люминесценции.

Для наблюдения каскадной люминесценции необходимо соблюдение некоторых условий; в частности, для иона Pr^{3+ 1}S_o – уровень должен быть расположен ниже дна 5d-зоны. Так как радиальное распределение 5d-орбиталей выходит за рамки 5s²6р⁶-оболочек, в результате чего положение 5d-уровней весьма чувствительно к кристаллическому полю, т.е. к химической природе лигандов и их координации вокруг иона Pr³⁺. Данная глава посвящена выявлению закономерностей влияния химической природы лигандов и их координации вокруг иона Pr³⁺ на формирование спектров люминесценции.

 

4. Влияние структурных особенностей кристаллических гранатов, карунда и шпинели на величину энергетического зазора ΔЕ₁₃ между возбужденными состояниями ⁴Т₂ и ²Е ионов Cr³⁺

 

Из многочисленных диэлектрических материалов, используемых для возбуждения генерации СИ, соединения со структурой граната (пространственная группа О¹⁰_h – Ia 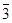d) занимают особое место – они являются самыми применяемыми в квантовой электронике [4, 5]. Спектрально-генерационные исследования этих кристаллов с общей формулой A₃B^I₂B^II₃O₁₂ были начаты в середине 60-х годов [4]. К настоящему времени перечень лазерных матриц с этой структурой уже насчитывает более тридцати наименований, генерирующими активаторами в которых служат как Ln³⁺ -ионы (Nd³⁺, Dy³⁺, Ho³⁺, Er³⁺, Tm³⁺, Yb³⁺), так и ионы группы железа (Cr³⁺, Ti³⁺, Ni²⁺).

Как известно [6], в элементарную ячейку соединений структурного типа граната входят восемь формульных единиц (всего 160 атомов). Для удобства формулу гранатов можно записать как {A₃}[B^I₂](B^II₃)O₁₂, где фигурными, квадратными и круглыми скобками выделены катионы, занимающие с -, а - и d -кристаллографические позиции соответственно. B^I-атомы занимают 16 октаэдрических а -положений (С_3i), B^II- атомы – 24 тетраэдрических d -положения (S₄); а -узлы образуют объёмно-центрированную кубическую решётку, 24 А-иона находятся в додекаэдрических (D₂) с -позициях. Структура иттрий-алюминиевого граната (ИАГ) приведена на рис. 4.1. Наиболее компактными в ИАГ являются тетраэдрические позиции с расстоянием до анионов 1,75 Å, для октаэдра это расстояние – 1,94 Å, для додекаэдра – 2,37 Å. Ионы кислорода расположены в 96 общих h -кристаллографических позициях. Додекаэдр имеет общие рёбра (связь О-О) с двумя тетраэдрами, четырьмя октаэдрами и четырьмя другими додекаэдрами. Координационные полиэдры несколько искажены: октаэдры – вдоль оси 3, а тетраэдры – вдоль оси 4; 8 анионов в додекаэдре двумя группами по 4 аниона расположены от а -узла на разных расстояниях. В элементарной ячейке имеется 8 неэквивалентных октаэдрических, 6 тетраэдрических и 6 додекаэдрических позиций [7, 8].

 

Рис. 4.1. Кристаллическая структура гранатов

 

Рентгеноструктурные и кристаллохимические исследования [9-17] свидетельствуют о том, что возможно существование чрезвычайно обширного ряда соединений со структурой граната, в которых а -, с - и d - положения могут занимать ионы различной валентности большого числа элементов (практически всех групп таблицы Менделеева). Причём некоторые из них, проявляя исключительную избирательность, могут заполнять полностью эти кристаллографические позиции, т.е. образовывать в трёхподрешёточной структуре граната свою подрешётку, которая определённым образом может оказывать влияние на катионы (например, на орбитальные моменты их валентных электронов) двух других подрешёток.

Изучение условий возбуждения стимулированного излучения (СИ) в кристаллах, активированными ионами Cr³⁺, необходимо при создании материалов для получения СИ, перестраиваемого в широкой области ИК-диапазона. Поскольку эти результаты хорошо освещены в литературе (см., например, [4, 18]), здесь будут приведены лишь некоторые важные для кристаллохимического рассмотрения выводы этих исследований.

Известно, что сила кристаллического поля уменьшается с увеличением расстояния Cr³⁺ – лиганд и уменьшением заряда лиганда. В галогенидах она, например, меньше, чем в оксидных соединениях, поэтому предлагалось использовать активированные Cr³⁺ кристаллы фторидов. Такой лазер был создан, например, на основе кристалла KZnF₃:Cr³⁺. Весьма плодотворным оказался другой путь – поиск оксидных кристаллов с максимальным расстоянием Ме-О в октаэдрах, в которые при активации входят ионы Cr³⁺, с целью уменьшения величины кристаллического поля. (Уменьшения силы поля можно достичь также в гетеродесмических кристаллических оксидах с низким эффективным зарядом кислорода. Так, в кристаллических силикатах эффективный заряд кислорода -1,1).

Расстояние Ме-О в гранатах возрастает с увеличением а₀. Исследования редкоземельных алюминиевых, галлиевых и других гранатов [4] позволили получить набор кристаллов с ионами Cr³⁺, в которых энергетический зазор между состояниями ²Е и ⁴Т₂ (рис. 4.2) ионов Cr³⁺ (он характеризует силу кристаллического поля) уменьшается от ~1300 см^-1 для ИАГ (Y₃Al₅O₁₂) приблизительно до нуля для Gd₃(Sc,Ga)₅O₁₂ и CaMg₂Y₂Ge₃O₁₂ [19].

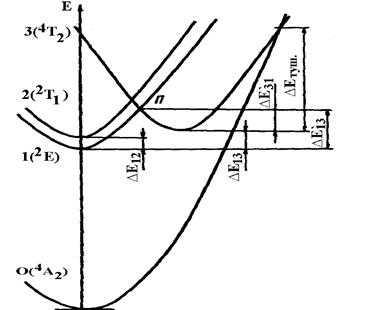
Рис. 4.2. Фрагмент схемы нижних энергетических уровней примесного иона Cr³⁺

 

Гадолиний скандий галлиевый гранат имеет большой параметр а₀=12,57 Å и в силу этого высокий коэффициент распределения К_р для Ln³⁺-ионов и, в частности, для Nd³⁺. Для ионов Cr³⁺ в этом кристалле К_р ≈1. Теплофизические свойства Gd₃(Sc,Ga)₅O₁₂ несколько хуже, чем для Y₃Al₅O₁₂ (теплопроводность в гранатах обычно падает с увеличением атомной массы катионов), однако они являются вполне удовлетворительными [19].

Авторы работ [19] провели исследование спектрально-люминесцентных и кинетических характеристик синтезированных кристаллов галлиевых гранатов с примесью ионов Cr³⁺ и установили, что спектральные свойства и донорные возможности ионов Cr³⁺ определяются в значительной степени величиной энергетического зазора ∆Е между возбужденными состояниями ⁴Т₂ и ²Е (рис. 4.2), которая, в свою очередь, зависит от симметрии и силы кристаллического поля, в котором находятся ионы Cr³⁺ , т.е. от геометрии окружения и расстояния до ближайших анионов.

Вследствие этого желаемое взаимное расположение уровней ⁴Т₂ и ²Е в принципе может быть достигнуто подбором катионов основы в пределах данной структуры. Малая величина ∆Е, сравнимая (или меньше) с kТ при

 

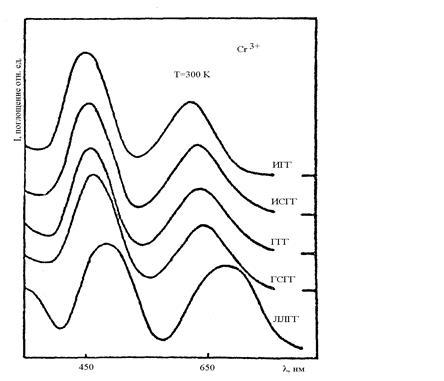
Рис. 4.3. Положение линий поглощения ионов хрома при Т=300 К

в кристаллах ИГГ (Y₃Ga₅O₁₂), ИСГГ (Y₃Sc₂Ga₃O₁₂), ГГГ (Gd₃Ga₅O₁₂), ГСГГ (Gd₃Sc₂Ga₃O₁₂) и ЛЛГГ (La_2.55Lu_2.45Ga_2.96O_11.93)

 

комнатной температуре, приводит к высокой населенности уровня ⁴Т₂, что, в свою очередь, обуславливает наличие у ионов Cr³⁺ широкополосной люминесценции, связанной с переходом ⁴Т₂ → ²Е, и высокую эффективность передачи энергии на соответствующие акцепторы благодаря активному участию в процессе передачи уровня ⁴Т₂.

На рис. 4.3 представлены спектры поглощения, а на рис. 4.4 – люминесценции ионов Cr³⁺ в синтезированных кристаллах галлиевых гранатов [19], а на рис. 4.5 спектр люминесценции YAG:Cr³⁺. Широкие полосы поглощения связаны, как известно, с переходами ⁴А₂ → ⁴Т₂ или ²Т₁, а люминесценция – с электронно-колебательным переходом ⁴Т₂ →⁴А₂.

В кристаллах ГГГ:Cr³⁺ так же, как и в ГСГГ:Cr³⁺, соотношение интенсивностей полос ⁴Т₂ → ⁴А₂ и ²Е → ⁴А₂ зависит от концентрации ионов Cr³⁺. Как видно из зависимостей на рис. 5.6, с увеличением содержания хрома

относительная интенсивность R-линий падает. Однако кинетика распада возбужденного состояния хрома при этом не меняется [19].

 

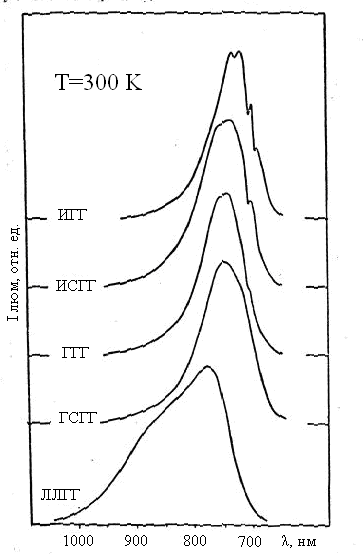
Рис. 4.4. Спектры люминесценции ионов хрома в кристаллах ИГГ, ИСГГ, ГГГ, ГСГГ и ЛЛГГ при Т=300 К

 

 

Рис. 4.5. Спектр люминесценции YAG:Cr³⁺ [7]

 

 

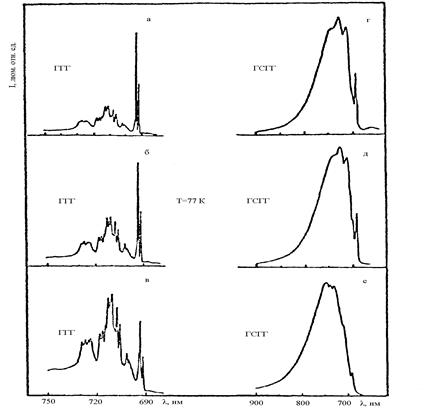
Рис. 4.6. Зависимость соотношения интенсивностей R-линий и широкой полосы люминесценции от концентрации ионов хрома в кристаллах ГГГ /содержание хрома 2·10¹⁹, 2,4·10²⁰, 8·10²⁰ см ^-3 – а, б, в/ и кристаллах ГСГГ /содержание хрома 6·10¹⁸, 6·10¹⁹, 3·10²⁰ см^-3 –г, д, е/ при Т=77К

 

Обращает на себя внимание изучение возможностей метода стереоатомного анализа для прогнозирования люминесцентных свойств ионов хрома в кристаллах. C целью построения модели и выявления зависимости ширины энергетического зазора ΔЕ₁₃ от структурных особенностей окружения положения, замещаемого хромом, методами стереоатомного анализа изучим некоторые соединения со структурой граната: Gd₃Ga₅O₁₂, Y₃Ga₅O₁₂, (Y_2.96Sc_0.04)(Sc_1.41Ga_0.59)Ga₃O₁₂, La_2.55Lu_2.45Ga_2.96O_11.93, Gd₃Sc₂Ga₃O₁₂, Y₃Al₂(AlO₄)₃, Y₃Sc₂Al₃O₁₂, Gd₃Sc₂Ga₃O₁₂, Y₃Ga₂Al₃O₁₂, Sr₃Y₂(GeO4)₃, Mg₃Y₂Ge₃O₁₂.

Структура соединений Gd₃Ga₅O₁₂, Y₃Ga₅O₁₂, (Y_2.96Sc_0.04)(Sc_1.41Ga_0.59)Ga₃O₁₂, La_2.55Lu_2.45Ga_2.96O_11.93, Gd₃Sc₂Ga₃O₁₂, изучена авторами работ [194-198]. Как и все гранаты, они относятся к кубической сингонии с пространственной группе Ia 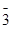d, параметр элементарной ячейки a принимает значения 12.3770 Ǻ, 12.2730 Ǻ, 12.4250 Ǻ, 12.9810 Ǻ, 12.5440 Ǻ соответственно. Например, в элементарной ячейке содержится 8 формульных единиц Gd₃Ga₅O₁₂, положение каждого из трех положительных ионов связано с различными координационными многогранниками. Ион Gd³⁺ окружен восемью ионами кислорода, образующими двенадцатигранник – деформированный куб. Ион Ga³⁺ (C_3i) окружен кислородным октаэдром, а ион Ga³⁺ (S₄) -тетраэдром. Позицию A₃ занимает Gd1, позицию B^I₂ – Ga1, позицию B^II₃ – Ga2. Данные рентгеноструктурного анализа, в частности для Gd₃Ga₅O₁₂, приведены в таблице 4.1.

 

 

Таблица 4.1. Данные рентгеноструктурного анализа для Gd₃Ga₅O₁₂

 

Name	No	DegOx	Wyckoff	X	Y	Z	S	CN
Ga			C3i	0.00000	0.00000	0.00000	1.000
Ga			S4	0.37500	0.00000	0.25000	1.000
Gd			D2	0.12500	0.00000	0.25000	1.000
O		-2	C1	0.02840	0.05490	0.64970	1.000

 

Как было замечено выше, при активировании граната ионами хрома, ион Cr³⁺ располагается в позиции В^I₂, в рассматриваемом гранате данную позицию занимает атом Ga1. Рассчитаем стереоатомные характеристики окружения этого атома и атомов, замещаемых хромом в других соединений с помощью программы Dirichlet комплекса Topos, используя структурные данные работ [20-24]. Результаты расчетов для Gd₃Ga₅O₁₂, Y₃Ga₅O₁₂, (Y_2.96Sc_0.04)(Sc_1.41Ga_0.59)Ga₃O₁₂, La_2.55Lu_2.45Ga_2.96O_11.93, Gd₃Sc₂Ga₃O₁₂ приведены в таблице 4.2.

 

 

Таблица 4.2. Стереоатомные характеристики соединений со структурой граната.

 

Соединение	X	SC	КЧ	VПВД, Å3	Rsd, Å	G3	Dist. Å
Gd3Ga5O12	Ga1	C3i		8.086	1.245	0.083876446	2.000
Y3Ga5O12	Ga1	C3i		7.868	1.234	0.084056683	1.980
(Y2.96Sc0.04)(Sc1.41Ga0.59)Ga3O12	Ga1	C3i		9.008	1.291	0.084154844	2.070
La2.55Lu2.45Ga2.96O11.93	Lu1	C3i		10.773	1.370	0.083791412	2.202
Gd3Sc2Ga3O12	Sc1	C3i		9.224	1.301	0.083968468	2.089

 

Порученные данные показывают, что для исследуемых соединений с увеличением расстояния (Dist.) B^I₂ – О синхронно увеличиваются радиус сферического домена и объем полиэдра Вороного-Дирихле, что объясняется кубической симметрией кристаллов со структурой граната.

Рассмотрев структурные особенности соединений Gd₃Ga₅O₁₂, (Y_2.96Sc_0.04)(Sc_1.41Ga_0.59)Ga₃O₁₂, Y₃Ga₅O₁₂, La_2.55Lu_2.45Ga_2.96O_11.93, Gd₃Sc₂Ga₃O₁₂, найдем связь между величиной энергетического зазора ∆Е₁₃ и объемом полиэдров Вороного-Дирихле (V_ПВД), сравнивая результаты измерений автора работы [25] с данными стереоатомного анализа (таблица 4.2). В таблице 4.3 приведены данные о величине энергетического зазора ∆Е₁₃ для иона Cr³⁺ в исследуемых матрицах и объеме полиэдров Вороного-Дирихле замещаемых атомов.

 

 

Таблица 4.3. Значения энергетического зазора и объема полиэдров ВД.

 

Гранат	∆Е13, см-1	VПВД, Å3
LLGG	-1000	10.773
GSGG (Sc2)		9.224
YSGG		9.008
GGG		8.086
YGG		7.868

 

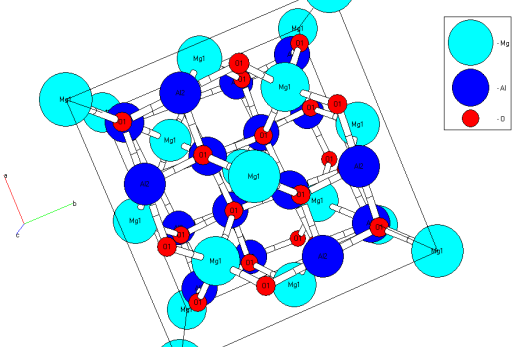
Рис. 4.7. Кристаллическая структура Mg Al₂O₄

 

 

 

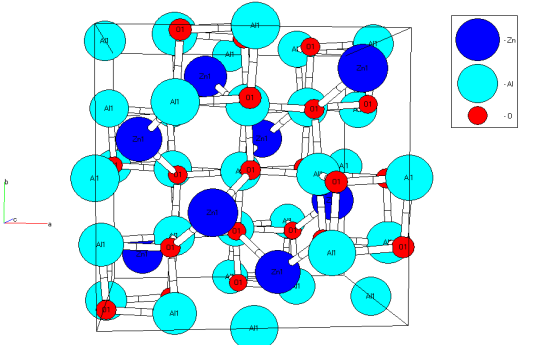
Рис. 4.8. Кристаллическая структура ZnAl₂O₄

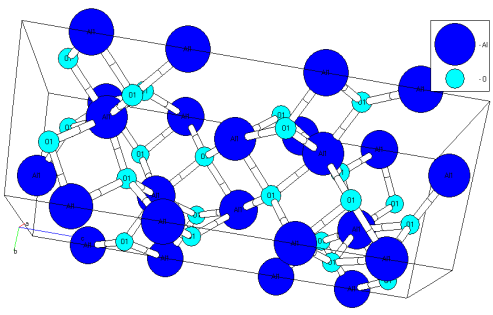
Рис. 4.9. Кристаллическая структура Al₂O₃

 

На рис. 4.10 показан график зависимости ∆Е₁₃ от V_ПВД, построенный по данным таблицы 4.3. Данные, которые приведены на рис. 4.10, с достаточной точностью аппроксимируются линией тренда у=-534.55х+4892.6 (см^-1), т.е. можно считать, что величина энергетического зазора ∆Е₁₃ для иона Cr³⁺ в исследуемых матрицах линейно зависит от объема полиэдров Вороного-Дирихле замещаемых атомов. Поэтому, зная значение V_ПВД замещаемого атома в любом соединения со структурой граната, можно прогнозировать величину энергетического зазора ∆Е₁₃ для иона Cr³⁺.

Оценим величину энергетического зазора ∆Е₁₃ иона Cr³⁺ для некоторых других кристаллов со структурой граната. По аналогии с предыдущими расчетами, используя данные рентгеноструктурного анализа

 

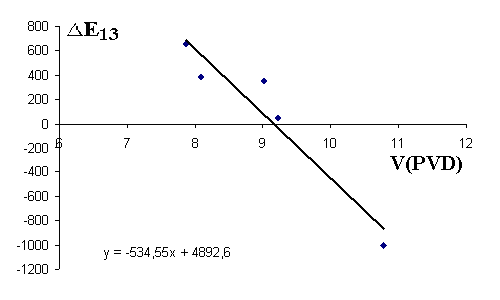
Рис. 4.10. График зависимости ∆Е₁₃ иона Cr³⁺ в соединениях со структурой граната от V_ПВД замещаемых атомов.

 

базы данных [26], вычислим V_ПВД для Y₃Al₂(AlO₄)₃, Y₃Sc₂Al₃O₁₂, Gd₃Sc₂Ga₃O₁₂, Y₃Ga₂Al₃O₁₂, Sr₃Y₂(GeO4)₃, и Mg₃Y₂Ge₃O₁₂. Значения V_ПВД приведены в таблице 5.4.

 

 

Таблица 4.4. Значения V_ПВД гранатов для элемента, находящегося в позиции В^I₂

 

	Соединение	Элемент	VПВД, Å3
1.	Y3Al2(AlO4)3	Al1	8.228
2.	Y3Sc2Al3O12	Sc1	8.973
3.	Gd3Sc2Ga3O12	Sc2	9.224
4.	Y3Ga2Al3O12	Ga2	9.446
5.	Sr3Y2(GeO4)3	Y1	11.382
6.	Mg3Y2Ge3O12	Y1	11.568

 

 

Используя значения V_ПВД, рассчитаем величину энергетического зазора ∆Е₁₃ для иона Cr³⁺ для вышеприведенных соединений со структурой граната. Подставляя в уравнение у=-534.55х+4892.6 значения х=V_ПВД, находим прогнозируемую величину энергетического зазора (таблица 5.5).

Данные, приведенные в таблице, показывают, что гранат Y₃Al₂(AlO₄)₃ с V_ПВД=8.228 ų имеет самое большое положительное значение энергетического зазора – 508.2 см^-1, а гранат Y₃Sc₂Al₃O₁₂ с V_ПВД= 8.973ų имеет самое маленькое положительное значение ∆Е₁₃=103.9 см^-1.

 

 

Таблица 4.5. Значения объема ПВД и прогнозируемого энергетического зазора ∆Е₁₃.

 

	Соединение	Элемент	VПВД, Å3	∆Е13, см-1
1.	Mg3Y2Ge3O12	Y1	11.568	-1304,3
2.	Sr3Y2(GeO4)3	Y1	11.382	-1203,4
3.	Y3Ga2Al3O12	Ga2	9.446	-152,7
4.	Gd3Sc2Ga3O12	Sc2	9.224	-32,2
5.	Y3Sc2Al3O12	Sc1	8.973	103,9
6.	Y3Al2(AlO4)3	Al1	8.228	508,2
7.	Al2O3	Al	7.177	1056.1
8.	Mg Al2O4	Mg	7.246	1019.2
9.	ZnAl2O4	Zn	7.158	1066.3

 

 

С помощью прикладных программ программного комплекса TOPOS установлено что структура карунда (Al₂O₃) принадлежит к пространственной решетке 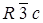, параметры ячейки у которой 4.7540. Структура шпинели (Mg Al₂O₄) принадлежит к пространственной решетке F 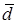m, параметр ячейки у которой 8.0830. Структура шпинели (ZnAl₂O₄) принадлежит к пространственной решетке F d 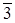m, параметры ячейки которой 8.0860.

 

Итак, с помощью прикладных программ Dirichlet программного комплекса TOPOS рассчитаны основные характеристики соединений со структурой граната. Выявлена зависимость ширины энергетического зазора ∆Е₁₃ от объема V_ПВД. Установлено, что зависимость можно аппроксимировать линейной функцией у=-534.55х+4892.6. С помощью установленной зависимости надежно прогнозируется ширина энергетического зазора ∆Е₁₃ гранатов: Y₃Al₂(AlO₄)₃, Y₃Sc₂Al₃O₁₂, Gd₃Sc₂Ga₃O₁₂, Y₃Ga₂Al₃O₁₂, Sr₃Y₂(GeO₄)₃, Mg₃Y₂Ge₃O₁₂.

 

Список использованных источников:

1. Grimes N, Kay H, Thompson P

Magnesium dialuminium oxide / Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences (76,1906-), стр. 333-345

2. Fischer P

Zinc dialuminium oxide MINR Gahnite - synthetic MINR Spinel group /Zeitschrift fuer Kristallographie,Kristallgeometrie, Kristallphysik, Kristallchemie (-144,1977), стр. 275-302

3. Ishizawa N, Marumo F, Minato I

Aluminium oxide - alpha MINR Corundum /Acta Crystallographica B (24,1968-38,1982), стр. 228-230

4. Каминский А.А., Аминов Л.К., Ермолаев В.Л. и др. Физика и спектроскопия лазерных кристаллов. М. Наука. 1986. 272 с.

5. Справочник по лазерам. Ред. Прохоров А.М. М. 1978. Сов. Радио. Т.1.

6. Geller S. Crystal chemistry of the garnets. //Z. Kristallographic. 1067. V. 125. № 1-6. P. 1-47.

7. O’Donnell K.P., Marshall A., Yamaga M. Vibronic structure in the photoluminescence spectrum of Cr³⁺ ions in garnets. //J. of Luminescence. 1989 V. 42 P. 365-373.

8. Ковба Л.М., Арсеньев П.А. Соединения редкоземельных элементов. Системы с оксидами элементов I- III групп. Серия «Химия редких элементов».М.: Наука, 1983. С. 280.

9. Кузьмичёва Г.М., Мухин Б.В., Жариков Е.В. Кристаллохимический анализ структурных особенностей гранатов. //Перспективные материалы. 1997. № 3. с.41-53.

10. Беляев Л.М., Любутин И.С., Милль Б.В. Катионное распределение в системе гранатов Ca₃In₂Sn_xGe_3-xO₁₂ по данным γ-резонансной спектроскопии. //Кристаллография, 1970. Т. 15. № 1. С. 174-175.

11. Недилько О.А. Изоморфное замещение в иттриево-алюминиевом гранате. //Украинский химический журнал. 1985. Т. 51. № 9. С. 899-901.

12. Морозова Л.Г., Феофилов П.П. Люминесцентное и рентгеноструктурное исследование системы 3Y₂O₃–(5-x)Ga₂O₃–xSc₂O₃. Изв. АН СССР. //Неорганические материалы. 1968. Т. 4. № 10. С. 1738-1743.

13. Кузьмичёва Г.М., Козликин С.Н. Кристаллохимический анализ образования твёрдых растворов на основе соединений со структурой граната. //Журнал неорганической химии. 1989. Т. 34. № 3. С. 576- 580.

14. Ефремов В.А., Захаров Н.Д., Кузьмичёва Г.М., Мухин Б.В. Иттрий- скандий- галлиевый гранат – кристаллическая структура. //Журнал неорганической химии, 1993. Т. 38. № 2. С. 220-225.

15. Ефиценко П.Ю., Касперович B.C., Кулешов А.А., Чарная Е.В. Исследование порядка в твёрдых растворах Y_xLu_3-xA1₅O₁₂ методами ЯМР. //Физика твёрдого тела, 1989. Т. 31. № 9. С. 170-173.

16. Stroka B., Hoist P., Tolksdorf W. An empirical formula for the calculation of lattice constants of oxide garnets based on substituted yttrium and gadolinium iron garnets. //Phillips J. Res., 1978. V. 33. № 3. -P. I86-202.

17. Зиновьев С.Ю., Кузьмичёва Г.М., Козликин С.Н. Особенности поведения твёрдых растворов редкоземельных галлиевых гранатов, содержащих скандий. //Журнал неорганической химии, 1990. Т. 35. № 9. С. 2197-2204

18. Аванесов А.Г., Данилов А.А., Денисов А.Л., Жариков Е.В. и др. Кристаллы иттрий-скандий-алюминиевого граната с хромом и неодимом как материал для активных сред твердотельных лазеров. //ДАН СССР. 1987. Т. 295. № 5. с. 1098-1191.

19. Аванесов А.Г., Балашов А.Б., Жуйко И.П., Игнатьев Б.В. и др. Особенности деактивации возбужденных состояний иона Cr³⁺ в кристаллах. Квантовая электроника. 1989. Т. 16. № 10. с. 2083-2086.

20. Sawada H. Electron density study of garnets: Z₃Ga₅O₁₂; Z = Nd, Sm, Gd, Tb. //Journal of Solid State Chemistry. 1997. V. 132. P. 300-307.

21. Nakatsuka A., Yoshiasa A., Takeno S. Site preference of cations and structural variation in Y₃Fe_5-xGa_xO₁₂ (0<x<5) solid solutions with garnet structure. Acta Crystallographica B. 1995. V. 51. P. 737-745.

22. Efremov V.A., Zakharov N.D., Kuz'micheva G.M., Mukhin B.V., Chernyshev V.V. Yttrium-scandium-gallium garnet:the crystal structure. //Zhurnal Neorganicheskoi Khimii. 1993. V. 38. P. 220-225.

23. Yamazaki S., Marumo F., Tanaka K., Morikawa H., Kodama N., Kitamura K., Miyazawa Y. A structural study of facet and off-facet parts of rare-earth garnets, Gd₃Sc₂Al₃O₁₂, Gd₃Sc₂Ga₃O₁₂, and La₃Lu₂Ga₃O₁₂ La_2.55Lu_2.45Ga_2.96O_11.93. //Journal of Solid State Chemistry.1994. V. 108. P. 94-98.

24. Kondratyuk I.P., Zharikov E.V., Simonov V.I. Refinement of atomic structures of Gd₃Sc₂Ga₃O₁₂ and (Gd_0.8Nd_0.2)Sc₂Ga₃O₁₂. //Kristallografiya. 1988. V. 33. P. 51-56.

25. Grinberg M. ²E→⁴A₂ fluorescence of Cr³⁺ in high and intermediate field garnets. //J. of Luminescence. 1993. T. 54. P. 369-382.

26. Inorganic crystal structure database. Gmelin-Institut fur Anorganische Chemie & FIC Karlsruhe. 2004.