Экономико-статистическое моделирование

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

вариант №7

по предмету «МЕТОДЫПРОГНОЗИРОВАНИЯ И ПЛАНИРОВАНИЯ»

 

 

Выполнил студент гр. 015-142 В. Г. Фёдоров

 

 

Преподаватель А. В. Стрикунов

 

Псков

2010 год

СОДЕРЖАНИЕ

Стр.

 

1 Метод экспертных оценок в задачах многокритериальной оптимизации.....3

 

2 Методы экспертных оценок в задачах теории нечётких множеств………….4

 

3 Методы экстраполяции (аппроксимация динамического ряда аналитическими функциями)………………………………………………………………..5

 

4 Экономико-статистическое моделирование…………………………………..8

 

5 Оптимизационные модели…………………………………………………….12

 

6 Нормативный метод планирования…………………………………………..14

 

7 Балансовый метод планирования……………………………………………..16

 

8 Графический метод планирования…………………………………………...17

 

9 Прогнозирование численности населения…………………………………...20
1 Методы экспертных оценок в задачах многокритериальной

Оптимизации

Задача 1

В качестве показателей, характеризующих студенческие научные работы, были выбраны следующие:

- оценка за презентацию работы;

- оценка научной новизны;

- оценка за логичность и обоснованность положений, изложенных в работе.

Экспертная оценка значимости показателей по 10-ти балльной шкале представлена в таблице 1.

Таблица 1

Результаты экспертной оценки

Эксперт	Показатель
Презентация работы	Научная новизна	Логичность и обоснованность работы

 

Оценка показателей, характеризующих научные работы студентов по 10-ти балльной шкале, представлены в таблице 2.

Таблица 2

Значения показателей, характеризующих научные работы студентов

Автор работы	Значение показателей
Презентация работы	Научная новизна	Логичность и обоснованность работы
Иванова С.И.
Леонидов П.А.
Сергеев А.П.

 

Определите автора лучшей студенческой научной работы.

Решение:

1) Определим значение весовых коэффициентов, т.е.

; ; , тогда

.

2) Приведём показатели к единому безразмерному масштабу

.

3) Решим матрицу в виде системы уравнений

Ответ: максимальное значение целевой функции соответствует второй программе. Следовательно, автором лучшей работы является Леонидов П. А.

Методы экспертных оценок в задачах теории нечетких множеств

Задача 2

Согласно экспертной оценке, в зависимости от степени загрязнения воды большой фильтр очистит Б=(80;100;10;15;0,9) м.куб. воды, а фильтр малого размера М=(40;40;5;5;0,8) м.куб. Сколько воды очистят 8 больших фильтров и 12 фильтров малого размера.

Решение:

Имеются два нечётких числа:

Б=(80;100;10;15;0,9)

М=(40;40;5;5;0,8)

Необходимо подсчитать, сколь воды очистят 8 больших фильтров и 12 фильтров малого размера, для этого

8Б=(640;800;80;120;7,2)

12М=(480;480;60;60;9,6)

 

, тогда

;

;

;

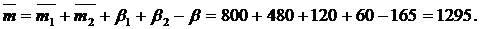
Таким образом, 8Б+12М=(1105;1295;125;165;7,2).

Функция принадлежности числа 8Б+12М представлена на рисунке 1.

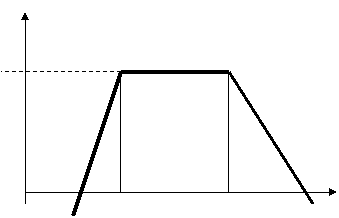
980 1105 1295 1460

Рис. 1 Функция принадлежности прогнозного значения очистки загрязнённой воды малым и большим фильтрами

 

Методы экстраполяции (аппроксимация динамического ряда аналитическими функциями)

Задача 3

В таблице 3 приведены данные об экспорте черных металлов и меди. Используя линейную функцию, составьте прогноз экспорта черных металлов и меди на ближайшую перспективу.

Таблица 3

Экспорт черных металлов и меди из РФ

Продукция	Год
Черные металлы, млн. долл. США
Медь, тыс. тонн

Сделайте выводы.

Решение:

1) Результаты предварительных расчётов по экспорту чёрных металлов и меди из Российской Федерации (Таблица 4, 5):

Таблица 4

Результаты предварительных расчётов эмпирических коэффициентов по экспорту чёрных металлов, млн. долл. США

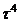
Год					Чёрные металлы
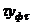
Сумма

 

Таблица 5

Результаты предварительных расчётов эмпирических коэффициентов по экспорту меди, тонн

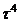
Год					Медь
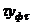
Сумма

 

2) Решим систему уравнений для определения параметров линейной функции, т.е.

Для чёрных металлов: , тогда имеем:

Для меди: 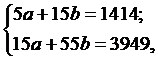, тогда имеем:

Следовательно, линейная функция будет иметь следующий вид:

- для чёрных металлов: ;

- для меди: .

Соответственно, прогноз экспорта на 2009 год будет:

- для чёрных металлов: млн. долл. США;

- для меди: тонн.

3) Предварительные расчёты среднеквадратического отклонения от линейного тренда (Таблица 6, 7):

Таблица 6

Предварительные расчёты среднеквадратического отклонения от линейного тренда по экспорту чёрных металлов, млн. долл. США

Год	Экспорт чёрных металлов, млн. долл. США	Вид уравнения
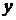
		18420,5
		24627,5
Сумма

 

Таблица 7

Предварительные расчёты среднеквадратического отклонения от линейного тренда по экспорту меди, тонн

Год	Экспорт меди, тонн	Вид уравнения
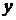
		341,4	1,96
		312,1	1,21
		282,8	139,24
		253,5	1056,25
		224,2	331,24
Сумма			1529,9

 

4) Найдём среднеквадратическое отклонение от линейного тренда:

- для чёрных металлов: ;

- для меди: .

Тогда ширина доверительного интервала (при ):

- для чёрных металлов: ;

- для меди: .

5) Интервальный прогноз:

- для чёрных металлов: или ;

- для меди: или .

Вывод: прогнозный расчёт экспорта чёрных металлов и меди на ближайшую перспективу показал, что:

- в 2009 году экспорт чёрных металлов продолжит возрастать умеренными темпами и достигнет показателя в 30834,5 млн. долл. США. В дальнейшем объём экспорта чёрных металлов будет колеблется в интервале млн. долл. США;

- в 2009 году экспорт меди продолжит умеренное снижение и достигнет показателя в 194,9 тонн. В дальнейшём объём экспорта меди будет колеблется в интервале тонн.

Экономико-статистическое моделирование

Задача 4

Известно, что на заболеваемость населения простудными заболеваниями влияют такие факторы как уровень доходов населения, возрастной состав населения, природно-климатические условия (температура воздуха). В таблице 8 приведены статистические данные о значениях данных факторов и заболеваемости населения. Построить экономико-статистическую модель зависимости заболеваемости населения от влияющих факторов.

Таблица 8

Значения показателей

 

Область	Среднедушевой доход, руб./мес.	Доля населения старше трудоспособного возраста, %	Средняя температура воздуха в январе,	Количество зарегистрированных заболеваний на тыс. человек
Псковская		25,2	-2,1
Новгородская		24,6	-3,6
Калининградская		20,9	3,3
Архангельская		19,9	-7,3
Мурманская		16,1	-8,9
Вологодская		21,4	-7,2

Сделайте выводы.

Решение:

При построении экономико-статистической модели будем исходить из предположения, что зависимость между результирующим фактором (количество зарегистрированных заболеваний - ) и влияющими факторами (среднедушевой доход - 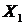, доля населения старшего трудоспособного возраста - 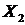, средняя температура воздуха в январе - ) имеет линейный вид:

Система уравнений, в результате решения которой будут определены эмпирические коэффициенты, будет следующей:

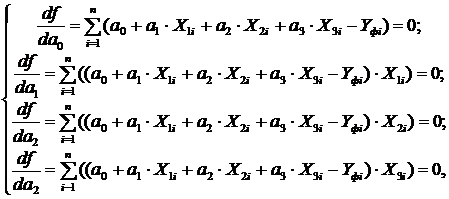
или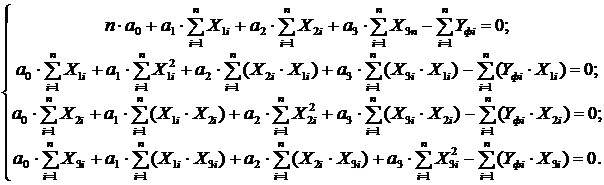

 

Промежуточные расчёты эмпирических коэффициентов сведём в таблице 9, 10.

Таблица 9

Промежуточные расчёты эмпирических коэффициентов

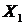
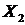
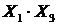
		25,2	-2,1		635,04	4,41	258022,8	-21501,9	-52,92
		24,6	-3,6		605,16	12,96		-41652	-88,56
		20,9	3,3		436,81	10,89			68,97
		19,9	-7,3		396,01	53,29	288052,5	-105667,5	-145,27
		16,1	-8,9		259,21	79,21	301166,6	-166483,4	-143,29
		21,4	-7,2		457,96	51,84	258447,8	-86954,4	-154,08
		128,1	-25,8		2790,19	212,6	1654696,7	-380514,2	-515,15

 

Таблица 10

Промежуточные расчёты эмпирических коэффициентов

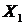
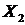
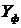
		25,2	-2,1				-1008
		24,6	-3,6				-1512
		20,9	3,3
		19,9	-7,3				-2555
		16,1	-8,9				-2225
		21,4	-7,2				-2880
		128,1	-25,8				-9190

После подстановки результатов промежуточных расчетов в систему уравнений, имеем:

 

Решим данную систему уравнений. Для этого представим данную систему в матричном виде, т.е.

Тогда вектор-столбец эмпирических коэффициентов равен:

 

 

Рассчитаем обратную матрицу (воспользовавшись программой Microsoft Excel):

 

Перемножим полученную обратную матрицу на вектор столбец (воспользовавшись программой Microsoft Excel). На основе рассчитанных значений составим экономико-статистическую модель зависимости количества регистрируемых заболеваний от исследуемых факторов, т.е.

Найдём теоретическое значение результативного показателя, к примеру, по Псковской области:

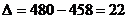
Результаты расчётов по экономико-статистической модели по регионам России представим в таблице 11.

Таблица 11

Результаты расчётов по экономико-статистической модели

Область	Теоретическое значение,	Фактическое значение,	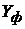Отклонение,
Псковская
Новгородская			-32
Калининградская			-1
Архангельская
Мурманская
Вологодская

 

Вывод: анализируя данные, представленные в таблице 11, следует отметить, что, с одной стороны отклонение теоретических значения результирующего фактора от фактических значений может носить случайный характер. С другой стороны вполне возможно, что в Новгородской и Калининградской областях факторы, оказывающие влияние на уровень зарегистрированных заболеваний подсчитаны недостаточно точно, или же существуют другие факторы, которые не были учтены изначально.

Оптимизационные модели

Задача 5

 

Выплавка сплава производится из трех видов сырья (таблица 12).

 

Таблица 12

Параметры сырья

Параметр	Руда
Содержание углерода, %	0,4	1,4
Содержание хрома, %	0,2
Содержание никеля, %
Содержание серы, %	0,08	0,05
Цена, руб./тонну

 

В сплав должно входить:

не менее 0,7% углерода;

не менее 15% хрома;

не менее 6% никеля;

не более 0,06% серы.

Определите процентное содержание сырья каждого вида.

Решение:

Обозначим виды сырья буквами А, В, С. Процентное содержание их в сплаве обозначим . Тогда уравнением сплава будет:

.

Учитывая уравнение сплава, а также имеющиеся в условии ограничения, составим систему неравенств, т.е.

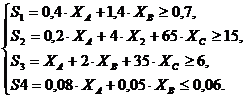
Преобразуем данную систему неравенств в систему уравнений и решим её:

Выразим: , подставим в одно из уравнений, получаем

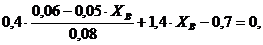
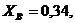тогда

Найдём , подставив найденные значения в одно из уравнений, т.е.

Учитывая процентное содержание каждого вида сырья в сплаве, представляется возможным рассчитать стоимость сплава, т.е.

Ответ: данное решение свидетельствует о том, что искомый сплав будет содержать: сырья А – 53%, сырья В – 34 %, сырья С – 13 %

 

6 Нормативный метод планирования

Задача 6

Из стального листа размером 20 3000 1250 мм нарезаются заготовки размером 20 800 600 мм. Плотность стали – 7,8 . Определите норму затрат материала на заготовку, если цена на стальной лист установлена в рублях за тонну.

Решение:

Чтобы определиться с возможным количеством вырезанных из данного листа заготовок, найдём необходимые объёмы, т.е.

Масса листа (заготовки) находится, как произведение плотности стали на объём: , тогда

Тогда без учёта потерь и геометрии разрезов максимальное количество заготовок будет ровняться: , т.е. 7 деталей. Но данное количество деталей возможно получить лишь при использовании лазера, ширина разреза которого рассчитывается в микронах. Поэтому рассмотрим и другие варианты.

Следует напомнить, что нам необходимо найти норму затрат, которая рассчитывается как отношение массы листа к количеству заготовок, которые возможно будет вырезать: .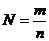

Исходя из этого, определим норму затрат при изготовлении 7 заготовок, т.е. .

Разместим заготовки так, как показано на рисунке 2.

Рис. 2 Распределение заготовок на стальном листе

Для данного случая: n=6, тогда норма затрат будет равняться: .

Если разместить детали по-другому (рис. 3):

Рис. 3 Распределение заготовок на стальном листе

Для данного случая n=4, тогда норма затрат будет равняться: .

Ответ: сравнивая рассчитанные нормы затрат, не трудно заметить, что наименьшее значение данный показатель приобретает при изготовлении из стального листа 7 заготовок. Но изготовление 7 деталей требует использование инновационных технологий – лазера. Поэтому наиболее вероятный вариант – это изготовление 6 заготовок. При этом норма затрат будет равняться 97,5 .

7 Балансовый метод планирования

Задача 7

Для производства 1 тонны стали в качестве ресурса необходимо 2 тонны угля, а для 1 тонны угля – 0,1 т стали. Плановое потребление угля -2000 тонн, а стали – 1000 тонн. Найдите валовой выпуск стали и угля.

Решение:

Найдём валовой выпуск стали и угля.

Плановое потребление угля на производстве – 2000 тонн. Для производства 1 тонны угля необходимо 0,1 тонны стали, тогда для производства 2000 тонн: тонн стали.

Плановое производство стали на производстве – 1000 тонн. Для производства 1 тонны стали необходимо 2 тонны стали, тогда для производства 1000 тонн: тонн угля.

Сведём полученные результаты в баланс и найдём валовой выпуск угля и стали (Таблица 13).

Таблица 13

Баланс валового выпуска угля и стали

Производство	Потребление, тонн	Плановое потребление, тонн	Валовой выпуск, тонн
Угль	Сталь
Угль	-
Сталь		-

Ответ: валовой выпуск угля 4000 тонн, валовой выпуск стали 1200 тонн.

8 Графический метод планирования

Задача 8

Перечень работ по реализации проекта по сооружению линии электропередачи приведен в таблице 13.

Таблица 13

Перечень работ по сооружению линии электропередачи

Работа	Продолжительность выполнения, мес.	№ предшествующей работы
1. Подготовка к работам	0,5	-
2. Трассировка ЛЭП
3. Проведение изысканий по трассе ЛЭП
4. Технико-экономическое обоснование сооружения ЛЭП
5. Проектирование ЛЭП
6. Оформление заказа на строительно-монтажные материалы		4, 5
7. Оформление заказа на опоры		4, 5
8. Оформление заказа на провода, изоляторы, грозозащитный трос		4, 5
9. Получение строительно-монтажных материалов
10. Получение опор
11. Установка опор	1,5
12. Получение проводов, троса, изоляторов
13. Подвеска проводов, грозозащитного троса	2,5	11, 12
14. Маркировка и проведение испытаний

 

Постройте сетевой и линейный графики реализации проекта сооружения линии электропередачи. Определите сроки реализации проекта.

Решение:

Для построения сетевого графика определим перечень работ:

0 – начало работы;

1 – подготовка к работам;

2 - трассировка ЛЭП;

3 – проведение изысканий по трассе ЛЭП;

4 – технико-экономическое обоснование сооружения ЛЭП;

5 – проектирование ЛЭП;

6 – оформление заказа на строительно-монтажные материалы;

7 – оформление заказа на опоры;

8- оформление заказа на провода, изоляторы, грозозащитный трос;

9 – получение строительно-монтажных материалов;

10 – получение опор;

11 – установка опор;

12 – получение проводов, троса, изоляторов;

13 – подвеска проводов, грозозащитного троса;

14 – маркировка и проведение испытаний.

На основе перечня событий и работ построим сетевой график (рис. 4).

Рис. 4 Сетевой график проекта по сооружению линии электропередач

На основании сетевого графика, работы в ходе сооружения линии электропередач будут иметь следующую кодировку:

0-1 – подготовка к работам;

1-2 – трассировка ЛЭП;

2-3 – проведение изысканий по трассе ЛЭП;

3-4 – технико-экономическое обоснование сооружения ЛЭП;

3-5 – проектирование ЛЭП;

4-6 – оформление заказа на строительно-монтажные материалы;

4-7 - оформление заказа на опоры;

4-8 – оформление заказа на провода, изоляторы, грозозащитный трос;

6-9 – получение строительно-монтажных материалов;

7-10 – получение опор;

10-11 – установка опор;

8-12 – получение проводов, троса, изоляторов;

12-13 – подвеска проводов, грозозащитного троса;

13-14 – маркировка и проведение испытаний.

Начертим выполнение работ на линейном графике (рис. 5)

Рис. 5 Линейный график реализации проекта сооружения линии электропередач

Ответ: максимальная продолжительность выполнения работ по реализации проекта сооружения линии электропередач составляет 17,5 месяца.