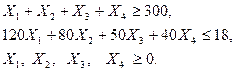ФГОУ ВПО Бурятская государственная сельскохозяйственная академия
Имени В.Р. Филиппова
Кафедра информатики и информационных технологий в экономике
Е.О. Ванзатова
Методические указания и задания для самостоятельной работы студентов экономического факультета
Очной формы обучения специальности 010502
«Прикладная информатика в экономике АПК»
По дисциплине «Математическая экономика»
Улан-Удэ
Изд-во БГСХА
2007 г.
Решение задач линейного программирования
С помощью поиска решений в среде Excel.
Общая задача оптимизации.
Примеры задач линейного программирования.
В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Рассмотрим несколько примеров задач линейного программирования (ЗЛП).
Задача оптимального использования ресурсов
Фабрика имеет в своём распоряжении определённое количество ресурсов: рабочую силу, деньги, сырьё, оборудование, производственные площади и т.п. Допустим, например, ресурсы трёх видов: рабочая сила, сырьё и оборудование – имеются в количестве соответственно 80 (чел/дней), 480 (кг) и 130 (станко/ч). Фабрика может выпускать ковры четырёх видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице.
| Ресурсы | Нормы расхода ресурсов на единицу изделия | Наличие ресурсов | |||
| ковёр «Лужайка» | ковёр «Силуэт» | ковёр «Детский» | ковёр «Дымка» | ||
| Труд | |||||
| Сырьё | |||||
| Оборудование | |||||
| Цена (тыс. руб.) |
Требуется найти такой план выпуска продукции, при котором будет максимальная общая стоимость продукции.
Обозначим через Х1, Х2, Х3, Х4 количество ковров каждого типа.
Экономико-математическая модель задачи.
Целевая функция – это выражение, которое необходимо максимизировать:
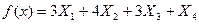
Ограничения по ресурсам
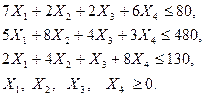
Задача о размещении производственных заказов.
Необходимо в планируемом периоде обеспечить производство 300 тыс. однородных новых изделий, которые могут выпускаться на четырёх филиалах предприятия. Для освоения этого нового вида изделий нужны определённые капительные вложения. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами удельных капитальных вложений и себестоимостью единицы продукции в соответствии с таблицей.
| Показатель | Филиал предприятия | |||
| Себестоимость производства изделия, руб. | ||||
| Удельные капиталовложения, руб. |
Себестоимость производства и удельные капиталовложения для каждого из филиалов условно приняты постоянными, т.е. потребность в капитальных вложениях и общие издержки будут изменяться пропорционально изменению объёмов производства изделий.
Предположим, что на все филиалы предприятие для освоения 300 тыс. новых изделий может выделить 18 млн. руб. Необходимо найти такой вариант распределения объёмов производства продукции и капитальных вложений по филиалам, при котором суммарная стоимость изделий будет минимальной.
Модель задачи.
Введём следующие обозначения:
i – номер филиала (i = 1,…, n; n = 4);
Xi – объём выпускаемой продукции на i -ом филиале предприятия;
Т – суммарная потребность в изделиях (Т = 300 тыс. шт);
К – выделяемые капиталовложения (К = 18 млн. руб.);
Сi – себестоимость производства продукции на i -ом филиале предприятия;
ki – удельные капиталовложения на единицу продукции на i -ом филиале.
Экономико-математическая модель задачи в символах будет иметь вид:
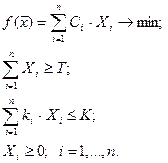
С учётом имеющихся данных модель задачи имеет вид:
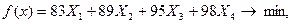
ограничения