Excel позволяет представить результаты поиска решения в форме отчёта. Существует три типа таких отчётов:
Результаты (Answer). В отчёт включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
Устойчивость (Sensitivity). Отчёт, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчёт включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

В отчёте по результатам содержатся оптимальные значения переменных X1, X2, X3, X4, которые соответственно равны 0, 30, 10, 0, значение целевой функции – 150, а также левые части ограничений.
Транспортная задача
Транспортная задача является одной из наиболее распространённых задач линейного программирования и находит широкое практическое приложение.
Постановка транспортной задачи. Некоторый однородный продукт, сосредоточенный у k поставщиков Аi в количестве аi (i = 1,…,k) единиц, необходимо доставить n потребителям Bj в количестве bj (j=1, …, n) ед. Известна стоимость сij перевозки единицы груза от i -го поставщика к j -му потребителю.
Необходимо составить план перевозок, позволяющий вывести все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость.
Сформулируем экономико-математическую модель транспортной задачи. Обозначим через xij количество единиц груза, запланированных к перевозке от i -го поставщика к j -му потребителю. Так как от i -го поставщика к j -му потребителю запланировано к перевозке xij единиц груза, то стоимость перевозки составит сij xij.
Стоимость всего плана выразится двойной суммой

Систему ограничений получаем из следующих условий задачи:
а) все грузы должны быть перевезены, т.е.
 ,
,
б) все потребности должны быть удовлетворены, т.е.
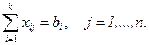
Таким образом, математическая модель транспортной задачи имеет следующий вид: найти минимальное значение линейной функции

при ограничениях

 (*)
(*)
В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е.

Транспортная задача, в которой суммарные запасы и потребности совпадают, т.е. выполняется условие (2.4.5), называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая:
а) суммарные запасы превышают суммарные потребности
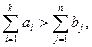
б) суммарные потребности превышают суммарные запасы

Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.
Найти минимальное значение линейной функции

при ограничениях
 (случай а)
(случай а)
 (случай б)
(случай б)
Открытая модель решается приведением к закрытой модели.
В случай а, когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель Bn+1, потребность которого

В случае б, когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик Ak+1, запасы которого

Как стоимость перевозки единицы груза до фиктивного потребителя, так и стоимость перевозки груза от фиктивного поставщика полагаются равными нулю, так кА груз в обоих случаях не перевозится.
Транспортная задача имеет n+k уравнений с k∙n неизвестными.
Матрицу Х=(xij)k,n, удовлетворяющую условиям (*) называют планом перевозок транспортной задачи (xij – перевозками).
План Х*, при котором целевая функция обращается в минимум, называется оптимальным.