Кафедра «Электрические машины и общая электротехника»
Расчет трехфазной линейной электрической цепи
Практическая работа
по дисциплине «Электротехника и электроника»
ИНМВ. 70048. 000 ПЗ
Студент гр.30Е
А. А. Пырма
Руководитель –
к.т.н., доцент каф. ЭМ и ОЭ
Ю. В. Москалев
Омск 2012
Задание
студенту гр.30Е Пырма А. А.
на практическую работу по теме:
«Расчет трехфазной линейной электрической цепи»
Для трехфазной линейной электрической цепи, необходимо следующее:
1 При соединении приемников «звездой» определить значения тока в линейных и нейтральном проводах, построить векторные диаграммы напряжений и токов при работе цепи в следующих режимах: а) при симметричной системе напряжений; б) обрыве одной фазы; в) обрыве нейтрального провода и коротком замыкании одной фазы.
2 Определить значения потребляемой активной и реактивной мощности трехфазной цепи в режиме пункт 1, а.
3 При соединении «треугольником» определить фазные и линейные токи, значения потребляемой активной и реактивной мощности. Построить векторные диаграммы напряжений и токов.
Исходные данные в практической работе приняты по варианту 48. Расчетная схема приведена на рисунке 1, значения параметров элементов цепи приведены в таблице 1.

Рисунок 1 – Расчетная схема
Таблица 1 – Числовые значения параметров элементов схемы
| Вариант | Напряжение, В | Сопротивление, Ом | Обрыв фазы | К.з. фазы | |||
| XL1 | ХL2 | R3 | ХС3 | ||||
| B | C |
Содержание
Введение………………………………………………………………………………..….4
1 Соединение приемников «звездой»………………………………………………….5
2 Неравномерная нагрузка при обрыве линейного провода …………………………7
3 Обрыв нейтрального провода при коротком замыкании фазы ……………………8
4 Соединение приемников «треугольником»…………………………………………10
Заключение……………………………………………………………………………....13
Библиографический список……………………………………………………………14
Введение
В данной работе будут определены значения тока в линейных и нейтральном проводах символическим методом при соединении нагрузок в «звезду» и «треугольник», а также при обрыве линейного провода и коротком замыкании, построены векторные диаграммы напряжений и токов. Также будут рассчитаны значения потребляемой активной и реактивной мощности трехфазной цепи.
1 Соединение приемников «звездой»
Наличие нейтрального провода оставляет систему напряжений симметричной даже при неравномерной нагрузке. Если пренебречь сопротивлением линейных и нейтрального проводов, то можно считать, что фазное
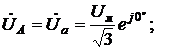 (1)
(1)
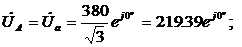
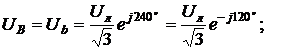 (2)
(2)
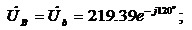
 (3)
(3)
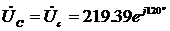
и линейное
 ; ;
| (4) |  ; ;
|
 ; ;
| (5) |  ; ;
|
 ; ;
| (6) | 
|
напряжение приемника и источника имеет одинаковые значения во всех фазах соответственно. Смещение нейтрали нагрузки отсутствует.
Значения сопротивления нагрузок фаз рассчитываются по формулам:
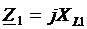 ; ;
| (7) | 
|
 ; ;
| (8) |  ; ;
|
 ; ;
| (9) | 
|
Фазный и линейный ток при соединении нагрузки «звездой» есть одно и то же. Значения тока определяем по закону Ома:
 ; ;
| (10) |  А; А;
|
 ; ;
| (11) | 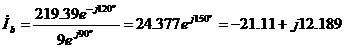 А; А;
|
 ; ;
| (12) |  А. А.
|
В соответствии с первым законом Кирхгофа ток в нейтральном проводе при неравномерной нагрузке будет равен сумме токов фаз:
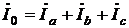 ; (13)
; (13)

Мощность, потребляемая цепью при соединении «звездой», может быть найдена как сумма мощностей трех фаз:
активная –
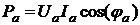 ; ;
| (14) |  ; ;
|
 ; ;
| (15) |  ; ;
|
 ; ;
| (16) | 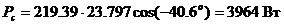 ; ;
|
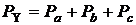 ; ;
| (17) |  ; ;
|
реактивная –
 ; ;
| (18) | 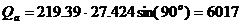 вар; вар;
|
 ; ;
| (19) | 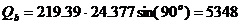 вар; вар;
|
 ; ;
| (20) |  вар; вар;
|
 ; ;
| (21) | 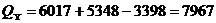 вар; вар;
|
полная мощность –
 ; ;
| (22) | 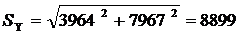 В∙А; В∙А;
|

Рисунок 1.1 – Векторная диаграмма напряжений и токов при соединении «звездой»
|
Схема цепи при обрыве линейного провода фазы В представлена на рисунке 2.1.Напряжение на нагрузке оборванной фазы  . Напряжение других фаз остается неизменным. Значения тока в фазах А и С тоже не изменились.
. Напряжение других фаз остается неизменным. Значения тока в фазах А и С тоже не изменились.
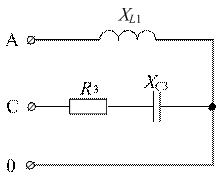
Рисунок 2.1 – Обрыв линейной фазы В
Ток в нейтральном проводе рассчитывается по формуле:
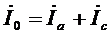 ; (23)
; (23) 

Рисунок 2.2 - Векторная диаграмма напряжений и токов для неравномерной нагрузки при обрыве линейного провода фазы В
3 Обрыв нейтрального провода при коротком замыкании фазы
Обрыв нейтрального провода при коротком замыкании фазы С сопровождается смещением нейтрали приемника на величину фазного напряжения. Нейтральная точка приемника 0' совпадает при к. з. фазы С с вершиной С треугольника линейных напряжений, потому что  , так как нагрузка фазы С при к. з. равна нулю:
, так как нагрузка фазы С при к. з. равна нулю: 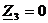 .
.

Рисунок 3.1 – Обрыв линейного провода и короткое замыкание фазы С
Напряжение двух других фаз по величине возрастает до значения линейного напряжения, В:
 (24)
(24) 
 (25)
(25) 
Токи фаз А и В можно рассчитать:
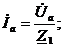 (26)
(26) 
 (27)
(27) 
Ток в короткозамкнутой фазе в соответствии с первым законом Кирхгофа определяется по выражению:
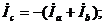 (28)
(28)
 А.
А.

Рисунок 3.2 - Векторная диаграмма напряжений и токов при обрыве нейтрального провода и коротком замыкании фазы С
4 Соединение приемников «треугольником»
Схема соединения приведена на рисунке 4.1. В качестве приемников использованы те же сопротивления. В соответствии со способом соединения приемники включены между линейными проводами и в индексах обозначений ставятся две буквы.

Рисунок 4.1 – Схема соединения «треугольником»
При соединении «треугольником» линейное напряжение является одновременно и фазным как для источника, так и для приемника, если пренебречь сопротивлением соединительных проводов:
 В;
В;  В; (29)
В; (29)
 В. (30)
В. (30)
Значения тока в фазах определяются по закону Ома:
 ; ;
| (31) |  А; А;
|
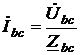 ; ;
| (32) |  А; А;
|
 ; ;
| (33) | 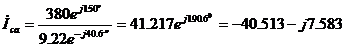 А. А.
|
Линейные токи находят по первому закону Кирхгофа для узлов а, в, с:
 (34)
(34)
 А;
А;
 (35)
(35)
 А;
А;
 ; (36)
; (36)
 А.
А.
Значения мощности, потребляемой в цепи при соединении «треугольником», определяются по выражениям:
активная –
 ; ;
| (37) |  ; ;
|
 ; ;
| (38) |  ; ;
|
 ; ;
| (39) |  ; ;
|
 ; ;
| (40) |  ; ;
|
реактивная –
 ; ;
| (41) | 
|
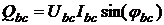 ; ;
| (42) |  ; ;
|
 ; ;
| (43) |  вар; вар;
|
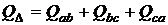 ; ;
| (44) |  вар; вар;
|
полная –
 ; ;
| (45) |  ; ;
|

Рисунок 4.2 – Векторная диаграмма напряжений и токов при соединении нагрузки «треугольником»
Заключение
Расчет однофазной цепи переменного тока символическим методом выполнен верно, так как векторная диаграмма сходится. Кроме того полная мощность при соединении в «треугольник» в 3 раза больше, чем при соединении в «звезду»: 
 Библиографический список
Библиографический список
1. С е р к о в а Л. Е. Анализ режимов работы электрических и магнитных цепей: Учебное пособие / Л. Е. С е р к о в а, В. В. Х а р л а м о в, П. К. Ш к о д у н.
ОмГУПС. Омск, 2005. 83 с.
2. Электротехника / Под ред. В. Г. Г е р а с и м о в а. – М.: Высшая школа, 1985. 480 с.
3. К а с а т к и н А. С., Н е м ц о в Н. В. Электротехника. – М.: Высшая школа, 2000.