Суть решения физических задач методом Монте-Карло заключается в том, что физическому явлению сопоставляется имитирующий вероятностный процесс, отражающий его динамику (другими словами каждому элементарному акту процесса сопоставляется некоторая вероятность его осуществления). Затем этот процесс реализуется с помощью набора случайных чисел. Интересующие нас значения физических величин находятся усреднением по множеству реализаций моделируемого процесса.
Основным преимуществом метода Монте-Карло по сравнению с классическими численными методами состоит в том, что с его помощью можно исследовать физические явления практически любой сложности, которые иначе решить просто невозможно. Например, решить уравнения, описывающие взаимодействие двух атомов, будет сравнительно несложно, однако решить такую же задачу для сотни атомов уже не реально. Кроме того, для метода Монте-Карло часто характерна простая структура вычислительного алгоритма. Как правило, составляется программа для осуществления одного случайного испытания (шага модели). Затем это испытание повторяется необходимое число раз, причем каждый последующий шаг не зависит от всех остальных.
Метод Монте-Карло можно также назвать "теоретическим экспериментом". Действительно, если точно известны законы элементарных актов, а вместе с ними и вероятности элементарных событий, результаты, получаемые этим методом, были бы подобны экспериментальным данным.
Моделирование хаотического движения частиц
В качестве примера использования метода Монте-Карло в моделировании физических явлений построим модель одномерного диффузионного процесса.
Выполним расчет для статистического ансамбля из N частиц, которые начинают движение из начала координат.
Программа в MathCAD
| Количество процессов (или количество диффундирующих частиц)
|
| Количество шагов смещения в процессе диффузии
|
| Шаги смещения, заданные как значения случайной величины с равномерным распределением в интервале [-1,1]. Верхний индекс означает, что шаги заданы в виде столбца. Шаблон верхнего индекса выводится по цепочке View, Toolbars, Matrix или клавишами Ctrl+6.
|
| Задает цикл расчета перемещений
|
| Расчет перемещений для N частиц
|
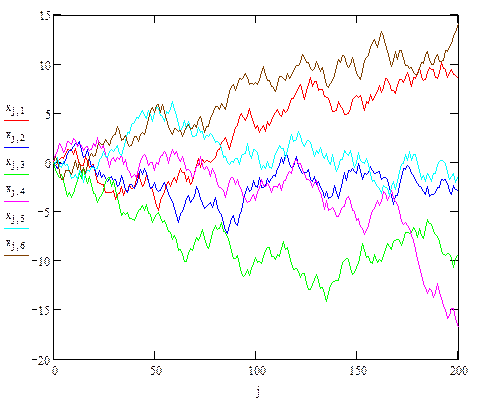
| Позволяет вывести на график все рассчитанные значения, включая 200-е
|
Очевидно, что параметрам "k" и "j" соответствуют значения времени в реальном процессе, так что построенные графики изображают зависимости местоположений частиц в выделенные моменты времени.
В следующем примере было взято N частиц, которые в начальный момент были равномерно распределены на оси "y", и для каждой их них был реализован процесс хаотического движения. Рисунок, отображающий положения частиц, действительно напоминает процесс их диффузии. Кроме того, был построен график зависимости среднего квадрата смещения от времени. Согласно формуле Эйнштейна зависимость должна быть линейной:  , где D – коэффициент диффузии (выбор значений коэффициентов см. Приложение в конце методички). И действительно, результаты численного эксперимента совпадают с теоретической зависимостью. Была также построена гистограмма распределения частиц по оси "x" и выполнено ее сравнение с теоретическим распределением.
, где D – коэффициент диффузии (выбор значений коэффициентов см. Приложение в конце методички). И действительно, результаты численного эксперимента совпадают с теоретической зависимостью. Была также построена гистограмма распределения частиц по оси "x" и выполнено ее сравнение с теоретическим распределением.
Основу расчета составил программный модуль Prog(step,particle). Модуль реализует step раз хаотическое движение частиц в количестве particle штук. Итогом расчета стал вектор конечных координат частиц и вектор, элементы которого содержат значения среднеквадратичного отклонений частиц от начального положения после 0, 1, 2,..., step шага.
Программа в MathCAD
| Проверка формулы Эйнштейна для процесса диффузии с коэффициентом 2D = 1/3
|
| Параметр, эквивалентный времени в реальном эксперименте
|
| Местоположение N частиц через step шагов. В исходном положении все частицы имели координаты x=0 и y = j. В процессе диффузии менялась координата x:
|
| Построение гистограммы распределения местоположения частиц
|
| Выбор сегментов разбиения
|
| Матрица гистограммы размера int x 2, состоящая из столбца сегментов разбиения и столбца частоты попадания в них данных
|
| Размер сегмента разбиения (берется из 1-го столбца матрицы f)
|
| Теоретическая зависимость
|
Приложение (краткие теоретические сведения)
Уравнение диффузии в одномерном случае:
 .
.
где c – концентрация частиц, D – коэффициент диффузии. Решением уравнения будет функция:
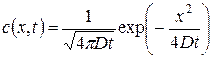 , с условием нормировки
, с условием нормировки  .
.
Такая нормировка позволяет рассматривать  как плотность вероятности нахождения диффундирующей частицы на расстоянии x от исходного местоположения через время t. Тогда для среднеквадратичного смещения получим соотношение (формула Эйнштейна):
как плотность вероятности нахождения диффундирующей частицы на расстоянии x от исходного местоположения через время t. Тогда для среднеквадратичного смещения получим соотношение (формула Эйнштейна):
 .
.
Сопоставим эту формулу с построенной моделью. Вспомним, что шаги смещения были заданы как случайные величины с равномерным распределением значений в интервале [-1,1]. Кроме того, полагалось, что время каждого шага составляло  (значения параметра
(значения параметра  ). Тогда из рекуррентной формулы программного модуля
). Тогда из рекуррентной формулы программного модуля  получим для среднего квадрата:
получим для среднего квадрата:
 .
.
Т.е. средний квадрат растет с каждым шагом на одинаковую величину  . При преобразовании было использовано свойство независимости значений
. При преобразовании было использовано свойство независимости значений 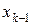 и
и  , так что
, так что  . Значение
. Значение  можно рассчитать по формуле
можно рассчитать по формуле  , где
, где  – плотность равномерного распределения случайной величины на отрезке [-1,1]. Итак, окончательно получим:
– плотность равномерного распределения случайной величины на отрезке [-1,1]. Итак, окончательно получим:
 .
.
Сравнивая эту формулу с формулой Эйнштейна, находим:  . Именно это значение было использовано при сравнительном анализе результатов численного эксперимента и теории.
. Именно это значение было использовано при сравнительном анализе результатов численного эксперимента и теории.
В условии нормировки функции  , приведенном выше, интегрирование можно приближенно заменить суммированием по малым интервалам
, приведенном выше, интегрирование можно приближенно заменить суммированием по малым интервалам  . Тогда доля частиц, оказавшихся вблизи координаты x в интервале
. Тогда доля частиц, оказавшихся вблизи координаты x в интервале  , будет:
, будет:
 .
.
При теоретическом анализе гистограммы полагалось  и
и 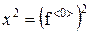 .
.
Задания для самостоятельного выполнения
1. Постройте рисунок с местоположением "N" частиц через "step" шагов, диффундирующих из начала координат в плоскости. Пример рисунка приведен ниже. N = 4000, step = 200.
2. Постройте такой же рисунок, но для 3-х мерной диффузии из начала координат.

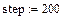






 , где D – коэффициент диффузии (выбор значений коэффициентов см. Приложение в конце методички). И действительно, результаты численного эксперимента совпадают с теоретической зависимостью. Была также построена гистограмма распределения частиц по оси "x" и выполнено ее сравнение с теоретическим распределением.
, где D – коэффициент диффузии (выбор значений коэффициентов см. Приложение в конце методички). И действительно, результаты численного эксперимента совпадают с теоретической зависимостью. Была также построена гистограмма распределения частиц по оси "x" и выполнено ее сравнение с теоретическим распределением.













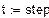



 .
.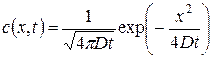 , с условием нормировки
, с условием нормировки  .
. как плотность вероятности нахождения диффундирующей частицы на расстоянии x от исходного местоположения через время t. Тогда для среднеквадратичного смещения получим соотношение (формула Эйнштейна):
как плотность вероятности нахождения диффундирующей частицы на расстоянии x от исходного местоположения через время t. Тогда для среднеквадратичного смещения получим соотношение (формула Эйнштейна): .
. (значения параметра
(значения параметра  ). Тогда из рекуррентной формулы программного модуля
). Тогда из рекуррентной формулы программного модуля  получим для среднего квадрата:
получим для среднего квадрата: .
. . При преобразовании было использовано свойство независимости значений
. При преобразовании было использовано свойство независимости значений 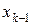 и
и  , так что
, так что  . Значение
. Значение  можно рассчитать по формуле
можно рассчитать по формуле  , где
, где  – плотность равномерного распределения случайной величины на отрезке [-1,1]. Итак, окончательно получим:
– плотность равномерного распределения случайной величины на отрезке [-1,1]. Итак, окончательно получим: .
. . Именно это значение было использовано при сравнительном анализе результатов численного эксперимента и теории.
. Именно это значение было использовано при сравнительном анализе результатов численного эксперимента и теории. , приведенном выше, интегрирование можно приближенно заменить суммированием по малым интервалам
, приведенном выше, интегрирование можно приближенно заменить суммированием по малым интервалам  . Тогда доля частиц, оказавшихся вблизи координаты x в интервале
. Тогда доля частиц, оказавшихся вблизи координаты x в интервале  , будет:
, будет: .
. и
и 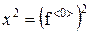 .
.
