Задачи для индивидуальных заданий

Типовой расчет № 2

ТЕМА: Аналитическая геометрия

Примеры решения задач.

Пример 1. В прямоугольной декартовой системе координат заданы вершины треугольника АВС: А (4; 3), В (16; –6); С (20; 16). Найти:

1. длину стороны АВ;
2. уравнения сторон АВ и ВС и их угловые коэффициенты;
3. угол В треугольника (с точностью до одной минуты);
4. уравнение высоты CD и ее длину;
5. уравнение биссектрисы BN;
6. уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD;
7. уравнение прямой KL, проходящей через точку K параллельно прямой АВ;
8. координаты точки М, расположенной симметрично точке А относительно прямой CD.

Построить треугольник АВС, высоту CD, медиану АЕ, биссектрису BN и точку М.

Решение.

1. Применяя формулу для вычисления расстояния между точками (или формулу для вычисления модуля вектора) находим:

.

2. Подставляя в уравнение прямой, проходящей через две точки, координаты точек А и В, В и С, получим уравнения:

В результате преобразования этих уравнений получим соответственно:

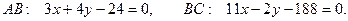
3. Если прямые не являются взаимно перпендикулярными и ни одна из них не параллельна оси Оу, то острый угол между ними может быть определен по формуле

.

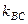Поскольку угловые коэффициенты сторон угла В нам уже известны и угол В острый угол (см. чертеж), то подставляя в последнюю формулу и , получим

.

Угол между прямыми может быть также найден как угол между их нормальными векторами (или между направляющими векторами).

 

4. Из условия перпендикулярности прямых АВ и СD находим угловой коэффициент прямой CD: 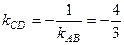. Если известна точка искомой прямой и ее угловой коэффициент k, то уравнение прямой можно записать в виде 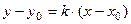. Поскольку координаты точки С нам известны, то уравнение прямой СD имеет вид:

.

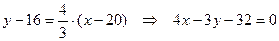Для нахождения длины высоты CD определим вначале координаты точки D – точки пересечения прямых AB и CD. Решая систему уравнений

находим . Поэтому .

Длину высоты CD можно найти по формуле, дающей расстояние от точки до прямой:

 

 

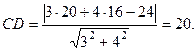
5. Вначале определим координаты точки N, принадлежащей стороне треугольника АС, и делящей эту сторону в отношении . По свойству биссектрисы угла треугольника можем записать . Вычисляем длины сторон треугольника: . Условимся проводить вычисления в этом пункте с точностью до 0,1, т.е. . Находим координаты точки N:

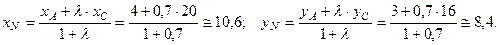
Запишем уравнение биссектрисы угла В как уравнение прямой, проходящей через две точки В (16; –6) и N (10,6; 8,4):

–уравнение биссектрисы угла В.

Можно рекомендовать другой путь решения этой задачи: найти орт вектора , т.е. , и орт вектора , т.е. 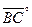, тогда вектор есть направляющий вектор искомой биссектрисы, проходящей через заданную точку В.

 

6. Определим координаты точки Е, являющейся серединой стороны ВС, по формулам деления отрезка в данном отношении при :

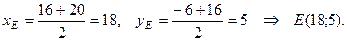
Согласно уравнению прямой, проходящей через две точки, уравнение медианы АЕ имеет вид:

или – общее уравнение прямой АЕ.

Точка пересечения медианы АЕ и высоты CD определяется в результате решения системы уравнений

7. Ввиду параллельности прямых KL и AB, . Подставляя координаты точки К и в уравнение прямой, проходящей через заданную точку, с известным угловым коэффициентом, получим

– общее уравнение прямой KL.

8. Прямая АВ перпендикулярна прямой CD; поэтому точка М лежит на прямой АВ. Кроме того, точка D является серединой отрезка АМ. Применяя формулы деления отрезка в данном отношении, находим координаты точки М:

Выполним чертеж:

 

 

 

Пример 2. Привести уравнение линии второго порядка к каноническому виду; построить данную линию (на чертеже указать «старую» и «новую» системы координат).

Решение. Перепишем уравнение в виде

.

Проведем в скобках «дополнение до полного квадрата» и выполним очевидные преобразования:

,

,

,

.

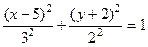Введем «новые» координаты . Последнее уравнение в «новых» координатах примет вид:

.

Это есть каноническое уравнение эллипса с полуосями

 

 

Пример 3. В прямоугольной декартовой системе координат заданы четыре точки . Требуется:

1. составить общее уравнение плоскости Q, проходящей через точки А, В, С;
2. составить канонические уравнения прямой линии, проходящей через точку М перпендикулярно плоскости Q и найти координаты точки N пересечения этой прямой с плоскостью Q;
3. найти расстояние от точки М до плоскости Q;
4. составить канонические уравнения прямых АВ и АМ и найти угол между этими прямыми;
5. найти угол между прямой АМ и плоскостью Q;
6. найти площадь треугольника АВС;
7. найти объем пирамиды АВСМ.

Решение.

1. Подставляя в уравнение плоскости, проходящей через три заданные точки, координаты точек А, В, С получим

.

В результате вычисления определителя имеем

.

Искомое уравнение плоскости Q:

.

Уравнение плоскости Q можно найти используя другие формулы, например: уравнение плоскости, проходящей через точку, ортогонально вектору (здесь в качестве заданной точки взять любую из трех заданных точек, скажем точку А, и нормальный вектор плоскости Q определить как векторное произведение векторов и ).

 

2. В качестве направляющего вектора искомой прямой возьмем нормальный вектор плоскости Q. Подставив в канонические уравнения прямой координаты точки М и координаты направляющего вектора (2, –1, –2), получим уравнения прямой MN:

.

Найдем точку N. Используем параметрические уравнения прямой MN

Подставляя эти выражения в уравнение плоскости Q, получим значение параметра t:

.

Подставив в параметрические уравнения прямой MN , находим координаты точки N пересечения этой прямой с плоскостью Q: .

 

3. Используя формулу для нахождения расстояния от точки до плоскости, находим:

.

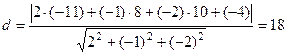Это расстояние можно найти и как расстояние между двумя точками: М и N.

 

4. Запишем уравнение прямой АВ как уравнение прямой, проходящей через две точки

канонические уравнения прямой АВ: .

Аналогично получаем канонические уравнения прямой АМ: .

Угол между прямыми АВ и АМ найдем как угол между их направляющими векторами:

,

поскольку , то мы находим острый угол между этими прямыми: (с точностью до минуты).

 

5. В формулу для вычисления синуса угла между прямой и плоскостью подставляем координаты нормального вектора плоскости и направляющего вектора прямой, получим:

(с точностью до одной минуты).

 

6. Поскольку площадь параллелограмма, построенного на векторах и , численно равна модулю векторного произведения этих векторов, то площадь треугольника АВС найдем как

.

.

Следовательно, кв.ед.

 

7.) , здесь смешанное произведение трех векторов.

Следовательно, куб.ед.

Конечно, в данном случае можно найти объем пирамиды и так: 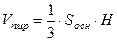, т.е.

Задачи для индивидуальных заданий

 

В задачах 1-30даны координаты вершин треугольника АВС. Найти:

1) уравнение биссектрисы, проведенной из вершины В;

2) центр тяжести треугольника (точка пересечения медиан);

3) центр и уравнение описанной окружности;

4) площадь треугольника АВС;

5) записать систему линейных неравенств, определяющих треугольник АВС.

 

№
А	-3,-1	-4,2	1,-1	-2,-3	1,-4	-4,1	-1,2	-3,-2	3,2	-1,-3	-1,-3	2,-1	-1,-3	3,2	-1,2
B	-1,3	2,3	3,-1	-1,-3	-4,2	-4,-1	-3,-1	-4,2	-1,-1	-1,-2	2,3	2,1	1,-1	2,-4	-4,2
C	-4,3	-4,-2	-1,3	2,-1	-4,-3	1,-1	2,-2	-1,-1	-3,-2	1,-1	-4,-1	-2,3	-3,-4	-1,-4	-1,-3

 

№
А	-4,-1	2,-1	-1,2	-4,-1	-4,-4	-4,-2	-4,1	-2,-4	-2,1	-2,-4	-4,1	3,2	2,-1	1,-1	-3,-2
B	-1,-2	3,-2	-1,-4	1,-1	-1,-3	-4,1	3,-4	-1,1	-1,-2	-1,1	-4,-1	2,-4	3,-2	3,-1	-4,2
C	-4,-3	1,2	1,-4	-4,1	-4,-1	-2,-1	2,-3	2,2	-1,-4	2,2	1,-1	-1,-4	1,2	-1,3	-1,-1

 

В задачах 31-60 привести уравнения линий 2 – го порядка к каноническому виду; построить данные линии (на чертеже указать «старую» и «новую» системы координат).

 

 

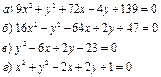
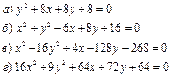
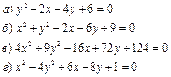
В задачах 61-90 даны координаты вершин пирамиды . Найти:

1) канонические уравнения прямой ;

2) косинус угла между ребрами и ;

3) общее уравнение плоскости ;

4) синус угла между ребром и гранью ;

5) площадь грани ;

6) объем пирамиды;

 

№
А	-1,1,1	-4,-4,1	-4,3,-1	1,-3,-1	-2,-4,-1	3,-4,-4	-4,-1,-4	1,-2,-4	-1,-4,-4	-4,-4,-1
В	-2,-4,-4	-1,-3,-1	-4,-2,-2	3,-3,-1	-1,1,-3	-1,3,-2	-4,1,-4	-1,-3,-4	-3,-1,1	3,-2,-4
С	-3,-4,-2	-3,-4,-4	-4,1,-4	2,-1,-3	1,-3,-4	1,3,-4	-3,-4,-1	-4,1,3	2,-3,-4	-4,-4,1
D	2,-1,1	-3,-1,-1	3,-1,2	1,-4,-2	-2,3,-1	-4,-4,1	-4,-3,-3	1,-3,-4	-1,-3,3	-3,3,-2

 

№
А	-1,-1,-4	2,-1,3	1,-1,-4	-4,-4,1	-4,-3,-1	3,3,3	1,-4,1	1,-2,-1	-4,1,-4	-2,-4,-1
В	-2,3,1	-2,-1,-4	3,-1,-1	3,-2,-1	-3,-1,3	-3,2,-3	-1,-1,2	-4,-4,2	-4,-1,-4	3,2,-1
С	1,-4,3	-4,3,-1	-4,-4,-2	-2,-1,-1	2,2,2	-3,-2,2	-1,1,-4	3,-4,-4	-2,-4,-3	-1,-4,-4
D	-3,3,-4	-4,-4,-4	1,1,-4	-4,2,1	1,2,-4	-2,3,-4	-1,-4,1	3,-4,2	-4,-1,3	3,3,-2

 

№
А	-2,-4,-4	-4,-1,-1	2,-4,1	-4,-1,-4	-4,-1,-4	-4,1,-4	-1,-4,-4	-1,-1,-4	-4,-1,-1	-4,-4,1
В	-4,-4,-1	2,-4,1	-4,2,-2	-4,-2,2	-4,1,-4	-4,-1,-4	-3,-1,1	-2,3,1	2,-4,1	3,-2,-1
С	-4,-1,-1	-1,-1,-4	-1,2,-1	1,-4,-2	-3,-4,-1	-2,-4,-3	2,-3,-4	1,-4,3	-1,-1,-4	-2,-1,-1
D	1,2,1	-4,2,-4	-1,-1,2	-4,-3,-1	-4,-3,-3	-4,-1,3	-1,-3,3	-3,3,-4	-4,2,-4	-4,2,1