Используя данные Федеральной службы государственной статистики России (за двенадцать месяцев) из периода 2004 - 2005гг., следует:
1. Оценить влияние факторов (X1, X2, X3, X4, X5, X6, X7, X8) на изучаемый показатель (Y) и друг на друга с помощью коэффициентов линейной корреляции
Таблица 1.
| в% к предыдущему периоду | индексы цен платных услуг | индексы цен производителей | добыча полезных ископаемых | обрабатывающие производства | производство и распределение электроэнергии газа и воды | индексы тарифов на грузовые перевозки | железнодорожный транспорт | автомобильный транспорт | трубопроводный транспорт |
| Y | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | |
| ицпу | пр | дпи | оп | прэгв | гп | жт | ат | тт | |
| июл.04 | 101,3 | 101,2 | 102,9 | 100,7 | 100,1 | 102,1 | 101,3 | ||
| авг.04 | 101,8 | 103,9 | 101,4 | 100,2 | 100,2 | 100,4 | |||
| сен.04 | 100,6 | 103,1 | 103,1 | 100,3 | 101,9 | 100,6 | |||
| окт.04 | 101,2 | 101,8 | 103,6 | 101,4 | 99,9 | 95,4 | 101,5 | 87,4 | |
| ноя.04 | 100,8 | 104,5 | 101,5 | 100,7 | 101,9 | 101,1 | |||
| дек.04 | 100,1 | 100,8 | 99,8 | 99,9 | 102,1 | 100,6 | 105,8 | ||
| янв.05 | 108,8 | 100,5 | 95,7 | 100,9 | 104,9 | 113,9 | 108,8 | 103,2 | 122,6 |
| фев.05 | 102,2 | 101,3 | 98,4 | 100,9 | 106,3 | 100,1 | 100,8 | 100,1 | |
| мар.05 | 101,2 | 102,5 | 109,6 | 100,3 | 100,3 | 99,9 | |||
| апр.05 | 100,8 | 102,5 | 108,9 | 101,1 | 100,3 | 103,5 | 107,7 | ||
| май.05 | 100,8 | 102,7 | 109,7 | 100,1 | 100,3 | 100,5 | |||
| июн.05 | 100,9 | 100,1 | 99,3 | 100,3 | 100,1 | 101,7 | 100,6 | 103,7 |
Коэффициент линейной корреляции, с помощью которого можно оценить влияние факторов (X1, X2, X3, X4, X5, X6, X7, X8) на изучаемый показатель (Y) и друг на друга, вычисляется по формуле:
,
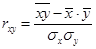где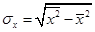 
- среднее квадратическое отклонение фактора 
.
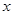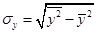- среднее квадратическое отклонение изучаемого показателя 
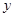. Если 
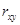=0, то факторы не могут влиять на изучаемый показатель, так как связь между ними будет отсутствовать. Чем ближе 
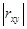к 1, тем сильнее связь между факторами и изучаемым показателем. Рассмотрим сначала как влияет X1 на изучаемый показатель Y. Произведем предварительные расчеты в таблице:
Таблица 2.
| 
| 
| 
| 
| |
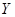
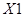
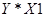
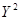
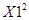
| июл.04 | 101,3 | 101,2 | 10251,56 | 10261,69 | 10241,44 |
| авг.04 | 101,8 | 10281,8 | 10363,24 | ||
| сен.04 | 100,6 | 103,1 | 10371,86 | 10120,36 | 10629,61 |
| окт.04 | 101,2 | 101,8 | 10281,6 | 10241,44 | 10363,24 |
| ноя.04 | 100,8 | 10281,6 | 10160,64 | ||
| дек.04 | 100,1 | 10110,1 | 10020,01 | ||
| янв.05 | 108,8 | 100,5 | 10934,4 | 11837,44 | 10100,25 |
| фев.05 | 102,2 | 101,3 | 10352,86 | 10444,84 | 10261,69 |
| мар.05 | 101,2 | 102,5 | 10241,44 | 10506,25 | |
| апр.05 | 100,8 | 102,5 | 10160,64 | 10506,25 | |
| май.05 | 100,8 | 102,7 | 10352,16 | 10160,64 | 10547,29 |
| июн.05 | 100,9 | 100,1 | 10100,09 | 10180,81 | 10020,01 |
| Сумма | 1220,6 | 1219,6 | 124023,03 | 124211,94 | 123963,3 |
| Среднее значение | 101,71667 | 101,6333 | 10336,96666 | 10350,995 | 10330,27 |
Из таблицы находим среднее квадратическое отклонение фактора :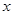
= 
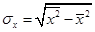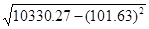=0,9679876;
среднее квадратическое отклонение изучаемого показателя :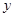
= 
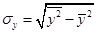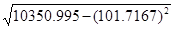=2,1718655.
Полученные значения подставляем в формулу:
= 
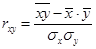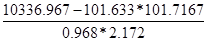=-0,41056
Коэффициент линейной корреляции равен 0,3 ≤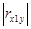 
= 
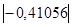≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором 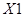умеренная.
Аналогично оценивается влияние остальных факторов на изучаемый показатель (Y).
= 
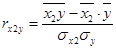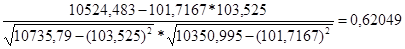
Коэффициент линейной корреляции равен 0,3 ≤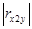 
= 
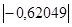≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х2 умеренная.
= 
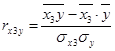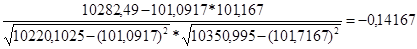
Коэффициент линейной корреляции равен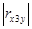 
= 
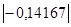< 0,3. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х3 слабая.
= 
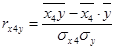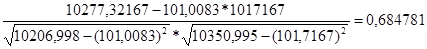
Коэффициент линейной корреляции равен 0,3 ≤ =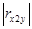 
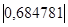≤0,7. Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х4 умеренная.
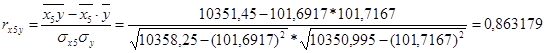
Коэффициент линейной корреляции равен 0,7 <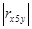 
= 
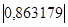Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х5 близка к линейной (тесная).
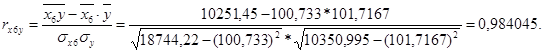
Коэффициент линейной корреляции равен 0,7 <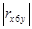 
= 
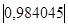Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х6 близка к линейной (тесная).
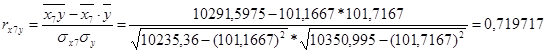
Коэффициент линейной корреляции равен 0,7 <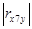 
= 
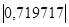Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х7 близка к линейной (тесная).
Коэффициент линейной корреляции равен 0,7 <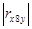 
= 
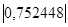Это говорит о том, что связь между изучаемым показателем (Y) и фактором Х8 близка к линейной (тесная).
Влияние факторов друг на друга рассчитывается аналогично. Все полученные данные представим в таблице.
Таблица 3.
| Y | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | |
| Y | |||||||||
| X1 | -0,41056 | ||||||||
| X2 | -0,62049 | 0,817335 | |||||||
| X3 | -0,14167 | 0,750202 | 0,304572 | ||||||
| X4 | 0,684791 | -0,31544 | -0,63666 | -0,13627 | |||||
| X5 | 0,863179 | -0,39974 | -0,4795 | -0,21126 | 0,494364 | ||||
| X6 | 0,984045 | -0,36981 | -0,55741 | -0,09167 | 0,560132 | 0,89804 | |||
| X7 | 0,719717 | -0,08272 | -0,45151 | 0,36154 | 0,360766 | 0,610648 | 0,762909 | ||
| X8 | 0,752448 | -0,40384 | -0,42926 | -0,26069 | 0,440197 | 0,978356 | 0,790727 | 0,493109 |
Из свойств корреляции известно, что если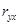 
> 0, то связь прямая (
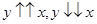); если 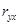< 0, то связь обратная 
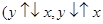). Факторы (Х1), (Х3), (Х2) имеют обратную связь с ицпу, то есть если индекс цен платных услуг растет, они падают, и наоборот. Факторы (Х4), (Х5), (Х6), (Х7), (Х8) имеют прямую связь с индексом цен платных услуг (вместе с ним растут или падают).
Самая сильная связь наблюдается между индексом цен платных услуг и железнодорожным транспортом. Самая слабая связь наблюдается между обрабатывающим производством и производством и распределением электроэнергии, газа и воды.