При процедуре выбора факторов должны выполняться следующие условия:
Факторы должны быть количественно измеримы или допускать кодировку. В нашем случае это условие выполняется.
Факторы должны "объяснять" поведение изучаемого показателя согласно принятым положениям экономической теории. Это должно подтверждаться индексами корреляции факторов с показателями. Это условие тоже выполняется, так как для всех факторов индексы корреляции рассчитаны.
Факторы не должны находиться в точной функциональной связи (допустим, коллинеарной). Включение в модель факторов с индексами корреляции, близкими по модулю к единице может привести к нежелательным последствиям:
1) факторы будут дублировать друг друга, и будет затруднена экономическая интерпретация параметров модели;
2) система уравнений для определения параметров может оказаться плохо обусловленной и повлечь ненадежность полученных уравнений регрессии т нежелательность их использования для анализа и прогноза.
При наличии корреляции ≥0,7 между факторами один из них следует исключить. Оставить рекомендуется тот, который при достаточно тесной связи с показателем имеет более слабую связь с другими факторами.
Рассмотрим таблицу 3, используя метод исключения, отберем факторы для построения регрессионных моделей. Так как связь между факторами должна быть слабой, исключим все факторы, коэффициент корреляции которых больше или равен по модулю 0,3. Для построения модели оставляем факторы сильно или умеренно влияющие на данный показатель, то есть коэффициент корреляции должен быть больше или равен 0,3.
Следующее необходимое условие при построении регриссионных моделей: Число включаемых факторов должно в 6 раз меньше объема наблюдений, по которым строится регрессия. N-число наблюдений в нашем случае равно 12. Тогда m ≤  , то есть m=1 или m=2.
, то есть m=1 или m=2.
Число параметров при факторах в линейной модели совпадают с их количеством: m=p.
Итак, можно предложить следующие регрессионные модели:
1. 
2. 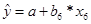 .
.
3.  .
.
Используя инструмент РЕГРЕССИЯ, оценим 1 модель.
1 этап. Оценка значимости модели в целом.
Таблица 4.
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,985324602 | ||||
| R-квадрат | 0,970864572 | ||||
| Нормированный R-квадрат | 0,963580715 | ||||
| Стандартная ошибка | 0,453164887 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 54,74441 | 27,3722 | 133,289901 | 0,00000072 | |
| Остаток | 1,642867 | 0, 205358 | |||
| Итого | 56,38727 | ||||
Модель линейной регрессии с двумя фактором Х1 и X6 значима в целом согласно F-критерию (F=133,2899) с приемлемым уровнем значимости 0,00000072 ≤ 0,05
Итак, получаем модель

| |||||
| Коэф-ты | Станд. ошибка | t-стат. | P-Значение | ||
| Y-пересечение | 27,18887556 | 17,92439 | 1,516864 | 0,16777466 | |
| Х1 | -0,1220023 | 0,146648 | -0,83194 | 0,42957614 | |
| Х6 | 0,86279739 | 0,058131 | 14,84242 | 0,000000418 |
Согласно критерию Стьюдента 2 параметра модели a=27,18 и 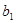 =-0,122 незначимы с приемлемыми уровнями
=-0,122 незначимы с приемлемыми уровнями  >0,05 и
>0,05 и 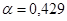 >0,05. Следовательно, эта модель неудачна и не может быть использована к анализу и прогнозу индекса цен платных услуг. Следует изменить спецификацию модели (необходимо убрать фактор Х1).
>0,05. Следовательно, эта модель неудачна и не может быть использована к анализу и прогнозу индекса цен платных услуг. Следует изменить спецификацию модели (необходимо убрать фактор Х1).
Используя инструмент РЕГРЕССИЯ, оценим 2 модель.
1 этап. Оценка значимости модели в целом.
Таблица 5.
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,984045 | ||||
| R-квадрат | 0,968344 | ||||
| Нормированный R-квадрат | 0,964827 | ||||
| Стандартная ошибка | 0,445346 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 54,60227273 | 54,60227 | 275,3055768 | 0,0000000468 | |
| Остаток | 1,785 | 0, 198333 | |||
| Итого | 56,38727273 | ||||
Модель линейной регрессии с фактором X6 значима в целом согласно F-критерию (F=275,306) с приемлемым уровнем значимости 0,0000000468 ≤ 0,05
Итак, получаем модель
 2 этап. Оценка параметров модели.
2 этап. Оценка параметров модели.
| |||||
| Коэф-ты | Станд. ошибка | t-стат. | P-Значение | ||
| Y-пересечение | 12,98182 | 5,351909883 | 2,425642 | 0,038255004 | |
| X6 | 0,880682 | 0,05307763 | 16,59233 | 0,0000000468 |
Согласно критерию Стьюдента 2 параметра модели a=12,98 и b=0,88 значимы с приемлемыми уровнями  <0,05 и
<0,05 и 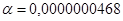 <0,05.
<0,05.
3 этап. Проверка наличия необходимых свойств у остатка модели.
Таблица 6.
| ВЫВОД ОСТАТКА | |||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 101,05 | -0,05 | -0,118345267 | |
| 101,05 | -0,45 | -1,065107404 | |
| 101,05 | 0,15 | 0,355035801 | |
| 101,05 | -0,25 | -0,591726335 | |
| 101,05 | -0,05 | -0,118345267 | |
| 108,8 | 0,00000000000132 | 0,000000000003128 | |
| 101,05 | 1,15 | 2,721941143 | |
| 101,05 | 0,15 | 0,355035801 | |
| 101,05 | -0,25 | -0,591726335 | |
| 101,05 | -0,25 | -0,591726335 | |
| 101,05 | -0,15 | -0,355035801 |
График 1.

Проверяем случайность остатков Первое, что требуется, это чтобы график остатков располагался в горизонтальной полосе, симметричной относительно оси абсцисс. Согласно предпосылкам МНК возмущение должно быть случайной величиной с нулевым математическим ожиданием. Это имеет место для получения однофакторной регрессии. График остатка (возмущения, ошибки) располагается в горизонтальной полосе. Имеется большое количество локальных экстремумов (максимумов и минимумов).  -значит остатки случайные.
-значит остатки случайные.
Согласно следующей предпосылке остатки должны быть равноизменчивы. Для проверки этой предпосылки используем в Microsoft Excel инструмент "Среднее значение".


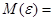 -0,000000000000006
-0,000000000000006  .
.
Проверка на гомоскедастичность по методу Гольдфельда-Квандта невозможна, так как недостаточно наблюдений (должно быть n>12m) /
Проверим отсутствие автокорреляции остатков. Для этого чаще всего используют критерий Дарбина Уотсона (d-критерий):
 .
.
 находится в Microsoft Excel при помощи инструмента "СУММКВРАЗН"
находится в Microsoft Excel при помощи инструмента "СУММКВРАЗН"
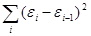 =3,215
=3,215
 , берется из таблицы 4.1 "SS"/ "остаток"
, берется из таблицы 4.1 "SS"/ "остаток"
 1,785
1,785
d=  .
.
Критерий Дарбина Уотсона (d-критерий): n=12, m=1,  , dl=0,97,du=1,33
, dl=0,97,du=1,33
I dl II du III IV 4-du V 4-dl VI
 0 0,97 1,33 2 2,67 3,03 4
0 0,97 1,33 2 2,67 3,03 4
d=1,801 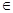 III, IV. Значит нет оснований отклонить предположение об отсутствии автокорреляции соседних остатков по d-критерию с уровнем значимости
III, IV. Значит нет оснований отклонить предположение об отсутствии автокорреляции соседних остатков по d-критерию с уровнем значимости  .
.
Следующее необходимое условие: остатки должны иметь распределение Гаусса. можно ограничиться критерием размахов (RS - критерий).
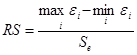 .
.
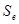 -стандартная ошибка модели
-стандартная ошибка модели
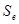 =0,445346.
=0,445346.
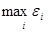 находится в Microsoft Excel при помощи функции "МАКС".
находится в Microsoft Excel при помощи функции "МАКС".
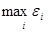 =1,15.
=1,15.
 находится в Microsoft Excel при помощи функции "МИН".
находится в Microsoft Excel при помощи функции "МИН".
 =-0,45.
=-0,45.
RS=3,59
Критерий размахов, RS - критерий: n=12, α =0,05, a=2,8, b=3,91.
Если a <RS < b, то остатки имеют нормальный закон распределения с уровнем α =0,05.
2,8 <3,59 < 3,91.
Вывод: Все предпосылки регрессионного анализа выполняются с уровнем α =0,05. Значит модель успешно прошла проверку оценки ее качества.
Используя инструмент РЕГРЕССИЯ, оценим 3 модель.
1 этап. Оценка значимости модели в целом.
Таблица 7.
| ВЫВОД ИТОГОВ | |||||
| Регрессионная статистика | |||||
| Множественный R | 0,863178866 | ||||
| R-квадрат | 0,745077754 | ||||
| Нормированный R-квадрат | 0,71675306 | ||||
| Стандартная ошибка | 1,263784889 | ||||
| Наблюдения | |||||
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 42,01290252 | 42,0129 | 26,30488273 | 0,000620555 | |
| Остаток | 14,37437021 | 1,597152 | |||
| Итого | 56,38727273 | ||||
Модель линейной регрессии с фактором X5 значима в целом согласно F-критерию (F=26,304) с приемлемым уровнем значимости 0,0000000468 ≤ 0,05
Итак, получаем модель

| |||||
| Коэф-ты | Станд. ошибка | t-стат. | P-Значение | Нижние 95% | |
| Y-пересечение | 55,68196551 | 8,991138974 | 6, 192982 | 0,00016021 | 35,34258057 |
| Х5 | 0,453226954 | 0,088368512 | 5,128829 | 0,000620555 | 0,253323338 |
Согласно критерию Стьюдента 2 параметра модели a=55,68 и b=0,453 значимы с приемлемыми уровнями  <0,05 и
<0,05 и  <0,05.
<0,05.
3 этап. Проверка наличия необходимых свойств у остатка модели.
Таблица 8.
| ВЫВОД ОСТАТКА | |||
| Наблюдение | Предсказанное 101,3 | Остатки | Стандартные остатки |
| 101,0953062 | -0,095306249 | -0,079492648 | |
| 101,1406289 | -0,540628945 | -0,450925589 | |
| 98,91981687 | 2,280183127 | 1,901845857 | |
| 101,3219197 | -0,521919726 | -0,43532068 | |
| 101,9564375 | -0,956437461 | -0,797741462 | |
| 107,3045155 | 1,495484488 | 1,247347611 | |
| 101,0499836 | 1,150016446 | 0,959201034 | |
| 101,0046609 | 0, 195339141 | 0,162927675 | |
| 102,5909552 | -1,790955196 | -1,493792616 | |
| 101,1406289 | -0,340628945 | -0,284110403 | |
| 101,7751467 | -0,87514668 | -0,729938779 |
График 2.

Проверяем случайность остатков. Согласно предпосылкам МНК возмущение должно быть случайной величиной с нулевым математическим ожиданием. Это имеет место для получения однофакторной регрессии. График остатка (возмущения, ошибки) располагается в горизонтальной полосе. Имеется большое количество локальных экстремумов (максимумов и минимумов).  -значит остатки случайные.
-значит остатки случайные.
Согласно следующей предпосылке остатки должны быть равно изменчивы. Для проверки этой предпосылки используем в Microsoft Excel инструмент "Среднее значение".


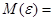 -0,0000000000000026
-0,0000000000000026  .
.
Проверка на гомоскедастичность по методу Гольдфельда-Квандта невозможна, так как недостаточно наблюдений (должно быть n>12m) /
Проверим отсутствие автокорреляции остатков. Для этого чаще всего используют критерий Дарбина Уотсона (d-критерий):
 .
.
 находится в Microsoft Excel при помощи инструмента "СУММКВРАЗН"
находится в Microsoft Excel при помощи инструмента "СУММКВРАЗН"
 =29,573
=29,573
 , берется из таблицы 4.1 "SS"/ "остаток"
, берется из таблицы 4.1 "SS"/ "остаток"
 14,374
14,374
d=  .
.
Критерий Дарбина Уотсона (d-критерий): n=12, m=1,  , dl=0,97,du=1,33
, dl=0,97,du=1,33
 I dl II du III IV 4-du V 4-dl VI
I dl II du III IV 4-du V 4-dl VI
0 0,97 1,33 2 2,67 3,03 4
d=2,057  III, IV. Значит нет оснований отклонить предположение об отсутствии автокорреляции соседних остатков по d-критерию с уровнем значимости
III, IV. Значит нет оснований отклонить предположение об отсутствии автокорреляции соседних остатков по d-критерию с уровнем значимости 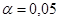 . Следующее необходимое условие: остатки должны иметь распределение Гаусса. можно ограничиться критерием размахов (RS - критерий).
. Следующее необходимое условие: остатки должны иметь распределение Гаусса. можно ограничиться критерием размахов (RS - критерий).
 .
.
 -стандартная ошибка модели
-стандартная ошибка модели
 =1,263784889.
=1,263784889.
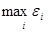 находится в Microsoft Excel при помощи функции "МАКС".
находится в Microsoft Excel при помощи функции "МАКС".
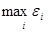 =.2,280183127
=.2,280183127
 находится в Microsoft Excel при помощи функции "МИН".
находится в Microsoft Excel при помощи функции "МИН".
 =-1,790955196
=-1,790955196
RS=3,22138
Критерий размахов, RS - критерий: n=12, α =0,05, a=2,8, b=3,91.
Если a <RS < b, то остатки имеют нормальный закон распределения с уровнем α =0,05.
2,8 <3,22138 < 3,91.
Вывод: Все предпосылки регрессионного анализа выполняются с уровнем α =0,05. Значит модель успешно прошла проверку оценки ее качества.