Попытка криптоанализа называется вскрытием. Основное предположение криптоанализа, впервые сформулированное в девятнадцатом веке Датчманом А. Кирхгофом (Dutchman A. Kerckhoffs), и состоит в том, что безопасность полностью определяется ключом. Кирхгоф предполагает, что у криптоаналитика есть полное описание алгоритма и его реализации. Хотя в реальном мире криптоаналитики не всегда обладают подробной информацией, такое предположение является хорошей рабочей гипотезой. Если противник не сможет взломать алгоритм, даже зная, как он работает, то тем более враг не сможет вскрыть алгоритм без этого знания. Ниже перечислены основные типы криптоаналитического вскрытия. Для каждого из них, конечно, предполагается, что криптоаналитик обладает всей полнотой знания об используемом алгоритме шифрования:
· Вскрытие с использованием только шифротекста. У криптоаналитика есть шифротексты нескольких сообщений, зашифрованных одним и тем же алгоритмом шифрования. Задача криптоаналитика состоит в раскрытии открытого текста как можно большего числа сообщений или, что лучше, получении ключа (ключей), использованного для шифрования сообщений, для дешифрировании других сообщений, зашифрованных теми же ключами.
· Вскрытие с использованием открытого текста. У криптоаналитика есть доступ не только к шифротекстам нескольких сообщений, но и к открытому тексту этих сообщений. Его задача состоит в получении ключа (или ключей), использованного для шифрования сообщений, для дешифрировании других сообщений, зашифрованных тем же ключом (ключами).
· Вскрытие с использованием выбранного открытого текста. У криптоаналитика не только есть доступ к шифротекстам и открытым текстам нескольких сообщений, но и возможность выбирать открытый текст для шифрования. Это предоставляет больше вариантов чем вскрытие с использованием открытого текста, так как криптоаналитик может выбирать шифруемые блоки открытого текста, что может дать больше информации о ключе. Его задача состоит в получении ключа (или ключей), использованного для шифрования сообщений, или алгоритма, позволяющего дешифрировать новые сообщения, зашифрованные тем же ключом (или ключами).
· Адаптивное вскрытие с использованием открытого текста. Это частный случай вскрытия с использованием выбранного открытого текста. Криптоаналитик не только может выбирать шифруемый текст, но также может строить свой последующий выбор на базе полученных результатов шифрования. При вскрытии с использованием выбранного открытого текста криптоаналитик мог выбрать для шифрования только один большой блок открытого текста, при адаптивном вскрытии с использованием выбранного открытого текста он может выбрать меньший блок открытого текста, затем выбрать следующий блок, используя результаты первого выбора и так далее.
· Вскрытие с использованием выбранного шифротекста. Криптоаналитик может выбрать различные шифротексты для дешифрирования и имеет доступ к дешифрированным открытым текстам. Например, у криптоаналитика есть доступ к "черному ящику", который выполняет автоматическое дешифрирование. Его задача состоит в получении ключа.
· Вскрытие с использованием выбранного ключа. Такой тип вскрытия означает не то, что криптоаналитик может выбирать ключ, а что у него есть некоторая информация о связи между различными ключами. Это странный, запутанный и не очень практичный тип вскрытия.
· Бандитский криптоанализ. Криптоаналитик угрожает, шантажирует или пытает кого-нибудь, пока не получит ключ. Взяточничество иногда называется вскрытием с покупкой ключа. Это очень мощные способы вскрытия, часто являющиеся наилучшим путем взломать алгоритм.
Вскрытия с известным открытым текстом и с использованием выбранного открытого текста встречаются чаще, чем можно подумать. Не является невозможным для криптоаналитика добыть открытый текст шифрованного сообщения или подкупить кого-нибудь, кто зашифрует выбранное сообщение. Многие сообщения имеют стандартные начало и окончание, что может быть известно криптоаналитику. Особенно уязвим шифрованный исходный код из-за частого использования ключевых слов: #define, struct, else, return. Те же проблемы и у шифрованного исполнимого кода: функции, циклические структуры и так далее. Вскрытия с известным открытым текстом (и вскрытия с выбранным шифротекстом) успешно использовались в борьбе с немцами и японцами в ходе Второй мировой войны.
Безопасность алгоритмов
Различные алгоритмы предоставляют различные степени безопасности в зависимости от того, насколько трудно взломать алгоритм. Если стоимость взлома алгоритма выше, чем стоимость зашифрованных данных, вы, скорее всего, в безопасности. Если время взлома алгоритма больше, чем время, в течение которого зашифрованные данные должны сохраняться в секрете, то вы также, скорее всего, в безопасности. Если объем данных, зашифрованных одним ключом, меньше, чем объем данных, необходимый для взлома алгоритма, и тогда вы, скорее всего, в безопасности. Ларе Кнудсен (Lars Knudsen) разбил вскрытия алгоритмов по следующим категориям, приведенным в порядке убывания значимости:
· Полное вскрытие. Криптоаналитик получил ключ.
· Глобальная дедукция. Криптоаналитик получил альтернативный алгоритм, А, эквивалентный вашему без знания ключа.
· Местная (или локальная) дедукция. Криптоаналитик получил открытый текст для перехваченного шифротекста.
· Информационная дедукция. Криптоаналитик получил некоторую информацию о ключе или открытом тексте. Такой информацией могут быть несколько бит ключа, сведения о форме открытого текста и так далее.
Алгоритм является безусловно безопасным, если, независимо от объема шифротекстов у криптоаналитика, информации для получения открытого текста недостаточно. По сути, только шифрование одноразовыми блокнотами невозможно вскрыть при бесконечных ресурсах. Все остальные криптосистемы подвержены вскрытию с использованием только шифротекста простым перебором возможных ключей и проверкой осмысленности полученного открытого текста. Это называется вскрытием грубой силой. Криптография больше интересуется криптосистемами, которые тяжело взломать вычислительным способом. Алгоритм считается вычислительно безопасным (или, как иногда называют, сильным), если он не может быть взломан с использованием доступных ресурсов сейчас или в будущем. Термин "доступные ресурсы" является достаточно расплывчатым. Сложность вскрытия можно измерить различными способами:
· Сложность данных Объем данных, используемых на входе операции вскрытия.
· Сложность обработки. Время, нужное для проведения вскрытия. Часто называется коэффициентом работы.
· Требования к памяти. Объем памяти, необходимый для вскрытия.
В качестве эмпирического метода сложность вскрытия определяется по максимальному из этих трех коэффициентов. Ряд операций вскрытия предполагают взаимосвязь коэффициентов: более быстрое вскрытие возможно за счет увеличения требований к памяти. Сложность выражается порядком величины. Если сложность обработки для данного алгоритма составляет 2128, то 2128операций требуется для вскрытия алгоритма. (Эти операции могут быть сложными и длительными.) Так, если предполагается, что ваши вычислительные мощности способны выполнять миллион операций в секунду, и вы используете для решения задачи миллион параллельных процессоров, получение ключа займет у вас свыше 1019лет, что в миллиард раз превышает время существования вселенной. В то время как сложность вскрытия остается постоянной (пока какой-нибудь Криптоаналитик не придумает лучшего способа вскрытия), мощь компьютеров растет. За последние полвека вычислительные мощности феноменально выросли, и нет никаких причин подозревать, что эта тенденция не будет продолжена. Многие криптографические взломы пригодны для параллельных компьютеров: задача разбивается на миллиарды маленьких кусочков, решение которых не требует межпроцессорного взаимодействия. Объявление алгоритма безопасным просто потому, что его нелегко взломать, используя современную технику, в лучшем случае ненадежно. Хорошие криптосистемы проектируются устойчивыми к взлому с учетом развития вычислительных средств на много лет вперед.
Принциип Керкгоффса — правило разработки криптографических систем, согласно которому в засекреченном виде держится только определённый набор параметров алгоритма, называемый ключом, а остальные детали могут быть открыты без снижения стойкости алгоритма ниже допустимых значений. Другими словами, при оценке надёжности шифрования необходимо предполагать, что противник знает об используемой системе шифрования всё, кроме применяемых ключей.
Сущность принципа заключается в том, что чем меньше секретов содержит система, тем выше её безопасность. Так, если утрата любого из секретов приводит к разрушению системы, то система с меньшим числом секретов будет надёжней. Чем больше секретов содержит система, тем более она ненадёжна и потенциально уязвима. Чем меньше секретов в системе — тем выше её прочность.
Принцип Керкгоффса направлен на то, чтобы сделать безопасность алгоритмов и протоколов независимой от их секретности; открытость не должна влиять на безопасность.
Большинство широко используемых систем шифрования, в соответствии с принципом Керкгоффса, используют известные, не составляющие секрета криптографические алгоритмы. С другой стороны, шифры, используемые в правительственной и военной связи, как правило, засекречены; таким образом создаётся «дополнительный рубеж обороны».
Полный перебор (или метод 'грубой силы' от англ. brute-force) - метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от размерности пространства всех возможных решений задачи. В криптографии на сложности полного перебора основывается оценка криптостойкости шифров. В частности, шифр считается криптостойким, если не существует метода взлома, существенно более быстрого, чем полный перебор всех ключей.
Настройки атаки перебором состоят из двух частей.
Первая вкладка предназначена для задания диапазона перебираемых символов. Можно выбрать уже готовые заготовки или задать свои собственные. Чтобы задать свой диапазон символов, следует выставить опцию 'Пользовательский набор'. После этого, для формирования своего набора, станут доступны два поля ввода: первое - для ввода ASCII, второе - для ввода непечатных символов. Свой набор можно сохранить на диске.
Во второй вкладке необходимо задать минимальную и максимальную длину перебираемых паролей. Важно помнить, что для атаки на LM хэши, максимальная длина не должна превышать 7 символов. Можно также задать и стартовый пароль, с которого начнется перебор. Таблица ниже дает наглядное представление о сложности пароля и зависимости его от длины и набора символов. Подразумевается, что скорость перебора составляет 100 млн. паролей в секунду.
Совершенная секретность.
Предположим, что имеется конечное число возможных сообщений M 1,..., M n с априорными вероятностями P (M 1),..., P (M n) и что эти сообщения преобразуются в возможные криптограммы E 1,..., E m, так что
E = TiM.
После того как шифровальщик противника перехватил некоторую криптограмму E, он может вычислить, по крайней мере в принципе, апостериорные вероятности различных сообщений P E (M). Естественно определить совершенную секретность с помощью следующего условия: для всех E апостериорные вероятности равны априорным вероятностям независимо от величины этих последних. В этом случае перехват сообщения не дает шифровальщику противника никакой информации. Теперь он не может корректировать никакие свои действия в зависимости от информации, содержащейся в криптограмме, так как все вероятности, относящиеся к содержанию криптограммы, не изменяются. С другой стороны, если это условие равенства вероятностей не выполнено, то имеются такие случаи, в которых для определенного ключа и определенных выборов сообщений апостериорные вероятности противника отличаются от априорных. А это в свою очередь может повлиять на выбор противником своих действий и, таким образом, совершенной секретности не получится. Следовательно, приведенное определение неизбежным образом следует из нашего интуитивного представления о совершенной секретности.
Необходимое и достаточное условие для того, чтобы система была совершенно секретной, можно записать в следующем виде. По теореме Байеса
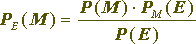 ,
,
где
P (M) – априорная вероятность сообщения M;
P M (E) – условная вероятность криптограммы E при условии, что выбрано сообщение M, т.е. сумма вероятностей всех тех ключей, которые переводят сообщение M в криптограмму E;
P (E) – вероятность получения криптограммы E;
P E (M) – апостериорная вероятность сообщения M при условии, что перехвачена криптограмма E.
Для совершенной секретности системы величины P E (M) и P (M) должны быть равны для всех E и M. Следовательно, должно быть выполнено одно из равенств: или P (M) = 0 [это решение должно быть отброшено, так как требуется, чтобы равенство осуществлялось при любых значениях P (M) ], или же
PM (E) = P (E)
для любых M и E. Наоборот, если P M (E) = P (E), то
PE (M) = P (M),
и система совершенно секретна. Таким образом, можно сформулировать следующее:
Теорема 6. Необходимое и достаточное условие для совершенной секретности состоит в том, что
PM (E) = P (E)
для всех M и E, т.е. P M (E) не должно зависеть от M.
Другими словами, полная вероятность всех ключей, переводящих сообщение Mi в данную криптограмму E, равна полной вероятности всех ключей, переводящих сообщение Mj в ту же самую криптограмму E для всех Mi, Mj и E.
Далее, должно существовать по крайней мере столько же криптограмм E, сколько и сообщений M, так как для фиксированного i отображение Ti дает взаимнооднозначное соответствие между всеми M и некоторыми из E. Для совершенно секретных систем для каждого из этих E и любого M P M (E) = P (E) 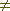 0. Следовательно, найдется по крайней мере один ключ, отображающий данное M в любое из E. Но все ключи, отображающие фиксированное M в различные E, должны быть различными, и поэтому число различных ключей не меньше числа сообщений M. Как показывает следующий пример, можно получить совершенную секретность, когда число сообщений точно равно числу ключей. Пусть Mi занумерованы числами от 1 до n, так же как и Ei, и пусть используются n ключей. Тогда
0. Следовательно, найдется по крайней мере один ключ, отображающий данное M в любое из E. Но все ключи, отображающие фиксированное M в различные E, должны быть различными, и поэтому число различных ключей не меньше числа сообщений M. Как показывает следующий пример, можно получить совершенную секретность, когда число сообщений точно равно числу ключей. Пусть Mi занумерованы числами от 1 до n, так же как и Ei, и пусть используются n ключей. Тогда
TiMj = Es,
где s = i + j (mod n). В этом случае оказывается справедливым равенство P E (M) = 1/ n = P (E) и система является совершенно секретной. Один пример такой системы показан на рис. 5, где
s = i + j – 1 (mod 5).

|
| Рис 5. Совершенная система. |
Совершенно секретные системы, в которых число криптограмм равно числу сообщений, а также числу ключей, характеризуются следующими двумя свойствами: 1) каждое M связывается с каждым E только одной линией; 2) все ключи равновероятны. Таким образом, матричное представление такой системы является "латинским квадратом".
В "Математической теории связи" показано, что количественно информацию удобно измерять с помощью энтропии. Если имеется некоторая совокупность возможностей с вероятностями p 1,..., p n, то энтропия дается выражением
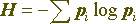 .
.
Секретная система включает в себя два статистических выбора: выбор сообщения и выбор ключа. Можно измерять количество информации, создаваемой при выборе сообщения, через H (M)
 ,
,
где суммирование выполняется по всем возможным сообщениям. Аналогично, неопределенность, связанная с выбором ключа, дается выражением
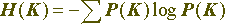 .
.
В совершенно секретных системах описанного выше типа количество информации в сообщении равно самое большее log n (эта величина достигается для равновероятных сообщений). Эта информация может быть скрыта полностью лишь тогда, когда неопределенность ключа не меньше log n. Это является первым примером общего принципа, который будет часто встречаться ниже: существует предел, которого нельзя превзойти при заданной неопределенности ключа – количество неопределенности, которое может быть введено в решение, не может быть больше, чем неопределенность ключа.
Положение несколько усложняется, если число сообщений бесконечно. Предположим, например, что сообщения порождаются соответствующим марковским процессом в виде бесконечной последовательности букв. Ясно, что никакой конечный ключ не даст совершенной секретности. Предположим тогда, что источник ключа порождает ключ аналогичным образом, т.е. как бесконечную последовательность символов.
Предположим далее, что для зашифрования и расшифрования сообщения длины LM требуется только определенная длина ключа LK. Пусть логарифм числа букв в алфавите сообщений будет RM, а такой же логарифм для ключа – RK. Тогда из рассуждений для конечного случая, очевидно, следует, что для совершенной секретности требуется, чтобы выполнялось неравенство
RMLM  RKLK.
RKLK.
Такой вид совершенной секретности реализован в системе Вернама.
Эти выводы делаются в предположении, что априорные вероятности сообщений неизвестны или произвольны. В этом случае ключ, требуемый для того, чтобы имела место совершенная секретность, зависит от полного числа возможных сообщений.
Можно было бы ожидать, что если в пространстве сообщений имеются фиксированные известные статистические связи, так что имеется определенная скорость создания сообщений R в смысле, принятом в "Математической теории связи", то необходимый объем ключа можно было бы снизить в среднем в R / R M раз, и это действительно верно. В самом деле, сообщение можно пропустить через преобразователь, который устраняет избыточность и уменьшает среднюю длину сообщения как раз во столько раз. Затем к результату можно применить шифр Вернама. Очевидно, что объем ключа, используемого на букву сообщения, статистически уменьшается на множитель R / R M, и в этом случае источник ключа и источник сообщений в точности согласован – один бит ключа полностью скрывает один бит информации сообщения. С помощью методов, использованных в "Математической теории связи", легко также показать, что это лучшее, чего можно достигнуть.
Совершенно секретные системы могут применяться и на практике, их можно использовать или в том случае, когда полной секретности придается чрезвычайно большое значение, например, для кодирования документов высших военных инстанций управления, или же в случаях, где число возможных сообщений мало. Так, беря крайний пример, когда имеются в виду только два сообщения – "да" или "нет", – можно, конечно, использовать совершенно секретную систему со следующей таблицей отображений:
| M | K | |
| A | B | |
| да | ||
| нет |
Недостатком совершенно секретных систем для случая корреспонденции большого объема является, конечно, то, что требуется посылать эквивалентный объем ключа.