ГЛАВА V
МЕТОДЫПЛАНИРОВАНИЯ
ЭКСТРЕМАЛЬНЫХ ЭКСПЕРИМЕНТОВ
Большое количество экспериментальных задач в химии и химической технологии формулируется как задачи экстремальные: определение оптимальных условий процесса, оптимального состава композиции и т. д. Благодаря оптимальному расположению точек в факторном пространстве и линейному преобразованию координат, удается преодолеть недостатки классического регрессионного анализа, в частности корреляцию между коэффициентами уравнения регрессии. Выбор плана эксперимента определяется постановкой задачи исследования и особенностями объекта. Процесс исследования обычно разбивается на отдельные этапы. Информация, полученная после каждого этапа, определяет дальнейшую стратегию эксперимента. Таким образом, возникает возможность оптимального управления экспериментом. Планирование эксперимента позволяет варьировать одновременно все факторы и получать количественные оценки основных эффектов и эффектов взаимодействия. Интересующие исследователя эффекты определяются с меньшей ошибкой, чем при традиционных методах исследования. В конечном счете, применение методов планирования значительно повышает эффективность эксперимента.
1. Полный факторный эксперимент. При планировании по схеме полного факторного эксперимента (ПФЭ) реализуются все возможные комбинации факторов на всех выбранных для исследования уровнях. Необходимое количество опытов N при ПФЭ определяется по формуле

где n – количество уровней; k – число факторов.
Если эксперименты проводятся только на двух уровнях, при двух значениях факторов и при этом в процессе эксперимента осуществляются все возможные комбинации из k факторов, то постановка опытов по такому плану называется полным факторным экспериментом типа  . Уровни факторов представляют собой границы исследуемой области по данному технологическому параметру. Например, изучается влияние на выход продукта
. Уровни факторов представляют собой границы исследуемой области по данному технологическому параметру. Например, изучается влияние на выход продукта  трех факторов: температуры
трех факторов: температуры  в диапазоне 100-200°C, давления
в диапазоне 100-200°C, давления 
 Па и времени пребывания
Па и времени пребывания  10-20 мин. Верхний уровень по температуре
10-20 мин. Верхний уровень по температуре 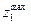 равен 200°C, нижний
равен 200°C, нижний 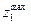 равен 100°С, Тогда для
равен 100°С, Тогда для  имеем
имеем
 ;
;  .
.
Вообще для любого фактора 
 ,
,  ; (V.1)
; (V.1)
 (V.2)
(V.2)
Точка с координатами  называется центром плана, иногда ее называют основным уровнем;
называется центром плана, иногда ее называют основным уровнем; 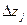 – интервал варьирования по оси
– интервал варьирования по оси  . От переменных
. От переменных  перейдем к новым –
перейдем к новым –  путем следующего линейного преобразования:
путем следующего линейного преобразования: 
 ,
,  ; (V.3)
; (V.3)
Для переменных  верхний уровень равен +1, нижний уровень –1, координаты центра плана равны нулю и совпадают с началом координат. В рассматриваемом примере
верхний уровень равен +1, нижний уровень –1, координаты центра плана равны нулю и совпадают с началом координат. В рассматриваемом примере  . Число возможных комбинаций
. Число возможных комбинаций  . План проведения экспериментов (матрица планирования) записывается в виде табл. 28.
. План проведения экспериментов (матрица планирования) записывается в виде табл. 28.
Представленный в табл. 28 план в безразмерном масштабе геометрически может быть интерпретирован в виде восьми вершин куба (рис. 28). Введем в ПФЭ  столбец так называемой фиктивной переменной
столбец так называемой фиктивной переменной  (табл. 29).
(табл. 29).
Приведенная в табл. 29 матрица планирования обладает следующими свойствами:
 (V.4)
(V.4)
где k – число независимых факторов; N – число опытов в матрице планирования.
Первое свойство (V.4) – равенство нулю скалярных произведений всех вектор-столбцов – называется свойством ортогональности матрицы планирования. Это свойство резко уменьшает трудности, связанные с расчетом коэффициентов уравнения регрессии, так как матрица коэффициентов нормальных уравнений  становится диагональной и ее диагональные элементы равны числу опытов в матрице планирования N.
становится диагональной и ее диагональные элементы равны числу опытов в матрице планирования N.

Таблица 28. Полный факторный эксперимент 
| Номер опыта | Факторы в натуральном масштабе | Факторы в безразмерном масштабе | |||||

| 
| 
| 
| 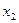
| 
| 
| |
| –1 +1 –1 +1 –1 +1 –1 +1 | –1 –1 +1 +1 –1 –1 +1 +1 | –1 –1 –1 –1 +1 +1 +1 +1 |
Таблица 29. Матрица планирования с фиктивной переменной
| Номер опыта | 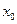
| 
| 
| 
| 
|
| +1 +1 +1 +1 +1 +1 +1 +1 | –1 +1 –1 +1 –1 +1 –1 +1 | –1 –1 +1 +1 –1 –1 +1 +1 | –1 –1 –1 –1 +1 +1 +1 +1 |




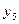


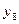
|
Коэффициенты уравнения регрессии по методу наименьших квадратов определяются следующим образом:

Матрица моментов  , соответствующая табл. 29, имеет вид
, соответствующая табл. 29, имеет вид
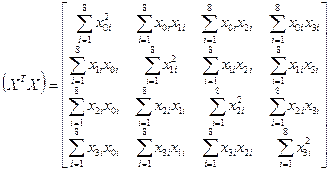
Учитывая свойства (V.4), получим 
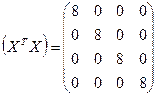 (V.5)
(V.5)
Матрица, обратная матрице моментов 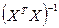 , получается равной
, получается равной
 (V.6)
(V.6)
и
 (V.7)
(V.7)
Таким образом,
 (V.8)
(V.8)
Следовательно, любой коэффициент уравнения регрессии  определяется скалярным произведением столбца y на соответствующий столбец
определяется скалярным произведением столбца y на соответствующий столбец  , делением на число опытов в матрице планирования N:
, делением на число опытов в матрице планирования N:
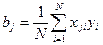 (V.9)
(V.9)
Пользуясь планом, представленным в табл. 28, сначала выясним коэффициенты линейного уравнения регрессии
 (V.10)
(V.10)
Например, для определения коэффициента 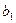 при
при  необходимо получить сумму произведений:
необходимо получить сумму произведений:





Аналогично получим  ;
;  ;
;  . Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия
. Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия
 (V.11)
(V.11)
то для определения коэффициентов  ,
,  ,
,  (эффектов парного взаимодействия) и
(эффектов парного взаимодействия) и  (эффекта тройного взаимодействия) необходимо расширить матрицу (табл. 29) следующим образом (табл. 30).
(эффекта тройного взаимодействия) необходимо расширить матрицу (табл. 29) следующим образом (табл. 30).
Таблица 30. Расширенная матрица планирования полного факторного
эксперимента 
| Номер опыта | 
| 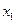
| 
| 
| 
| 
| 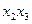
| 
| 
|
| +1 +1+1 +1+1 +1 +1 +1 | –1 +1–1 +1–1 +1 –1 +1 | –1 –1 +1 +1 –1 –1 +1 +1 | –1 –1 –1 –1 +1 +1 +1 +1 | +1 –1 –1 +1 +1 –1 –1 +1 | +1 –1 +1 –1 –1 +1 –1 +1 | +1 +1 –1 –1 –1 –1 +1 +1 | –1 +1 +1 –1 +1 –1 –1 +1 |
Эффекты взаимодействия определяются аналогично линейным эффектам. Так для определения коэффициента  необходимо:
необходимо:





Остальные коэффициенты определяются подобным образом:
 ,
,  ,
,  .
.
Если поставить дополнительно параллельные опыты, можно определить  проверить значимость коэффициентов регрессии и при наличии степеней свободы – адекватность уравнения.
проверить значимость коэффициентов регрессии и при наличии степеней свободы – адекватность уравнения.
В связи с тем, ковариационная матрица  для спланированного эксперимента – матрица диагональная
для спланированного эксперимента – матрица диагональная
 (V.12)
(V.12)
коэффициенты уравнения регрессии некоррелированы между собой. Значимость коэффициентов уравнения регрессии можно проверить для каждого коэффициента в отдельности по критерию Стьюдента. Исключение из уравнения регрессии (V.11) незначимого коэффициента не скажется на остальных коэффициентах. При этом выборочные коэффициенты  оказываются так называемыми несмешанными оценками для соответствующих теоретических коэффициентов
оказываются так называемыми несмешанными оценками для соответствующих теоретических коэффициентов  :
:
 (V.13)
(V.13)
т.е. значения коэффициентов уравнения регрессии характеризуют вклад соответствующего фактора в величину у. Диагональные элементы ковариационной матрицы равны между собой, поэтому все коэффициенты уравнений (V.10) и (V.11) определяются с одинаковой точностью:
 (V.14)
(V.14)
Например, в центре плана поставлено дополнительно три параллельных опыта и получены следующие значения y:
 ,
,  ,
,  .
.
 ;
;
 ;
;  ;
;

Оценим значимость коэффициентов по критерию Стьюдента:
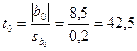 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Табличное значение критерия Стьюдента для уровня значимости  и числа степеней свободы
и числа степеней свободы 
 . Таким образом, коэффициенты
. Таким образом, коэффициенты  ,
,  ,
,  и
и  незначимы и их следует исключить из уравнения. После исключения незначимых коэффициентов уравнение регрессии имеет вид
незначимы и их следует исключить из уравнения. После исключения незначимых коэффициентов уравнение регрессии имеет вид
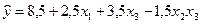
Проверим адекватность полученного уравнения по критерию Фишера:
 ;
;
 ;
;
 ;
;
l – число значимых коэффициентов в уравнении регрессии, равное 4. Тогда  . Табулированное значение критерия Фишера для
. Табулированное значение критерия Фишера для  ,
,  ,
,  ,
, 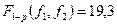 ,
,  .
.
Следовательно, полученное уравнение адекватно описывает эксперимент.
2. Дробные реплики. Если при получении уравнения можно ограничиться линейным приближением, то число опытов резко сокращается при использовании дробных реплик (см. гл. III, 4) от полного факторного эксперимента или дробного факторного эксперимента (ДФЭ). Чтобы дробная реплика представляла собой ортогональный план, в качестве реплики следует брать полный факторный эксперимент для меньшего числа факторов. Число опытов при этом должно быть больше (или равно) числа неизвестных коэффициентов в уравнении регрессии. Допустим, что нужно получить линейное приближение некоторого небольшого участка поверхности отклика при трех независимых факторах:

Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании для ПФЭ  (табл.31) использовать столбец
(табл.31) использовать столбец 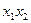 в качестве плана для
в качестве плана для 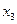 (табл. 32).
(табл. 32).
Таблица 31. Полный факторный эксперимент 
| Номер опыта | 
| 
| 
| 
|
| +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | +1 +1 –1 –1 |
Таблица 32. Полуреплика от ПФЭ 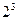
| Номер опыта | 
| 
| 
| 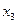
|
| +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | +1 +1 –1 –1 |
Такой сокращенный план – половина ПФЭ 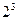 – называется полурепликой от ПФЭ
– называется полурепликой от ПФЭ 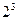 . Пользуясь таким планированием, можно оценить свободный член и три коэффициента уравнения регрессии при линейных членах.
. Пользуясь таким планированием, можно оценить свободный член и три коэффициента уравнения регрессии при линейных членах.
На практике обычно не удается априори постулировать равенство нулю эффектов взаимодействия, однако часто имеются основания полагать, что некоторые из них малы по сравнению с линейными эффектами. Если коэффициенты регрессии при парных произведениях не равны нулю, то полученные коэффициенты будут смешанными оценками для генеральных коэффициентов:
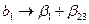 ,
,  ,
,  , (V.15)
, (V.15)
где  – математические ожидания для соответствующих коэффициентов.
– математические ожидания для соответствующих коэффициентов.
Эти генеральные коэффициенты не могут быть раздельно оценены по плану, включающему всего четыре опыта (табл. 32), так как при этом столбцы для линейных членов и парных произведений одинаковы.
Если, например, в дополнение к столбцам, приведенным в табл. 32, вычислить еще столбец для произведения  , то окажется, что элементы этого столбца в точности равны элементам столбца
, то окажется, что элементы этого столбца в точности равны элементам столбца 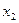 . Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Чтобы определить, какие генеральные коэффициенты смешаны, удобно пользоваться таким приемом: поставив
. Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Чтобы определить, какие генеральные коэффициенты смешаны, удобно пользоваться таким приемом: поставив 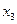 на место
на место 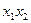 (табл. 32) получаем соотношение
(табл. 32) получаем соотношение
 (V.16)
(V.16)
называемое генерирующим соотношением. Умножим обе части генерирующего соотношения на 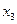 :
:
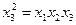
при этом слева получим единичный столбец:
 (V.17)
(V.17)
Произведение (V.17) называется определяющим контрастом, при помощи его удобно определить, в каких столбцах одинаковые элементы. Умножив по очереди определяющий контраст на  ,
,  ,
, 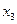 получим
получим
 ;
;  ;
;  . (V.18)
. (V.18)
Полученным соотношением (V.18) соответствует система смешанных оценок (V.15).
При использовании ДФЭ необходимо иметь четкое представление о так называемой решающей способности дробной реплики, т.е. определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих генеральных коэффициентов. Тогда в зависимости от поставленной задачи подбирается дробная реплика, при помощи которой можно извлечь максимальную информацию из эксперимента. Например, в задаче с четырьмя факторами  в качестве генерирующего соотношения можно взять
в качестве генерирующего соотношения можно взять
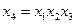 (V.19)
(V.19)
и любое из парных произведений факторов, например
 (V.20)
(V.20)
Матрица планирования с генерирующим соотношением (V.19) приведена в табл. 33.
Таблица 33. Полуреплика от ПФЭ  с генерирующим соотношением (V.19)
с генерирующим соотношением (V.19)
| Номер опыта | 
| 
| 
| 
| 
| Номер опыта | 
| 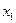
| 
| 
| 
|
| +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | +1 +1 +1 +1 | +1 +1 –1 –1 | +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | –1 –1 –1 –1 | –1 –1 +1 +1 |
Воспользовавшись определяющим контрастом  получим такую систему совместных оценок для коэффициентов уравнения регрессии:
получим такую систему совместных оценок для коэффициентов уравнения регрессии:
 (V.21)
(V.21)
В реальных задачах тройные взаимодействия бывают равными нулю значительно чаще, чем двойные. Если наибольший интерес представляют оценки для линейных эффектов, следует брать генерирующее соотношение  .
.
При регенерирующем соотношении (V.20) матрица планирования имеет вид (табл. 34).
Таблица 34. Полуреплика от ПФЭ  с генерирующим соотношением (V.20)
с генерирующим соотношением (V.20)
| Номер опыта | 
| 
| 
| 
| 
| Номер опыта | 
| 
| 
| 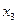
| 
|
| +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | +1 +1 +1 +1 | +1 +1 –1 –1 | +1 +1 +1 +1 | +1 –1 –1 +1 | +1 –1 +1 –1 | –1 –1 –1 –1 | –1 –1 +1 +1 |
Определяющий контраст выражается соотношением 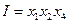 . Получается следующая система оценок:
. Получается следующая система оценок:
 (V.22)
(V.22)
Следовательно, дробную реплику с генерирующим соотношением  имеет смысл использовать, если наибольший интерес представляют коэффициенты
имеет смысл использовать, если наибольший интерес представляют коэффициенты 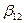 ,
,  и
и 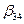 .
.
В полуреплике от ПФЭ  с генерирующим соотношением
с генерирующим соотношением  все линейные эффекты и эффекты парного взаимодействия смешаны только с эффектами тройного и более высокого порядков:
все линейные эффекты и эффекты парного взаимодействия смешаны только с эффектами тройного и более высокого порядков:
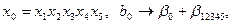






 (V.23)
(V.23)








Пренебрегая эффектами взаимодействия выше второго порядка, практически можно считать, что при 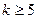 полуреплики от ПФЭ обеспечивают несмешанные оценки для линейных эффектов и эффектов парного взаимодействия. Используют в экспериментальной практике также и
полуреплики от ПФЭ обеспечивают несмешанные оценки для линейных эффектов и эффектов парного взаимодействия. Используют в экспериментальной практике также и  реплики,
реплики,  реплики и т.д. Дробную реплику, в которой p линейных эффектов приравнены к эффектам взаимодействия, обозначают
реплики и т.д. Дробную реплику, в которой p линейных эффектов приравнены к эффектам взаимодействия, обозначают  . Для четвертьреплики, например, в планировании для
. Для четвертьреплики, например, в планировании для  типа
типа  могут быть заданы генерирующие соотношения:
могут быть заданы генерирующие соотношения:
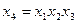 ,
,  .
.
Определяющими контрастами для этой реплики будут соотношения
 ,
,  . (V.24)
. (V.24)
Перемножив определяющие контрасты между собой, получим так называемый обобщающий определяющий контраст, который с учетом соотношений (V.24) полностью характеризует разрешающую способность реплик высокой степени дробности:
 . (V.25)
. (V.25)
При этом получается следующая система совместных оценок:
 (V.26)
(V.26)
Соответствующий план эксперимента приведен в табл. 35.
Таблица 35. Четвертьреплика от ПФЭ  с генерирующим
с генерирующим
Соотношением (V.24)
| Номер опыта | 
| 
| 
| 
| 
| Номер опыта | 
| 
| 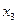
| 
| 
|
| +1 –1 –1 +1 | +1 –1 +1 –1 | +1 +1 +1 +1 | +1 +1 –1 –1 | +1 +1 –1 –1 | +1 –1 –1 +1 | +1 –1 +1 –1 | –1 –1 –1 –1 | –1 –1 +1 +1 | +1 +1 –1 –1 |
Разрешающая способность этой четвертьреплики невелика – все линейные эффекты смешаны с эффектами парного взаимодействия. ДФЭ можно дополнить до полного факторного эксперимента, реализовав недостающие дробные реплики. В рассматриваемом примере для остальных трех четвертьреплик генерирующие соотношения будут:
 (V.27)
(V.27)
При этом обобщающие определяющие контрасты имеют вид
 (V.28)
(V.28)
В результате реализации этих дополняющих четвертьреплик получаются несмешанные оценки для всех теоретических коэффициентов.
Число опытов в дробной реплике должно удовлетворять неравенству

(где k – число факторов) для получения несмешанных оценок линейных эффектов. Если число опытов N равно  – числу определяемых коэффициентов в линейном уравнении регрессии, дробная реплика представляет собой насыщенный линейный ортогональный план. В табл. 36 приведен насыщенный ортогональный план для
– числу определяемых коэффициентов в линейном уравнении регрессии, дробная реплика представляет собой насыщенный линейный ортогональный план. В табл. 36 приведен насыщенный ортогональный план для  , представляющий собой
, представляющий собой  ПФЭ
ПФЭ 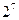 .
.
В табл. 36 факторы  ,
,  ,
,  и
и 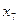 приравнены произведениям факторов:
приравнены произведениям факторов:

В связи с этим все линейные эффекты смешаны с эффектами взаимодействия.
Поскольку число опытов в насыщенных планах равно числу определяемых коэффициентов, число степеней свободы остаточной дисперсии равно нулю. Для проверки адекватности линейного уравнения, полученного по насыщенному плану, необходим дополнительный эксперимент.
Таблица 36. Линейный насыщенный план для 
| Номер опыта | 
| 
| 
| 
| 
| 
| 
| 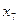
| Номер опыта | 
| 
| 
| 
| 
| 
| 
| 
|
| +1 +1 +1 +1 | –1 +1 –1 +1 | –1 +1 +1 –1 | –1 –1 –1 –1 | +1 +1 –1 –1 | +1 –1 +1 –1 | +1 –1 –1 +1 | –1 –1 +1 +1 | +1 +1 +1 +1 | –1 +1 –1 +1 | –1 +1 +1 –1 | +1 +1 +1 +1 | +1 +1 –1 –1 | –1 +1 –1 +1 | –1 +1 +1 –1 | +1 +1 –1 –1 |
Таким образом, оптимальные двухуровневые планы  и
и  имеют следующие преимущества: планы ортогональны, и поэтому все вычисления просты, все коэффициенты определяются независимо друг от друга; каждый коэффициент определяется по результатам всех N опытов. Эти планы обладают также свойством D-оптимальности:для данного числа опытов N они имеют минимальный определитель ковариационной матрицы
имеют следующие преимущества: планы ортогональны, и поэтому все вычисления просты, все коэффициенты определяются независимо друг от друга; каждый коэффициент определяется по результатам всех N опытов. Эти планы обладают также свойством D-оптимальности:для данного числа опытов N они имеют минимальный определитель ковариационной матрицы 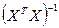 . Вследствие этого все коэффициенты регрессии определяются с одинаковой и минимальной дисперсией. Необходимо также отметить, что линейные планы
. Вследствие этого все коэффициенты регрессии определяются с одинаковой и минимальной дисперсией. Необходимо также отметить, что линейные планы  и
и  обладают свойством ротатабельности. Вследствие отсутствия корреляции между коэффициентами по закону сложения дисперсий для линейного уравнения при k факторах имеем:
обладают свойством ротатабельности. Вследствие отсутствия корреляции между коэффициентами по закону сложения дисперсий для линейного уравнения при k факторах имеем:
 . (V.29)
. (V.29)
Так как  , получим
, получим
 , (V.30)
, (V.30)
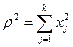 ,
,
 где
где  – квадрат радиуса сферы в k-мерном пространстве. Величину, обратную
– квадрат радиуса сферы в k-мерном пространстве. Величину, обратную  , можно принять за меру информации, содержащейся в уравнении регрессии. Согласно (V.30)количество информации убывает пропорционально квадрату радиуса сферы
, можно принять за меру информации, содержащейся в уравнении регрессии. Согласно (V.30)количество информации убывает пропорционально квадрату радиуса сферы  и одинаково для всех эквидистантных точек (рис. 29). Планирование, обладающее таким свойством, называют ротатабельным планированием.
и одинаково для всех эквидистантных точек (рис. 29). Планирование, обладающее таким свойством, называют ротатабельным планированием.
Приведем в общем виде схему дисперсионного и регрессионного анализов планированного эксперимента, когда каждый опыт в матрице планирования повторялся m раз (табл. 37).
Таблица 37. Матрица планирования и результаты измерений
| Номер опыта | 
| 
| 
| 
| 
| 
| 
|
| . . . N | +1 +1 +1 . . . +1 | +1 –1 +1 . . . –1 | –1 –1 +1 . . . +1 | …+1 …+1 …+1 . . . …–1 |

 .
.
.
.
.
.
.
.
.
.

|

 .
.
.
.
.
.
.
.
.
.

|

 .
.
.
.
.
.
.
.
.
.

|
В каждой строчке матрицы планирования определяется среднее значение измеряемой величины по m параллельным опытам:
 ,
,  . (V.31)
. (V.31)
и дисперсия
 ,
,  . (V.32)
. (V.32)
Проверяется однородность выборочных дисперсий по критерию Кохрена. Для этого составляется отношение максимальной дисперсии к сумме всех дисперсий:
 .
.
Полученное отношение сравнивается с табличным:  , где
, где  ;
;  ;
;  . Если
. Если  , дисперсии однородны.
, дисперсии однородны.
Тогда в качестве оценки для дисперсии воспроизводимости можно взять среднюю дисперсию
 . (V.33)
. (V.33)
с числом степеней свободы  .
.
Коэффициенты уравнения регрессии определяются по формуле
 . (V.34)
. (V.34)
Учитывая, что дисперсия  полученного по выборке объема m в m раз меньше дисперсии единичного измерения
полученного по выборке объема m в m раз меньше дисперсии единичного измерения
 . (V.35)
. (V.35)
в рассматриваемом примере (табл. 37) дисперсия коэффициентов  определяется следующим образом:
определяется следующим образом:
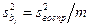 . (V.36)
. (V.36)
Значимость коэффициентов проверяется по критерию Стьюдента. В условиях нулевой гипотезы  , отношение абсолютной величины коэффициента уравнения регрессии к его ошибке имеет распределение Стьюдента. Для всех коэффициентов уравнения регрессии составляется t -отношение
, отношение абсолютной величины коэффициента уравнения регрессии к его ошибке имеет распределение Стьюдента. Для всех коэффициентов уравнения регрессии составляется t -отношение
 . (V.37)
. (V.37)
которое сравнивается с табличным  для уровня значимости
для уровня значимости  и числа степеней свободы
и числа степеней свободы  . Если
. Если  , то принимается гипотеза равен
, то принимается гипотеза равен