Флуктуации в идеальном газе

Средний квадрат флуктуации числа частиц обычного идеального газа, находящихся в некотором выделенном в газе относительно малом объеме, мы найдем, подставив в формулу , следующее выражение: . Это дает следующий простой результат; .

Относительная флуктуация числа частиц равна, следовательно, просто обратному квадратному корню из среднего числа частиц: .

Для того чтобы вычислить флуктуацию числа частиц в идеальном газе Бозе или Ферми, следует воспользоваться формулой , подставив в нее выражение для как функции от , , , получаемое интегрированием соответствующей функции распределения. Мы не станем выписывать здесь получающиеся таким способом довольно громоздкие выражения. Отметим лишь следующее обстоятельство. Можно видеть, что у бозе-гаэа при температурах 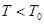давление не зависит от объема; другими словами, его сжимаемость обращается в бесконечность. Согласно формуле отсюда следовало бы, что флуктуации числа частиц тоже становятся бесконечными. Это означает, что при вычислении флуктуации в бозе-газе при низких температурах нельзя пренебрегать взаимодействием его частиц, сколь бы слабым оно ни было; учет этого взаимодействия, которое должно существовать во всяком реальном газе, привел бы к конечным флуктуациям.

Рассмотрим флуктуации в распределении частиц газа по различным квантовым состояниям. Введем снова в рассмотрение квантовые состояния частиц (включая в это понятие также и различные состояния их поступательного движения), и пусть - их числа заполнения.

Рассмотрим совокупность , частиц, находящихся в -м квантовом состоянии; ввиду полной статистической независимости этой системы частиц от остальных частиц газа можно применить к ней формулу :

.

В применении к ферми-газу надо подставить сюда . Произведя дифференцирование, найдем

(*)

Аналогичным образом найдем для бозе-газа

. (**)

Для больцмановского газа при подстановке получается, формула в которую переходят как (*), так и (**) при .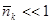

Просуммируем формулу (*) или (**) по группе из близких друг к другу состояний, содержащих всего частиц. В силу упомянутой уже статистической независимости флуктуации различных получим

, (***)

где — общее значение близких друг к другу , a .

Полученные формулы можно применить, в частности, к черному излучению, для чего надо положить в (**) . Рассмотрим совокупность квантовых состояний фотонов (в объеме ) с близкими значениями частот, лежащими в малом интервале ; число таких состояний равно . Общая энергия квантов в этом интервале частот есть . Умножив формулу (***) на и опуская индекс , получим следующее выражение для флуктуации энергии черного излучения в заданном интервале частот :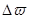

.

Корреляция флуктуации

Утверждение, что в однородном изотропном теле (газ или жидкость) все положения частиц в пространстве равновероятны, относится к каждой данной частице при условии, что все остальные частицы могут занимать произвольные положения. Это утверждение, конечно, не находится в противоречии с тем, что между взаимным расположением различных частиц должна существовать в силу их взаимодействия некоторая корреляция; последняя означает, что если рассматривать, скажем, одновременно две частицы, то при заданном положении первой частицы различные положения второй будут неравновероятными.

Для упрощения записи дальнейших формул мы ограничимся рассмотрением одноатомного вещества, у которого положение каждой частицы полностью определяется ее тремя координатами.

Обозначим посредством число частиц, находящихся (в данный момент времени) в элементе объема . В силу бесконечной малости объема в нем может находиться одновременно не более одной частицы; вероятность нахождения в нем сразу двух частиц есть бесконечно малая величина более высокого порядка. Поэтому среднее число частиц есть в то же время вероятность частице находиться в элементе .

Рассмотрим среднее значение

, (*)

где — значения плотности числа частиц в двух различных точках пространства, а посредством обозначено среднее значение плотности, одинаковое в силу однородности тела во всех, его точках (). Если бы между положениями различных частиц никакой корреляции не было, то мы имели бы и среднее значение (*) обратилось бы в нуль. Таким образом эта величина может служить мерой корреляции.

Обозначим посредством вероятность частице находиться в элементе объема при условии, что одна частица находится в элементе ; есть функция абсолютной величины относительного расстояния обоих элементов.

Поскольку, как уже было отмечено,. число есть 0 или 1, то очевидно, что среднее значение

или

В этом соотношении, справедливом при , нельзя, однако, перейти к пределу , так как при выводе не учтено, что если точки 1 и 2 совпадают, то частица, находящаяся в , тем самым находится и в . Легко видеть, что соотношение, учитывающее это обстоятельство, имеет вид

. (**)

Действительно, выделим некоторый малый объем и, умножив (**) на , проинтегрируем по этому объему. Член даст при этом малую величину второго порядка (пропорциональную ); член же с -функцией даст , т. е. величину первого порядка. Мы получим, следовательно,

как и должно быть, принимая во внимание, что с точностью, до величин первого порядка в малом объеме может находиться лишь 0 или 1 частица. Подставляя (**) в (*), найдем:

, (***)

где мы ввели функцию

, (****)

которую будем называть функцией корреляции. Ясно, что корреляция должна исчезать при неограниченном возрастании расстояния , т.е.

. (*****)

Выделим в рассматриваемом теле некоторый конечный объем и, умножив равенство (***) на , проинтегрируем по и . Имея в виду, что

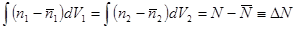
где — полное число частиц в объеме (так что ), найдем:

Переходя от интегрирования по и к интегрированию, скажем, по и по относительным координатам , (произведение дифференциалов которых обозначим ) и имея в виду, что зависит только от , получим окончательно следующее выражение для интеграла от функции корреляции:

. (******)

Таким образом, интеграл от функции корреляции по некоторому объему связан со средним квадратом флуктуации полного числа частиц в этом объеме. Воспользовавшись для последнего термодинамической формулой , можно выразить этот интеграл через термодинамические величины:

(*******)

В обычном (классическом) идеальном газе получается:

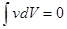
как и должно быть. Ясно, что в идеальном газе, рассматриваемом с точки зрения классической механики, никакой корреляции между положениями различных частиц вообще нет, поскольку частицы идеального газа предполагаются невзаимодействующими друг с другом.

Напротив, в жидкости (при температурах, не близких к критической точке) первый член в выражении (*******) мал по сравнению с единицей в силу малой сжимаемости жидкости.. В этом случае можем написать:

Это значение интеграла от функции корреляции в некотором смысле соответствует взаимной непроницаемости частиц жидкости, рассматриваемых как плотно упакованные твердые шарики.

Далее, умножим равенство (***) с обеих сторон на и снова проинтегрируем по Мы получим:

или окончательно:

. (********)

Это соотношение определяет компоненты Фурье функции корреляции через средние квадраты компонент Фурье плотности 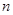.