Флуктуации в критической точке

В критической точке сжимаемость вещества 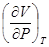и теплоемкость 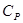становятся бесконечными. Вместе с ними обращаются формально в бесконечность выражения 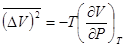и 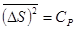для флуктуации объема (т. е. плотности) и энтропии; флуктуации же температуры и давления остаются конечными. Это значит, что в критической точке флуктуации плотности и энтропии становятся аномально большими, и для их вычисления необходимо произвести разложение 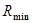в формуле 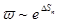до членов более высокого порядка малости, чем обращающиеся в данном случае в нуль члены второго порядка. Рассмотрим подробно флуктуации плотности вблизи критической точки.

Поскольку флуктуации плотности и температуры статистически независимы, то при рассмотрении флуктуации плотности температуру можно считать постоянной. Постоянным является по определению также и полный объем тела в целом. В таких условиях минимальная работа 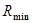равна изменению 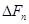полной свободной энергии тела при флуктуации, так что вероятность последней можно написать в виде

(*)

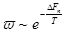Представив полную свободную энергию тела в виде интеграла

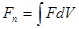
взятого по всему объему тела, причем 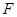обозначает свободную энергию, отнесенную к единице объема. Пусть 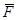есть среднее значение 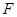, постоянное вдоль тела. В результате флуктуации 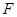становится вместе с плотностью величиной, меняющейся от точки к точке тела, причем

(**)

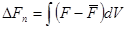Обозначим плотность числа частиц посредством 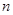(ее среднее значение 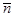) и разложим 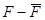в ряд по степеням 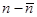при постоянной температуре.

Первый член разложения пропорционален 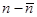и при интегрировании по объему обращается в нуль в силу постоянства полного числа частиц в теле: 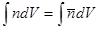.. Член второго порядка имеет вид 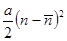, где положительный коэффициент 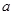обращается в самой критической точке в нуль, а вблизи нее является малой величиной. Коэффициент в члене третьего порядка тоже мал вблизи критической точки (в критической точке обращаются в нуль не только 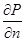, но и 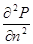), такчто надо было бы учесть член четвертого порядка. В действительности, однако, в разложении 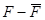содержатся большие члены другого характера.

Дело в том, что до сих пор мы всегда рассматривали термодинамические величины однородных тел. В неоднородном же теле разложение 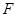может содержать не только различные степени самой плотности, но и ее производных различного порядка по координатам. Благодаря изотропии тела первые производные могут войти в разложение плотности лишь в виде скалярной комбинации 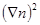а вторые — в виде комбинации 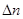( 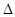— здесь оператор Лапласа). Интеграл по объему от члена вида 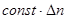преобразуется в интеграл по поверхности тела, представляющий собой не интересующий нас поверхностный эффект. Интеграл же от члена вида 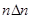преобразуется в интеграл от 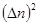. Таким образом, не ограничивая общности, мы можем положить:

(***)

где 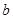— положительная постоянная (при 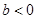свободная энергия не могла бы иметь минимума, соответствующего 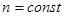); эта постоянная отнюдь не должна обращаться в нуль в критической точке и потому вблизи последней — не мала.

Вычисление средних флуктуации плотности в определенных малых участках тела представляет сравнительно мало интереса; ввиду наличия в (***) члена с производными от плотности эти флуктуации будут зависеть не только от объема, но и от формы участка. Значительно больший интерес имеет вопрос о флуктуациях компонент Фурье плотности вблизи критической точки.

Разложим 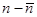в ряд Фурье в объеме тела, представив его в виде

(****)

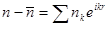причем компоненты вектора 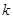пробегают как положительные, так и отрицательные значения, а коэффициенты

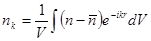
связаны соотношениями

,

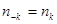следующими из вещественности 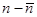. Подставив (****) в (***) и проинтегрировав по объему, получим:

(*****)

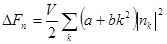Каждый из членов этой суммы зависит только от одного из ; поэтому флуктуации различных статистически независимы. Каждый квадрат 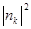входит в сумму (*****) дважды (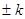), так что распределение вероятностей его флуктуации дается выражением

.

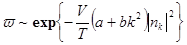Имея в виду, что 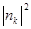есть сумма квадратов двух независимых величин ( комплексно), найдем отсюда для искомого среднего квадрата флуктуации:

(******)

Следует подчеркнуть, что эти формулы применимы лишь при не слишком больших значениях волнового вектора 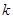; при больших 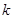уже нельзя ограничиваться в разложении (***) членами, содержащими только низшие производные от плотности по координатам.

Полученный результат дает возможность вычислить функцию корреляции 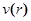вблизи критической точки. Согласно общей формуле 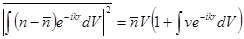имеем:

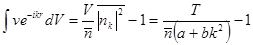
Первый член справа, вообще говоря, велик по сравнению с единицей, поскольку предполагаются малыми как , так и 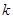. Поэтому можно написать:

(*******)

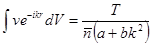Отсюда путем обратного преобразования Фурье найдем:

(********)

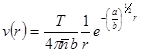Коэффициент перед 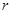в показателе мал в силу малости . В самой критической точке 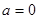, так что экспоненциально убывающий множитель исчезает вовсе:

(*********)

Таким образом, вблизи критической точки корреляция между положениями различных частиц в веществе весьма медленно убывает с расстоянием, т. е. становится гораздо более сильной, чем в обычных условиях, когда она практически исчезает уже на расстояниях порядка величины межмолекулярных.