Распределение Гаусса
Физические величины, характеризующие равновесное макроскопическое тело, практически всегда с очень большой точностью равны своим средним значениям. Однако, как ни малы отклонения от средних значений они все же происходят (величины, как говорят, флуктуируют), и возникает вопрос о нахождении распределения вероятностей этих отклонений.
Рассмотрим какую-либо замкнутую систему, и пусть  есть некоторая физическая величина, характеризующая систему в целом или какую-либо ее часть (в первом случае это, конечно, не должна быть величина, остающаяся для замкнутой системы строго постоянной, как, например, ее энергия).
есть некоторая физическая величина, характеризующая систему в целом или какую-либо ее часть (в первом случае это, конечно, не должна быть величина, остающаяся для замкнутой системы строго постоянной, как, например, ее энергия).
Ели рассматривать формальным образом энтропию системы как функцию от точных значений энергий подсистем, то функция  будет давать распределение вероятностей для этих энергий. Однако, в этих рассуждениях не используются какие-либо специфические свойства энергии. Поэтому такие же рассуждения приведут к результату, что вероятность величине
будет давать распределение вероятностей для этих энергий. Однако, в этих рассуждениях не используются какие-либо специфические свойства энергии. Поэтому такие же рассуждения приведут к результату, что вероятность величине  иметь значение в интервале между
иметь значение в интервале между  и
и  пропорциональна
пропорциональна 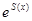 , где
, где  —энтропия, формально рассматриваемая как функция точного значения
—энтропия, формально рассматриваемая как функция точного значения  . Обозначив вероятность посредством
. Обозначив вероятность посредством  имеем
имеем
 (*)
(*)
Прежде чем приступить к исследованию этой формулы, остановимся на вопросе о пределах ее применимости. Все рассуждения, которые привели к формуле (*), неявно подразумевают классичность поведения величины  . Поэтому надо найти условие, допускающее пренебрежение квантовыми эффектами.
. Поэтому надо найти условие, допускающее пренебрежение квантовыми эффектами.
Как известно из квантовой механики, между квантовыми неопределенностями энергии и какой-либо величины  имеет место соотношение
имеет место соотношение  , где
, где  — классическая скорость изменения величины
— классическая скорость изменения величины  .
.
Пусть 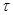 — время, характеризующее скорость изменения интересующей нас величины
— время, характеризующее скорость изменения интересующей нас величины  , которая имеет неравновесное значение; тогда
, которая имеет неравновесное значение; тогда  , так что
, так что  .
.
Ясно, что говорить об определенном значении величины  можно лишь при условии малости ее квантовой, неопределенности:
можно лишь при условии малости ее квантовой, неопределенности:  , откуда
, откуда 
Таким образом, квантовая неопределенность энергии должна быть велика по сравнению с  . Энтропия же системы будет при этом иметь неопределенность
. Энтропия же системы будет при этом иметь неопределенность  .
.
Для того чтобы формула (*) имела реальный смысл, необходимо, очевидно, чтобы неточность энтропии была мала по сравнению с единицей:
 (**)
(**)
Это и есть искомое условие. При слишком низких температурах или при слишком быстром изменении величины  (слишком малом
(слишком малом 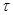 ) флуктуации нельзя рассматривать термодинамически, и на первый план выступают чисто квантовые флуктуации.
) флуктуации нельзя рассматривать термодинамически, и на первый план выступают чисто квантовые флуктуации.
Вернемся к формуле (*). Энтропия  имеет максимум при
имеет максимум при  . Поэтому
. Поэтому  ,
,  .
.
Величина  при флуктуациях очень мала. Разлагая
при флуктуациях очень мала. Разлагая  в ряд по степеням
в ряд по степеням  и ограничиваясь членом второго порядка, получим
и ограничиваясь членом второго порядка, получим  где
где  —положительная постоянная. Подставляя в (*), получим распределение вероятностей в виде
—положительная постоянная. Подставляя в (*), получим распределение вероятностей в виде 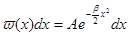
Нормировочная постоянная  определяется условием
определяется условием  хотя выражение для
хотя выражение для  относится к малым
относится к малым  , но ввиду быстрого убывания подынтегральной функции с увеличением
, но ввиду быстрого убывания подынтегральной функции с увеличением  область интегрирования можно распространить на все значения от
область интегрирования можно распространить на все значения от  до
до  . Произведя интегрирование, получим
. Произведя интегрирование, получим  .
.
Таким образом, распределение вероятностей для различных значений флуктуации  определяется формулой
определяется формулой
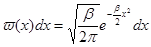 . (***)
. (***)
Распределение такого вида называется распределением Гаусса. Оно имеет максимум при 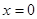 и быстро спадает с увеличением
и быстро спадает с увеличением  симметрично в обе стороны.
симметрично в обе стороны.
Средний квадрат флуктуации равен
 .
.
Поэтому распределение Гаусса можно написать в виде  .
.
Как и следовало,  имеет тем более острый максимум, чем меньше
имеет тем более острый максимум, чем меньше 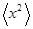 .
.
Отметим, что по известному 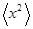 можно найти аналогичную величину для любой функции
можно найти аналогичную величину для любой функции  . В виду малости
. В виду малости  имеем
имеем  .
.
Флуктуации основных термодинамических величин
Для таких величин, как энергия, объем и т. п., имеющих наряду с термодинамическим также и чисто механический смысл, понятие флуктуации само собой очевидно. Оно нуждается, однако, в уточнении для таких величин, как энтропия и температура, определение которых неизбежно связано с рассмотрением тела в течение конечных интервалов времени. Пусть, например,  есть равновесная энтропия тела как функция его (средних) энергии и объема. Мы будем понимать под флуктуацией энтропии изменение функции
есть равновесная энтропия тела как функция его (средних) энергии и объема. Мы будем понимать под флуктуацией энтропии изменение функции  , рассматриваемой формально как функция от точных (флуктуирующих) значений энергии и объема.
, рассматриваемой формально как функция от точных (флуктуирующих) значений энергии и объема.
Вероятность  флуктуации пропорциональна
флуктуации пропорциональна  , где
, где  — полная энтропия замкнутой системы, т. е. всего тела в целом. С тем же успехом можно написать, что
— полная энтропия замкнутой системы, т. е. всего тела в целом. С тем же успехом можно написать, что  пропорциональна
пропорциональна  , где
, где  — изменение энтропии при флуктуации. Согласно формуле
— изменение энтропии при флуктуации. Согласно формуле  имеем:
имеем:  где
где 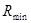 — минимальная работа, необходимая для того, чтобы обратимым образом произвести заданное изменение термодинамических величин данной малой части тела (по отношению к которой остальные части тела играют роль среды). Таким образом,
— минимальная работа, необходимая для того, чтобы обратимым образом произвести заданное изменение термодинамических величин данной малой части тела (по отношению к которой остальные части тела играют роль среды). Таким образом,  . Подставим сюда для
. Подставим сюда для 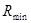 выражение
выражение  где
где  ,
, 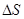 ,
,  - изменения энергии, энтропии и объема данной малой части тела при флуктуации, а
- изменения энергии, энтропии и объема данной малой части тела при флуктуации, а 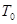 и
и  — температура и давление «среды», т.е. равновесные (средние) значения температуры и давления тела.
— температура и давление «среды», т.е. равновесные (средние) значения температуры и давления тела.
Таким образом, имеем
 (*)
(*)
Заметим, что в таком виде эта формула применима к любым флуктуациям — как небольшим, так и значительным; под значительными здесь подразумеваются такие флуктуации, при которых, например,  сравнимо с энергией самой малой части тела, но, конечно, по-прежнему мало по сравнению с энергией тела в целом. В применении к малым флуктуациям (какими они, вообще говоря, являются) формула (*) дает следующее. Разлагая
сравнимо с энергией самой малой части тела, но, конечно, по-прежнему мало по сравнению с энергией тела в целом. В применении к малым флуктуациям (какими они, вообще говоря, являются) формула (*) дает следующее. Разлагая  в ряд, получим
в ряд, получим
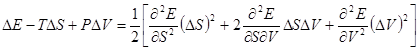 .
.
Это выражение можно написать в виде
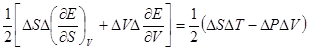 .
.
Таким образом, получаем вероятность (*) флуктуации в виде
 . (**)
. (**)
Из этой общей формулы можно найти флуктуации различных термодинамических величин. Выберем сначала в качестве независимых переменных  и
и  . Тогда
. Тогда
 ,
,

Подставляя эти выражения в показатель формулы (**), найдем, что члены с  сокращаются, и остается
сокращаются, и остается
 . (***)
. (***)
Это выражение распадается на два множителя, зависящих только от 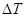 или
или  . Другими словами, флуктуации температуры и объема статистически независимы, а потому
. Другими словами, флуктуации температуры и объема статистически независимы, а потому  .
.
Сравнивая поочередно каждый из двух множителей, на которые распадается (***), с общей формулой  распределения Гаусса, найдем следующие выражения для средних квадратов флуктуации температуры и объема:
распределения Гаусса, найдем следующие выражения для средних квадратов флуктуации температуры и объема:
 , (/*/)
, (/*/)
 . (****)
. (****)
Положительность этих величин обеспечивается термодинамическими неравенствами  и
и  .
.
Выберем теперь в качестве независимых переменных в (**)  и
и  . Тогда
. Тогда
 ,
,
 .
.
Но согласно формуле  имеем
имеем  , и поэтому
, и поэтому  . Подставляя
. Подставляя 
 и
и 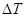 в (**), находим
в (**), находим
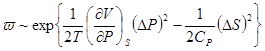 .
.
Как и (***) это выражение распадается на множители, зависящие соответственно от 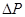 и
и  . Другими словами, флуктуации энтропии и давления статистически независимы, и потому
. Другими словами, флуктуации энтропии и давления статистически независимы, и потому 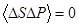 .
.
Для средних квадратов флуктуации энтропии и давления находим  ,
, 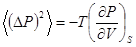 .
.
Из полученных формул видно, что средние квадраты флуктуации аддитивных термодинамических величин — обьема и энтропии—пропорциональны размерам (объему) тех частей тела, к которым они относятся. Соответственно средняя квадратичная флуктуация этих величин пропорциональна квадратному корню из объема, а относительная флуктуация — обратно пропорциональна этому корню. Для таких же величин, как температура и давление, обратно пропорциональны корню из объема уже сами их средние квадратичные флуктуации.
Формула (****) определяет флуктуацию объема некоторой части тела, содержащей определенное число  частиц. Деля обе стороны равенства на
частиц. Деля обе стороны равенства на  , находим флуктуацию объема, приходящегося на одну частицу:
, находим флуктуацию объема, приходящегося на одну частицу:
 (*****)
(*****)
Эта величина, очевидно, не может зависеть от того, рассматриваем ли мы флуктуацию в постоянном объеме или для постоянного числа частиц. Поэтому из последней формулы можно найти флуктуацию числа частиц, находящихся в определенном выделенном в теле объеме. Поскольку при этом  есть заданная величина, то надо положить
есть заданная величина, то надо положить 
.Подставляя это в (*****), находим 
Для некоторых вычислений удобно представить эту формулу в ином виде. Замечая, что производная  подразумевается взятой при постоянном
подразумевается взятой при постоянном  , пишем
, пишем  .
.
Но число частиц  как функция от
как функция от  ,
,  ,
,  в силу соображений аддитивности должно иметь вид
в силу соображений аддитивности должно иметь вид  ; другими словами,
; другими словами,  есть функция только от
есть функция только от  и
и  , и потому безразлично, производится ли дифференцирование
, и потому безразлично, производится ли дифференцирование  при постоянном
при постоянном  или
или  , так что можно написать:
, так что можно написать:

(мы воспользовались равенством  ). Таким образом, получаем следующую формулу для флуктуации числа частиц.
). Таким образом, получаем следующую формулу для флуктуации числа частиц.

Наряду с рассмотренными термодинамическими величинами, тело характеризуется также импульсом  своего макроскопического движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т.е.
своего макроскопического движения относительно среды. В состоянии равновесия никакого макроскопического движения нет, т.е.  . Движение, однако, может появиться в результате флуктуации; определим вероятность такой флуктуации. Минимальная работа
. Движение, однако, может появиться в результате флуктуации; определим вероятность такой флуктуации. Минимальная работа 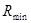 в этом случае равна просто кинетической энергии тела
в этом случае равна просто кинетической энергии тела 
где  — его масса,
— его масса,  — скорость макроскопического движения. Таким образом, имеем для искомой вероятности
— скорость макроскопического движения. Таким образом, имеем для искомой вероятности  .
.
Отметим, что флуктуации скорости статистически независимы от флуктуации других термодинамических величин. Средний квадрат флуктуации каждой из декартовых компонент скорости равен  он обратно пропорционален массе тела.
он обратно пропорционален массе тела.
Из выведенных формул видно, что средние квадраты флуктуации таких величин, как энергия, объем, давление, скорость, обращаются при абсолютном нуле в нуль (пропорционально первой степени температуры). Это является общим свойством всех термодинамических величин, имеющих также и чисто механический смысл, но, вообще говоря, не относится к таким чисто термодинамическим величинам, как энтропия и температура.
Формула (/*/) для флуктуации температуры может быть истолкована еще и с другой точки зрения. Как мы знаем, понятие температуры может быть введено через посредство распределения Гиббса; при этом температура рассматривается как параметр, определяющий это распределение. В применении к изолированному телу распределение Гиббса полностью описывает его статистические свойства с той лишь неточностью, что оно дает весьма малые, но все же отличные от нуля флуктуации полной энергии тела, которых в действительности не должно быть. Напротив, если считать энергию величиной заданной, то нельзя приписывать телу вполне определенную температуру, и надо считать, что последняя испытывает флуктуации, определяющиеся формулой (/*/), в которой  будет теплоемкостью тела в целом. Эта величина, очевидно, характеризует точность, с которой может быть дано определение температуры изолированного тела.
будет теплоемкостью тела в целом. Эта величина, очевидно, характеризует точность, с которой может быть дано определение температуры изолированного тела.