3. Актуализация ЗУН, необходимых для творческого применения знаний.
4. Формирование новых понятий и способов действий
5. Обобщение и систематизация знаний и способов деятельности
6. Усвоение образца комплексного применения ЗУН
7. Применение знаний умений и навыков в новых условиях
8. Подведение итогов урока
Ход урока:
1. Организация начала урока. Проверка присутствующих,
2. Постановка проблемы урока. Постановка целей и задач урока.
3. Актуализация ЗУН, необходимых для творческого применения знаний.
Проиллюстрируем фрагмент урока. Чтобы заитересовать учащихся даются исторические сведения об интеграле (Слайд 2).
Формирование новых понятий и способов действий.
Определение криволинейной трапеции. Площадь криволинейной трапеции. Если на [а;b] ([а;b]?Ох) функция у=f(х) – непрерывная, не меняет знак (график не пересекает ось абсцисс), тогда фигура, ограниченная графиком функции f, отрезком [а;b] и прямыми х = а, х = b, называется криволинейной трапецией (слайд 8).
Если f - непрерывная и неотрицательная на отрезке [а;b] функция, а F – её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [а;b], т.е.
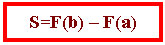
Введение понятия "интеграл".
Рассмотрим другой подход к задаче вычисления площади криволинейной трапеции. Для простоты будем считать функцию f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.
Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x0 = а<x1 < x2 < … <xn-1 < xn = b и пусть
,
|
|
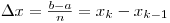где k = 1, 2,..., n — 1, n. На каждом из отрезков [xk-1; xk] как на основании построим прямоугольник высотой F(xk-1). Площадь этого прямоугольника равна:
а сумма площадей всех таких прямоугольников равна:
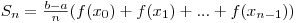
В силу непрерывности функции f объединение построенных прямоугольников при большом n, т. е. при малом Δx, "почти совпадает" с интересующей нас криволинейной трапецией. Поэтому возникает предположение, что Sn≈S при больших n. (Коротко говорят: "Sn стремится к S при n, стремящемся к бесконечности"— и пишут: Sn→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) Sn при n→∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до b и обозначают 
, т. е.
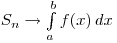при n→∞
(читается: "Интеграл от а до b эф от икс дэ икс"). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак 
называют знаком интеграла. Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой
Полный конспект урока см. приложение 1.
В теме "Применение интегралов" мы изучили площадей криволинейных трапеций с помощью интегралов. В процессе проведения опытно-экспериментальной работы нами был разработан план урока для 11 класса на тему: "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью MS Excel" с применением интерактивных досок и информационных технологий (урок 7). Приведем фрагмент урока по теме 7 (см. приложение 1).
|
|
Тема урока: Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. Вычисление определенного интеграла с помощью программ MS Excel.
Цель: Обеспечить закрепление понятия интеграл, способы его вычисления, применение интеграла для вычисления площадей.
Задачи:
Обучающая: сформировать навыки планирования ответа, умение считать и писать в быстром темпе, навыки самоконтроля
Развивающая: развивать познавательную потребность учащихся.
Воспитательная: воспитывать умение организовать свою деятельность, формирование ценностной ориентации, мировоззрения.
Содержание урока: Данная тема рассчитана на два часа и состоит из двух частей: часть 1 – "Вычисление интегралов и площадей криволинейных трапеций с помощью интегралов. В процессе изучения данной темы учащиеся узнают о физическом приложении интеграла.
План урока: