2. Обобщение и систематизация знаний и способов деятельности
3. Подведение итогов урока
Ход урока
1. Организация начала урока.
Проверка домашнего задания с места (фронтально).
Сегодня на уроке мы должны обобщить все знания и умения по теме "Первообразная и интеграл" с целью подготовки к контрольной работе. Начнём повторение мы с устной работы, затем проведём групповую работу, которая откроет нам некоторые исторические факты. Вспомним вычисление площадей фигур, а также повторим, где используют интеграл в физике. В заключении урока проведём самостоятельную работу по перфокартам.
Устная работа (фронтально).
1)На экране спроецирована таблица для устного счёта. Для функций, указанных в таблице, составить хотя бы одну первообразную. (Таблица в презентации).
2) Устное повторение теоретического материала (фронтально):
- Дайте определение первообразной.
- Как читается основное свойство первообразной?
- Какие правила нахождения первообразной существуют?
- Что называется неопределённым интегралом?
- Что называется криволинейной трапецией?
- Как выглядит формула Ньютона – Лейбница?
- В чём состоит геометрический смысл определенного интеграла?
- В чём состоит физический смысл определенного интеграла?
3)Верно ли? На слайде для каждой функции f(x) записана первообразная F(x), но в записи первообразной есть ошибка. Найдите ошибку и прокомментируйте.
f(x)=(8x-5)2, F(x)=(8x-5)3/3+C
Ответ: не хватает перед первообразной множителя 1/8так, как функция f(x) сложная.
f(x)=sin(5+4x), F(x)= -1/5cos(5+4x)+C
Ответ: перед первообразной должен быть множитель1/4, а не 1/5так, как коэффициент к=4.

Ответ: не хватает перед первообразной множителя 2.
2. Обобщение и систематизация знаний и способов деятельности
1а) Групповая работа над темой. На экране через проектор с компьютера проецируются портреты математиков: 1 - Лейбница, 2 - И. Бернулли, 3 - Ферма, 4 – Я. Бернулли, 5 - Ньютона. Класс делится на пять групп. Каждая группа получает карточку со своим заданием: найти значение постоянной С. На этой же карточке дана историческая справка о вкладе конкретного учёного в развитие теории интегрального исчисления. Вычислив значение С, каждая группа связывает это число с номером портрета математика. Представитель от группы зачитывает историческую справку для других. (Портреты в презентации, задания для групп в приложениях 1 и 2).
1б) Продолжим групповую работу. Установить соответствие.
На экране три функции f,g,h и три графика первообразных для данных функций. Для каждой функции записать первообразную и найти график этой первообразной. Решают все на месте в тетрадях также группами, затем озвучивают результаты.
1. f(x)=sinx, 2. g(x)=cosx, 3. h(x)=cos2x



Решение:
F(x)= -cosx+C, G(x)=sinx+C, H(x)=0,5 sin2x+C
2) Устно. Первообразная тесно связана с интегралом. Мы с вами вспоминали формулу Ньютона – Лейбница. Вы знаете, что определённый интеграл используют для вычисления площадей плоских фигур, и в первую очередь для вычисления площади криволинейной трапеции.
Посмотрим на экран и выясним являются ли фигуры криволинейными трапециями.




Физкультминутка
3) Работа у доски. Три ученика выходят к доске и получают карточки с заданием вычислить площадь фигуры. Остальные учащиеся на местах решают две задачи на нахождение площади фигур, затем правильность решения проверяется с помощью проектора.
Задание классу.
Учебник №360(г), №364(г).
Задание 1 ученику - №365(в),
Задание 2 ученику - №365(г),
Задание 3 ученику - №361(б).
4) Работа у доски.
Определённый интеграл используют и в других дисциплинах. Например, на уроках физики с помощью определённого интеграла можно вычислить работу переменной силы, массу, центр масс, электрический заряд, перемещение и количество теплоты.
Задача 1.Сила упругости пружины, растянутой на 6 см, равна 4,2 Н. Какую работу надо произвести, чтобы растянуть пружину на 6см?
Решение:F=kx;
4,2=k*0,06;
k=420:6;
k=70, F=70x
5) Контролирующая самостоятельная работа по перфокартам.
В каждом варианте 6 заданий. К каждому заданию 4 варианта ответов, только один из них правильный. У каждого ученика на парте лежит контрольный талон. Решив задание в тетради, уч – ся выбирает номер верного ответа и зачёркивает его в контрольном талоне. После выполнения всех 6 заданий в каждом контрольном талоне будет зачёркнуто 6 чисел. Ученики сдают талоны учителю, который при помощи шаблона с прорезями быстро проверяет работы, накладывая шаблон на талон.
Контрольный талон
| Фамилия, имя Класс вариант | ||||
Шаблон для проверки
1 вариант
| Х | ||||
| Х | X | |||
| Х | X | |||
| X |
2 вариант
| X | ||||
| Х | X | |||
| X | ||||
| X | ||||
| X |
Знак "Х" означает места прорезей в шаблоне.
Оценка результатов:
6 крестиков верных – "5";
5 крестиков верных – "4";
4 крестика верных – "3";
3 и меньше – "2".
6) Индивидуальное проблемное задание для тех, кто быстро справился с самостоятельной раньше других:
При каком положительном значении параметра а площадь фигуры, ограниченной линиями y= 1/x2, y=0, x=1, x=a равна 7/8?
3. Подведение итогов урока
Подводится итог урока. Цель нашего урока была обобщить знания по теме "Первообразная. Интеграл." Давайте посмотрим как мы работали. На экран с помощью проектора выводится таблица. Поднимите руку, если вы
- знаете таблицу первообразных;
- умеете пользоваться таблицей для нахождения первообразной сложной функции;
- легко находите площадь криволинейной трапеции;
- умеете применять интеграл для решения физических задач.
Те, кто поднял руку на все вопросы, готовы к выполнению контрольной работы. Остальным надо подготовиться лучше. Выставляются оценки за работу на уроке. Задаётся домашнее задание.
Для развития познавательной потребности нами предлагается во внеклассной форме работы использование различных видов уроков для развития познавательной потребности учащихся. Мы, например, использовали урок-КВН (см. приложение 1).
Урок КВН по теме "Интеграл"
Цель: обобщение изученного материала по теме, формирование умений применять математические задания к решению практических задач.
Задачи:
Развивающие: развитие познавательной потребности, творческих способностей.
Воспитательные: воспитание интереса к предмету, воспитание чувства коллективизма и взаимовыручки.
КВН проводится интерактивно с помощью сайта школы.
На экране ЭВМ написано:
| I команда | II команда |
(Ниже ведётся запись полученных очков).
Правила игры.
Класс разбивается на две команды.
Выбираются капитаны команд.
Капитаны назначают консультантов.
Для участия во всех видах работы ученики вызываются к доске капитанами команд.
Ход урока.
1 этап. Разминка – ведется на бумажном носителе.
На экране ЭВМ написаны задания.
II этап. Блиц – турнир – проводится с помощью ЭВМ (желательно применение проектора).
III этап. Домашнее задание.
К доске приглашаются по 1 ученику от каждой команды.
1. С помощью интеграла вывести формулу объёма конуса.
2. С помощью интеграла вывести формулу объёма шара.
IV этап. Конкурс капитанов.
V этап. Конкурс болельщиков – задания проектируются на доску с помощью проектора, а также дублируются на сайте школы.
VI этап. Конкурс эрудитов - задания проектируются на доску с помощью проектора, а также дублируются на сайте школы
1. Вычислите:
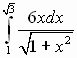
2. Вычислите:
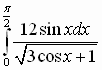
Решение 1.
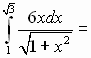
Пусть 
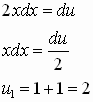
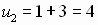

Решение 2.
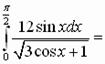
Пусть 


VII этап. Конкурс консультантов. (дополнительный) – проводится при помощи Mathcad.
VIII этап. Подведение итогов.
Выигравшая команда объявляется победительницей, а многие учащиеся получают оценки.
Итак, применение информационных технологий в преподавании темы "Интегралы":
1. Содействует воспитанию аккуратности, организованности, дисциплины;
2. Формирует умения работать коллективно, в группе, паре, самостоятельно;
3. Прививает интерес к предмету посредством применения современных информационных технологий;
4. Способствует развитию интеллектуальных качеств личности школьника: самостоятельность, гибкость, способности видеть проблему, обобщать, переключаться с одного вида работы на другой;
5. Развивает эмоции учащихся, создавая эмоциональные ситуации удивления, сопереживания;
6. Развивает познавательный интерес, создавая игровые ситуации.