Ценность месторождения облицовочного камня определяется не только декоративностью и долговечностью камня, но и блочностью массива, обусловленной его природной трещиноватостью. В свою очередь, от блочности массива и принятой технологии добычных работ зависит коэффициент выхода товарных блоков из извлеченного полезного ископаемого. Величина этого коэффициента, предопределенная характером взаимного пересечения в массиве плоскостей трещин и плоскостей забоя, оказывает влияние на себестоимость добычи блоков, производительность труда, объем запасов, производственную мощность карьера и срок его существования.
Сейчас уже очевидно, что время поиска месторождений с высоким коэффициентом выхода блоков миновало и необходимо изыскивать способы интенсификации добычи блоков на имеющихся месторождениях и, прежде всего, за счет применения рациональной технологии и эффективных технических средств. Поэтому приоритетность должны получать такие технологические решения, посредством которых можно обеспечить наибольщую полноту использования добытого камня.
Для повышения выхода товарных блоков в процессе подготовки камня к выемке применяют двухстадийную схему отработки месторождения. При этом размеры отделяемого монолита камня выбирают такими, чтобы свести к минимуму влияние объема монолита и природной трещиноватости массива на выход товарных блоков.
Процесс добычи блоков по двухстадийной схеме наиболее эффективно реализуется с помощью одних канатных пил либо канатных пил в комбинации с баровыми машинами. Таким образом, научное обоснование рациональных геометрических параметров отделяемого от массива породы монолита с целью повышения выхода конечной продукции при наименьших трудозатратах является основным направлением совершенствования технологии добычи блоков по двухстадийной схеме.
Тезис акад. А.М. Терпигорева о том, что горное дело есть концентрированная экономика, для карьеров облицовочного камня является не менее значимым, чем для карьеров других твердых полезных ископаемых. В данном случае извлекаемая ценность единицы объема полезного ископаемого значительно выше, чем даже у самых богатых руд цветных металлов. Вследствие этого экономическая оценка различных технологических схем добычи облицовочного камня с учетом особенностей применяемых технических средств является обоснованной и общепризнанной как отечественными, так и зарубежными исследователями.
Значения рациональных параметров монолита можно определить, минимизируя затраты на выполнение добычных работ, согласно их стадийности. В качестве оптимизационного критерия примем условие, при котором удельные затраты по подготовке монолита к выемке путем прорезания направленных щелей в массиве должны быть минимальными [44], т.е.
 р./м3 ® min, (4.14)
р./м3 ® min, (4.14)
где Cs – удельные затраты, связанные с резанием камня при отделении монолита от массива, р./м2;
Sm – удельная площадь обнажения монолита в массиве, м-1;
Кв – коэффициент выхода товарных блоков из объема монолита.
Длина монолита L, характеризуемая длиной пропила, не влияет на энергосиловые показатели канатных пил, но в совокупности с высотой пропила устанавливает необходимую протяженность канатно-алмазного контура. Ширину монолита В отражает технологический параметр, определяющий заходку канатной пилы на новый рез. В связи с трудоемкостью выемки монолита из массива величина его объема является фактором, ограничивающим максимально предельные размеры монолита. Высота монолита Н, как высота добычного уступа и пропила, связана с протяженностью контактного взаимодействия инструмента с породой. И поэтому влияет на энергосиловые показатели, производительность процесса резания, удельный расход алмазного инструмента и, таким образом, на экономику добычных работ.
Из изложенного очевидно, что высота уступа (пропила) должна являться оптимальной величиной, и поэтому минимизировать удельные затраты согласно (4.14) необходимо по данному технологическому параметру.
Для определения оптимальной высоты уступа (монолита) из условия минимума удельных эксплуатационных затрат, связанных с подготовкой к выемке блочного камня из массива, 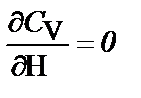 имеем следующее дифференциальное уравнение:
имеем следующее дифференциальное уравнение:
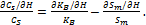 (4.15)
(4.15)
Для решения полученного оптимизационного условия необходимо, чтобы его составляющими были функциональные связи, достоверно и достаточно отражающие технико-экономические показатели процесса резания камня канатными пилами и структурно-геологическую оценку месторождения. Обоснование и расчет входящих в оптимизационное уравнение (4.15) показателей и параметров приведем в следующей последовательности.
Удельная площадь обнажения монолита в массиве Sm определяется по общеизвестной формуле
 (4.16)
(4.16)
где H, L и B – высота, длина и ширина монолита, м.
Зависимость удельной площади обнажения Sm от высоты монолита Hпредставлена на рис.4.1. Анализ полученных зависимостей показывает, что с увеличением высоты монолита с 1 до 8 м удельная площадь обнажения монолита снижается на 51, 55 и 58% при поперечных размерах монолита соответственно 1,8  6 м; 2,2
6 м; 2,2  8 м; 2,5
8 м; 2,5  10 м. Представленные расчеты свидетельствуют о значительном сокращении объемов распиловочных работ, связанных с отделением монолитов от массива, при переходе на высокоуступную технологию.
10 м. Представленные расчеты свидетельствуют о значительном сокращении объемов распиловочных работ, связанных с отделением монолитов от массива, при переходе на высокоуступную технологию.

Высота монолита Н, м
Рис.4.1. График зависимости удельной площади обнажения Sm
от высоты монолита при ширине и длине монолита соответственно:
1 – 1,8 и 6 м; 2 – 2,2 и 8 м; 3 – 2,5 и 10 м
Примем закономерность изменения коэффициента выхода товарных блоков от высоты добычного уступа в виде степенной зависимости
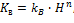 (4.17)
(4.17)
где коэффициент пропорциональности kв и показатель степени n определяются значением длины L и ширины В монолита, величиной минимального объема используемых в дальнейшей переработке блоков, а также интенсивностью природных трещин массива.
Величина показателя степени n в формуле (4.17) определялась по значениям коэффициентов КВ1, Кв2 выхода товарных блоков при высотах уступов H1 и H2, м в диапазоне H =1-12 м с использованием соотношения
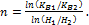 (4.18)
(4.18)
Значения коэффициентов КВ1, КВ2 зависят от трещиноватости разрабатываемого месторождения, минимального размера товарного блока, размеров отделяемых монолитов (рис.4.2), направления фронта горных работ и т.д.

Рис.4.2. График зависимости коэффициента выхода товарных блоков
от высоты монолита (H) при различных ширине (B) и длине (L) его:
1 B  L=1,8
L=1,8  6 м; 2 - B
6 м; 2 - B  L=2,2
L=2,2  8 м; 3 - b
8 м; 3 - b  L=2,5
L=2,5  10 м
10 м
Параметры степенной аппроксимации коэффициента выхода товарных блоков, рассчитанные для условий Коелгинского месторождения мрамора, имеют следующие усредненные значения:
kв = 1,5 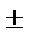 0,1; n=0,4 - 0,6.
0,1; n=0,4 - 0,6.
Зависимости коэффициента выхода товарных блоков от высоты при различной длине и ширине монолита представлены на рис.4.2. (при минимальном объеме товарного блока 1 м3), исходные данные для которого приведены в табл.3.6.
Анализ зависимостей свидетельствует о возрастании коэффициента выхода товарных блоков при увеличении размеров монолита. Увеличение выхода товарных блоков показывает преимущества высокоуступной технологии и подтверждает необходимость определения оптимального значения высоты монолита из условия минимума удельных затрат.
Удельные затраты на резание камня определяются согласно зависимости (4.13), где скорость подачи инструмента на забой согласно формул (4.4 и 4.12) находится из следующего соотношения:
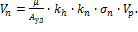 (4.19)
(4.19)
Критерии 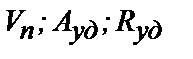 представляют функции от режимов резания, физико-механических свойств породы и алмазного инструмента. Поэтому экономико-математическая модель поверхностного разрушения горной породы алмазно-абразивным инструментом (4.13) дает возможность произвести оптимизацию процесса распиловки как по геометрии забоя, так и по режимным параметрам в зависимости от прочностных свойств породы и конструктивных особенностей инструмента.
представляют функции от режимов резания, физико-механических свойств породы и алмазного инструмента. Поэтому экономико-математическая модель поверхностного разрушения горной породы алмазно-абразивным инструментом (4.13) дает возможность произвести оптимизацию процесса распиловки как по геометрии забоя, так и по режимным параметрам в зависимости от прочностных свойств породы и конструктивных особенностей инструмента.
При этом оптимизация (4.13) с использованием (4.19) становится возможной, если определена аналитическая связь между шириной и высотой пропила. Такая связь выявляется из усталостно-прочностного расчета несущего каната при условии соответствия периода его работоспособности, времени полного износа алмазонесущего слоя режущих элементов, которая в первом приближении имеет прямолинейную зависимость [39]:
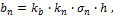 (4.20)
(4.20)
где kb - коэффициент, зависящий от усталостно-прочностных свойств несущего каната, конструктивных особенностей гибкого режущего инструмента, а также абразивной износостойкости алмазонесущего слоя режущих элементов
(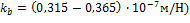 при условии
при условии 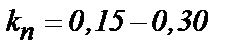 ;
;
kп – коэффициент прерывистости инструмента (отношение длины режущей поверхности к общей длине алмазно-канатного контура).
Минимальной себестоимости пиления единицы поверхности камня соответствует условие
 (4.21)
(4.21)
тогда оптимальная величина высоты (глубины) пропила с учетом соотношений (4.22) и (4.23) определяется из следующего выражения:
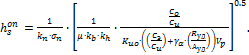 (4.22)
(4.22)
Существенное влияние на технико-экономические показатели процесса распиловки и, таким образом, на оптимальные значения  оказывает силовой режим резания, в связи с чем величина контактного давления также должна определяться из условия минимальных удельных затрат СS —>min.
оказывает силовой режим резания, в связи с чем величина контактного давления также должна определяться из условия минимальных удельных затрат СS —>min.
На обоснованность определения оптимального значения  указывает тот факт, что затраты на алмазорежущий инструмент составляют более половины всех удельных затрат при добыче камня данным оборудованием рис.4.3.
указывает тот факт, что затраты на алмазорежущий инструмент составляют более половины всех удельных затрат при добыче камня данным оборудованием рис.4.3.
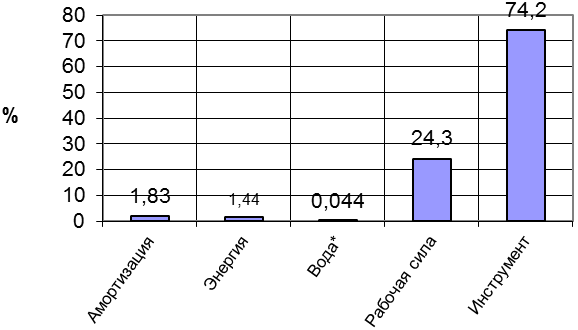
Рис.4.3. Доли статей затрат алмазно-канатной распиловки
Из приведенных на рис.4.3. данных следует, что статья затрат, связанная с расходом алмазного инструмента, является определяющей, поэтому с целью упрощения дальнейших расчетов учитываем только изменение расхода алмазного инструмента от силового режима.
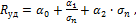 (4.23)
(4.23)
где 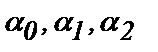 - коэффициенты, характеризующие абразивную износостойкость инструмента.
- коэффициенты, характеризующие абразивную износостойкость инструмента.
Оптимальный силовой режим 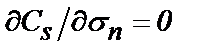 для случая линейной зависимости (4.20) сводится к условию
для случая линейной зависимости (4.20) сводится к условию 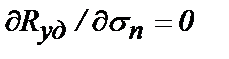 , решение которого и дает оптимальное давление [40]
, решение которого и дает оптимальное давление [40]
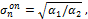 (4.24)
(4.24)
Из результатов экспериментальных исследований, выполненных в работе [5] и приведенных в табл. 4.1, очевидно, что в расчетах по определению 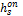 необходимо применить
необходимо применить 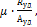 соответствующее
соответствующее 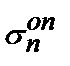 , т.е. условию
, т.е. условию 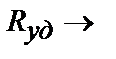 min (табл.4.2).
min (табл.4.2).
Для численного расчета оптимизационной модели (4.22) анализировались опубликованные отечественные и зарубежные результаты по расходу алмазного инструмента и энергии в зависимости от силового режима резания, по оценке статей эксплуатационных затрат при распиловке горных пород различной прочности, по организации работ по подготовке к выемке из массива и последующей разделке объемов камня канатными пилами. Анализ стоимостных параметров показывает, что определяющими поэлементными затратами являются расходы на амортизацию оборудования и заработную плату рабочих.
Поэтому отношение параметров Со/Си в наибольшей степени оказывает влияние на конечные результаты исследуемой модели. Причем Со/Си существенно отличается при сравнении отечественных (0,5-1,0 карат/ч) и зарубежных (2,0-2,5 карат/ч) данных. Это обусловлено различиями уровней заработной платы и цены алмазного инструмента. Затраты, связанные с количеством потребляемой энергии, невелики по сравнению со стоимостью алмазного инструмента и в расчетах их можно не учитывать, т.е. принять Сэ/Си = 0.
Таблица 4.1
Показатели относительного расхода алмазного инструмента,
полученные по данным работы [5]
| Удельное контактное давление | Месторождение, прочность | |||||
Коелгинское,
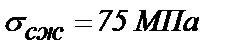
| Иджеванское,
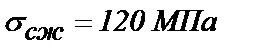
| Рускеальское,
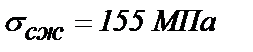
| ||||
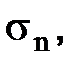 МПа МПа
|  , кар/дж , кар/дж
| 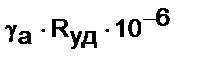 ,
кар/мм3 ,
кар/мм3
|  , кар/дж , кар/дж
| 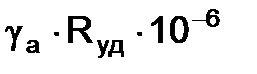 ,
кар/мм3 ,
кар/мм3
|  , кар/дж , кар/дж
| 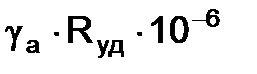 ,
кар/мм3 ,
кар/мм3
|
| 0,037 | 0,85 | 0,0205 | 1,95 | 0,0628 | 2,35 | 0,0943 |
| 0,092 | 0,82 | 0,0175 | 1,72 | 0,0568 | 1,95 | 0,795 |
| 0,148 | 0,56 | 0,0123 | 1,68 | 0,557 | 1,92 | 0,0692 |
| 0,185 | 0,46 | 0,0099 | 1,52 | 0,456 | 1,65 | 0,0599 |
| 0,222 | 0,4 | 0,0088 | 1,42 | 0,466 | 1,46 | 0,0565 |
| 0,259 | 0,5 | 0,116 | 1,62 | 0,492 | 1,69 | 0,0614 |
| 0,296 | 0,57 | 0,0139 | 1,83 | 0,0565 | 1,88 | 0,0663 |
| 0,333 | 0,76 | 0,0181 | 1,89 | 0,0579 | 2,15 | 0,0748 |
Таблица 4.2
| Месторождение, прочность | Коэффициенты абразивной стойкости алмазного инструмента | |||
| a0*10-5 | a1*10-5 МПа | a2*10-5 1/МПа |  МПа МПа
| |
Коелгинское 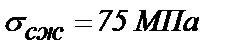
| -1,520 | 0,169 | 5,200 | 0,18 |
Иджеванское 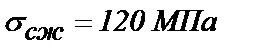
| 6,280 | -0,262 | 9,300 | 0,17 |
Рускеальское
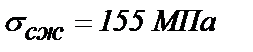
| -1,460 | 0,376 | 10,500 | 0,19 |
Для применяемого алмазно-канатного инструмента на горных породах типа мраморов с пределом прочности sсж = 50-70 МПа, отношением С0/Си= 0,5-1,0 кар./ч, при Кио = 0,5-0,75, sn = 0,25-0,3 МПа и Vр = 30-40 м/с, соответствующим Rуд®min, минимальные затраты по обнажению единицы поверхности достигаются при высоте пропила 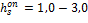 , м (рис. 4.4).
, м (рис. 4.4).
Для Коелгинского месторождения мрамора по формуле (4.22) получено соответствующее этой оценке значение 
 2 м.
2 м.
Как следует из рис.4.4, в качестве переменного управляемого параметра при определении оптимального диапазона высоты пропила должен рассматриваться лишь коэффициент прерывистости режущей поверхности.
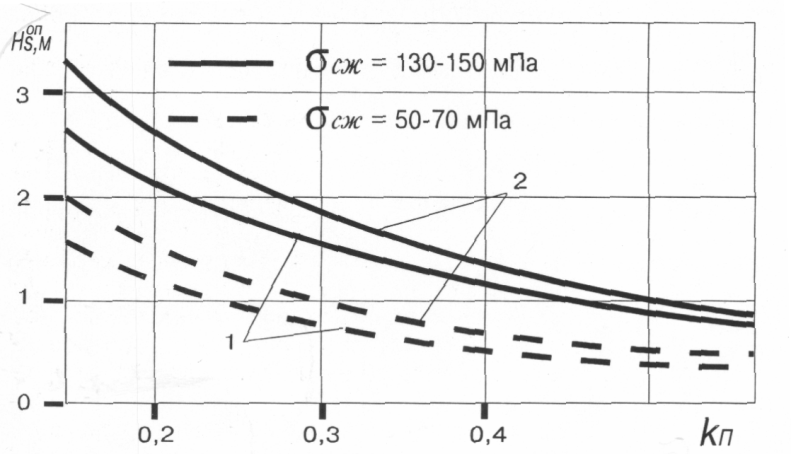
Рис. 4.4. Зависимость оптимальной высоты пропила  от величины коэффициента
от величины коэффициента  для мрамора различной прочности
для мрамора различной прочности
Закономерности экономического соотношения между высотой пропила и коэффициентом  такова, что наименьшему значению последнего соответствует предельная оптимальная величина высоты пропила, то есть между параметрами
такова, что наименьшему значению последнего соответствует предельная оптимальная величина высоты пропила, то есть между параметрами 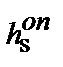 и
и  существует обратно пропорциональная связь.
существует обратно пропорциональная связь.
Коэффициент прерывистости режущей поверхности  является основной характеристикой конструкции инструмента, так как показывает долю длины контура, приходящуюся на алмазорежущие элементы. Данный коэффициент имеет максимальное и минимальное значение. Минимальная величина
является основной характеристикой конструкции инструмента, так как показывает долю длины контура, приходящуюся на алмазорежущие элементы. Данный коэффициент имеет максимальное и минимальное значение. Минимальная величина  соответствует такому положению алмазорежущих втулок вдоль каната, когда при его изгибе на распиливаемом блоке камня отсутствует контактное давление дистанционных элементов на дно пропила. По линии резания происходит вторичный изгиб каната между двумя соседними алмазорежущими втулками, в результате чего канат и смонтированные на этих участках дистанционные элементы (пружины) получают радиальное смещение до контакта с породой. Величина смещения зависит от длины пролета расположения алмазорежущих втулок и радиуса изгиба каната на распиливаемом блоке камня. Поэтому, задаваясь радиусом линии резания, определяемом высотой блока камня, можно рассчитать минимальное значение коэффициента
соответствует такому положению алмазорежущих втулок вдоль каната, когда при его изгибе на распиливаемом блоке камня отсутствует контактное давление дистанционных элементов на дно пропила. По линии резания происходит вторичный изгиб каната между двумя соседними алмазорежущими втулками, в результате чего канат и смонтированные на этих участках дистанционные элементы (пружины) получают радиальное смещение до контакта с породой. Величина смещения зависит от длины пролета расположения алмазорежущих втулок и радиуса изгиба каната на распиливаемом блоке камня. Поэтому, задаваясь радиусом линии резания, определяемом высотой блока камня, можно рассчитать минимальное значение коэффициента  , которое не приводит к нежелательному контакту дистанционных элементов с породой. В противном случае наблюдается снижение нормального давления алмазорежущих втулок на распиливаемую породу, а также повышенный износ дистанционных пружин и их последующая преждевременная поломка. Существенное влияние на долговечность дистанционных элементов оказывают условия и продолжительность работы инструмента в нестационарных режимах. Именно в периоды запиловки и допиливания реза, когда радиус кривизны забоя минимален, создаются самые неблагоприятные условия эксплуатации как для контура в целом, так и для его составляющих элементов.
, которое не приводит к нежелательному контакту дистанционных элементов с породой. В противном случае наблюдается снижение нормального давления алмазорежущих втулок на распиливаемую породу, а также повышенный износ дистанционных пружин и их последующая преждевременная поломка. Существенное влияние на долговечность дистанционных элементов оказывают условия и продолжительность работы инструмента в нестационарных режимах. Именно в периоды запиловки и допиливания реза, когда радиус кривизны забоя минимален, создаются самые неблагоприятные условия эксплуатации как для контура в целом, так и для его составляющих элементов.
Расчеты и практика показывают, что применение гибкого режущего контура с коэффициентом  меньше 0,15 нецелесообразно из-за низкой стойкости дистанционных элементов.
меньше 0,15 нецелесообразно из-за низкой стойкости дистанционных элементов.
С другой стороны, максимальное значение коэффициента kп ограничивает конструктивное условие, при котором жесткость гибкого режущего инструмента существенно повышается с уменьшением расстояния между алмазорежущими втулками, что в итоге ведет к снижению усталостной работоспособности каната. При этом необходимо отметить влияние величины промежутков между алмазорежущими втулками на эффективность выноса шлама из зоны пропила. Участки контура между втулками являются сборниками транспортируемого шлама, и поэтому их суммарная длина в доль пропила должна быть увязана с количеством диспергированного материала породы. На основании конструктивных соображений, а также с учетом вышесказанного, максимальная величина коэффициента прерывистости режущей поверхности инструмента может быть рекомендована в пределах 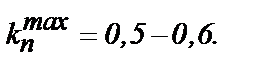 Определив таким образом реальный интервал варьирования коэффициента kп, мы устанавливаем и экономически обоснованные пределы изменения высоты пропила, в рамках которых достигаются наименьшие удельные затраты, связанные непосредственно с производством пропила.
Определив таким образом реальный интервал варьирования коэффициента kп, мы устанавливаем и экономически обоснованные пределы изменения высоты пропила, в рамках которых достигаются наименьшие удельные затраты, связанные непосредственно с производством пропила.
Проведенный анализ и расчет соответствующих показателей и параметров дает возможность путем дифференцирования выражений (4.13), (4.16), (4.17) согласно (4.15) получить искомое уравнение для определения оптимальной высоты уступа (монолита):
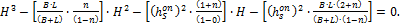 (4.25)
(4.25)
Как видим влияние естественной трещиноватости массива на оптимальное значение высоты уступа проявляется через показатель степени n, отражающий форму связи (4.17) между коэффициентом выхода товарных блоков и высотой монолита при некоторых заданных величинах его длины и ширины.
Зависимости оптимальных значений высоты монолита, рассчитанные по формуле (4.25) с учетом вышеприведенных составляющих, для монолитов различной длины и ширины, в условиях Коелгинского месторождения приведены на рис.4.5.
Полученные зависимости позволяют определять рациональное сочетание высоты уступа и заданных, технически и технологически обоснованных величин длины и ширины монолита для условий исследуемого месторождения. При этом ширина ограничивается параметрами оборудования, на котором распиливаются товарные блоки в камнеобрабатывающем цехе, длина - максимальной технологически возможной и безопасной площадью пропила. Далее из рационально сочетающихся размеров монолитов определяются оптимальные по условию минимума удельных затрат.

Рис.4.5. График зависимости оптимальных высот уступа
от длины и ширины монолита
Определение удельных затрат на добычу Сv для монолитов разных размеров по разработанной методике рис.4.6 свидетельствует о наличии зоны минимума удельных затрат и позволяет установить оптимальную высоту монолита. Для условий Коелгинского месторождения оптимальная высота монолита находится в пределах 6-8 м (см. рис. 4.6).
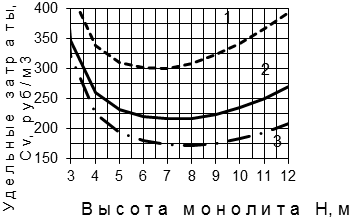
Рис. 4.6. График зависимости удельных затрат Сv
от высоты монолитов с шириной и длиной соответственно:
1 - 1,8 и 6 м; 2 - 2,2 и 8 м; 3 - 2,5 и 10 м
Установлено, что со снижением объема монолита оптимальное значение минимума удельных затрат повышается. Так, при уменьшении объема монолита на 34 и 70% удельные затраты Сv возрастают соответственно на 25,7 и 71,4%, а интервал оптимальных значений высоты монолита смещается в сторону ее уменьшения.
Степенное уравнение третьего порядка (4.25) является полным, поэтому решение в явном виде записать не удается, что затрудняет его аналитический анализ без составления специальной программы для компьютерного решения. Общий вид уравнения (4.25) можно изменить за счет упрощения постановки задачи, а именно, учитывать только те поверхности направленного обнажения монолита в массиве, которые связаны с высотой уступа, т.е. S=L ·H+B ·H, тогда поперечная площадь монолита S=L ·B не будет влиять на конечное решение. Задача в такой постановке была решена [43] и обоснована для комбинированной технологии добычи с применением баровых машин на горизонтальной подрезке монолита от массива. В этом случае поперечная площадь монолита не входит в состав удельной площади обнажения, производимой канатной пилой, что равносильно условию S=L ·B=0, подставив которое в уравнение (4.25) получим упрощенный вариант оптимизационной задачи.
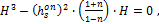 (4.26)
(4.26)
Решение (4.26) дает следующее оптимальное соотношение:
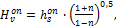 (4.27)
(4.27)
Для случая, когда n ® о (ΚВ®1), имеем равенство 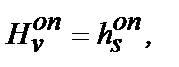 которое характеризует высокоблочный массив, практически не нарушенный природными трещинами. С другой стороны, такое положение характерно для разделочно-пассировочных работ, т.е. для второй стадии процесса добычи блоков облицовочного камня.
которое характеризует высокоблочный массив, практически не нарушенный природными трещинами. С другой стороны, такое положение характерно для разделочно-пассировочных работ, т.е. для второй стадии процесса добычи блоков облицовочного камня.
Таким образом, оптимизация технологических параметров по данной методике осуществляется в две стадии. На первой стадии производится экономическая оценка критериев процесса распиловки – производительности, удельной работы, удельного расхода инструмента; на второй стадии оцениваются удельные затраты по подготовке монолитов к выемке из массива породы с учетом влияния природной трещиноватости и геометрических параметров отделяемых объемов камня.
4.3. Влияние геометрических параметров