Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет - УПИ»
ФИЗИЧЕСКАЯ ХИМИЯ
Конспект лекций по курсу «Физическая химия»
для самостоятельной работы студентов дневной формы обучения
химико-технологического факультета и
факультета строительного материаловедения
Екатеринбург 2006
УДК 541.1
Составители:
Т.П.Больщикова, Л.А.Брусницына, Н.К.Булатов, А.Б.Лундин, Ю.Н.Макурин, В.Ф.Марков, Л.Н.Маскаева, Е.И.Степановских, А.А.Урицкая
Научный редактор доц., канд. хим. наук Степановских Е.И.
Физическая химия: конспект лекций / Т.П.Больщикова, Л.А.Брусницына, Н.К.Булатов, А.Б.Лундин, Ю.Н.Макурин, В.Ф.Марков, Л.Н.Маскаева, Е.И.Степановских, А.А.Урицкая. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 83 с.
Конспект лекций по физической химии составлен на основе различных вариантов лекций, читаемых преподавателями одной из старейших кафедр института − кафедры физической и коллоидной химии УГТУ-УПИ. В данной работе представлена часть лекций, касающихся материала рассматриваемого в первом семестре обучения. Названия лекций соответствует определенным разделам курса, по времени чтения некоторые лекции занимают от 4 до 8 учебных часов. Общее число часов, приходящихся на эту часть курса равно 48.
Библиогр.: 25 назв. Рис. 19
Подготовлено кафедрой «Физическая и коллоидная химия»
© ГОУ ВПО «Уральский государственный
технический университет - УПИ», 2006
Содержание
Для перехода нажмите СТRL и щелкните по интересующей лекции
Стр.
| Лекция 1 Основные понятия термодинамики (составитель Степановских Е.И.) | |
| Лекция 2. Первый закон термодинамики. Внутренняя энергия. Энтальпия (составитель Степановских Е.И.) | |
| Лекция 3. Второй закон термодинамики. Энтропия (составители: Степановских Е.И., Брусницына Л.А.) | |
| Лекция 4. Фундаментальное уравнение Гиббса. Энергия Гельмгольца. Энергия Гиббса. Характеристические функции. (составители: Степановских Е.И., Брусницына Л.А., Маскаева Л.Н., Макурин Ю.Н.) | |
| Лекция 5. Термодинамика растворов (составители: Степановских Е.И., Брусницына Л.А., Маскаева Л.Н., Марков В.Ф.) | |
| Лекция 6. Расчет изменений экстенсивных свойств системы за счет протекания в ней химической реакции (составители: Степановских Е.И., Брусницына Л.А., Макурин Ю.Н.) | |
| Лекция 7. Фазовые равновесия в однокомпонентной системе (составители Лундин А.Б., Булатов Н.К.) | |
| Лекция 8. Фазовые равновесия в двухкомпонентной системе «жидкость-пар». (составители Лундин А.Б., Булатов Н.К.) | |
| Лекция 9. Фазовые равновесия в двухкомпонентной системе «твердое вещество-жидкость» (составители Больщикова Т.П., Урицкая А.А.) | |
| Библиографический список |
Лекция 1. Основные понятия термодинамики
Термодинамика возникла как учение о тепловых машинах. Потом выяснилось, что ее основные положения имеют принципиальное значение, и термодинамика выделилась в самостоятельную дисциплину.
Термодинамика как наука отличается рядом особенностей:
1. Это наука дедуктивная, так как исходя из немногих общих положений, применяя их к конкретным частным явлениям, она получает определенные соотношения, относящиеся только к данному явлению
2. Термодинамика имеет дело только с макроскопическими величинами, которые могут быть найдены на опыте.
3. Термодинамика рассматривает процессы вне зависимости от времени и пространства, не касаясь скорости и пути процесса.
Эти особенности термодинамики позволяют применить термодинамический метод в самых различных областях.
В результате химических реакций происходят глубокие изменения физико- химических свойств взаимодействующих веществ при одновременном выделении и поглощении тепла. Необходимо знать законы, определяющие превращение энергии при химическом взаимодействии. Распространение термодинамического метода на изучении химических реакций привело к образованию особого раздела термодинамики − химической термодинамики. То есть с одной стороны химическая термодинамика − это раздел общей термодинамики, а с другой − химическая термодинамика оказывает существенное влияние на развитие всей термодинамики в целом.
В термодинамическом методе условно все объекты материального мира разбиваются на систему и окружающую среду (внешнюю среду).
Система - это тело или группа тел, которые являются предметом исследования. Все остальные тела материального мира − окружающая среда.
Система имеет точные пространственные границы, отделяющие ее от окружающей среды. Причем это могут быть реальные физические поверхности раздела или воображаемая математическая поверхность. Рассматриваемые в физической химии системы − макроскопические, так как только для систем, состоящих из большого количества молекул можно оперировать такими понятиями, как температура, давление, теплота.
В зависимости от признака, общего, характерного для ряда систем, все системы характерного можно подразделить на:
1. По количеству компонентов в системе:
на однокомпонентные (чистое вещество) и многокомпонентные (смесь, раствор).
2. По количеству фаз в системе:
на однофазные (или гомогенные, или однородные) и многофазные (или гетерогенные или неоднородные)
3. По наличие взаимодействия системы с окружающей средой:
на изолированные, открытые и закрытые.
Система полностью лишенная возможности взаимодействовать с окружающей средой называется изолированной. Вообще говоря, это - научная абстракция, так как в природе нет материалов или средств, обладающих абсолютной изолирующей способностью. Но это очень полезная абстракция, которая позволяет создать математическую модель многих процессов, протекающих в действительности.
Условимся обозначать индексом " i " величины, характеризующие процессы, протекающие внутри системы (от латинского слова internal - внутренний), а индексом " е " −величины, характеризующие взаимодействие системы с окружающей средой (этот индекс от латинского слова external - внешний)
Из всего множества взаимодействий выделим два: обмен между системой и окружающей средой энергией (обозначим энергию W) и обмен массой (m).
Запишем словами и математическими символами теперь классификацию систем:
Изолированная система - это такая система, где нет обмена с окружающей средой ни энергией, ни массой, то есть dW=0, dm=0
Открытая система − это такая система, где есть обмен и массой и энергией, то есть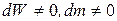 
Закрытая система - это такая система, где есть обмен энергией с окружающей средой, но нет обмена массой, то есть 
4. По наличию химического превращения системы делятся на: системы с химическим превращением и системы без химического превращения.
Компоненты системы могут вступать в тесное взаимодействие друг с другом, при котором происходит преобразование одних компонентов в другие. Это преобразование называется химическим превращением.
Химическое превращениехарактеризуется изменением чисел молей компонентов, причем это изменение не связано с обменом веществом между системой и окружающей средой. То есть, если применить ранее введенные символы, то бесконечно малое изменение чисел молей компонента k, обусловленное участием частиц компонента в химическом превращении, обозначится как 
, а приращение числа молей компонента k, обусловленное массообменом с окружающей средой − как 
.
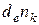Общее приращение числа молей компонента k состоит:
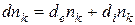(1.1)
Если нет массообмена между системой и окружающей средой, то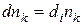 
(1.2)
Если рассматривается система без химического превращения, то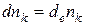 
(1.3)
Здесь следует остановиться на вопросе о термодинамических переменных или термодинамических параметрах или параметрах состояния.
Состояние системы – это совокупность всех физических и химических свойств.
Состояние любой термодинамической системы может быть охарактеризовано количественно с помощью термодинамических переменных. Все они взаимосвязаны, и для удобства построения математического аппарата их условно делят на независимые переменные и термодинамические функции. Переменные, которые фиксированы условиями существования системы, и, следовательно, не могут изменяться в пределах рассматриваемой задачи, называют термодинамическими параметрами. Различают переменные:
Экстенсивные, которые прямо пропорциональны массе системы или числу частиц. Например, объем V, энергия U, энтропия S, теплоемкость С;
Интенсивные, которые не зависят от массы системы или числа частиц, например, температура T, плотность массы r, давление p. Отношение любых двух экстенсивных величин является интенсивным параметром, например, парциальный или мольный объемы, мольная или массовая доля.
Среди термодинамических переменных выделяют обобщенные силы (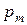
) и обобщенные координаты (
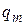). Обобщенные силы характеризуют состояние равновесия. К ним относят давление p, химический потенциал компонента 
, температуру Т; электрический потенциал j. Обобщенные силы – интенсивные параметры.
Обобщенные координаты – это величины, которые изменяются под действием соответствующих обобщенных сил. К ним относятся: объем V; количество вещества nk; заряд q; энтропию S. Все обобщенные координаты – экстенсивные величины.
Различают следующие состояния системы:
Равновесное, когда все характеристики системы постоянны и в ней нет потоков вещества или энергии;
Неравновесное (неустойчивое) состояние, при котором всякое бесконечно малое воздействие вызывает конечное изменение состояния системы;
Стационарное, когда независимые переменные постоянны во времени, но в системе имеются потоки.
Если состояние системы изменяется, то говорят, что в системе происходит термодинамический процесс. Все термодинамические свойства строго определены только в равновесных состояниях. Особенностью описания термодинамических процессов является то, что они рассматриваются не во времени, а в обобщенном пространстве независимых термодинамических переменных, т.е. характеризуются не скоростями изменения свойств, а величинами изменений. Процесс в термодинамике – это последовательность состояний системы, ведущих от одного начального набора термодинамических переменных к другому– конечному.
Различают процессы:
Самопроизвольные, для осуществления которых не надо затрачивать энергию;
Несамопроизвольные, происходящие только при затрате энергии:
Обратимые, когда переход системы из одного состояния в другое и обратно может происходить через последовательность одних и тех же состояний, и после возвращения в исходное состояние в окружающей среде не остается макроскопических изменений;
Квазистатические или равновесные, которые происходят под действием бесконечно малой разности обобщенных сил;
Необратимые или неравновесные, когда в результате процесса невозможно возвратить и систему и ее окружение к первоначальному состоянию.
Термодинамические функции разделяют на
Функции состояния, которые зависят только от состояния системы и не зависят от пути, по которому это состояние получено;
Функции перехода, значение которых зависит от пути, по которому происходит изменение системы.
Примеры функций состояния: энергия, энтальпия, энергия Гиббса, энергия Гельмгольца, объем, давление, температура.
Примеры функций перехода: теплота Q и работа A.
Обозначим какую-либо функцию состояния системы через Е, а независимые переменные (или параметры состояния) через x и y. Запишем некоторые важные свойства функций состояния.
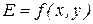
Справедливы следующие свойства Е:
1. 
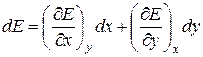(1.4)
где коэффициенты перед приращениями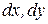 
- частные производные функции Е по аргументу 
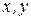при постоянном значении параметров 
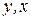соответственно.
2. Очень важное свойство функции состояния заключается в том, что dE можно интегрировать, причем при этом получим:
(1.5)
Интеграл по замкнутому контуру, то есть изменение функции состояния в круговом процессе, равно 0: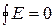 
Условие установления равновесия:
если выделить некоторую материальную систему и оградить ее от взаимодействия с окружающей средой, то по истечении некоторого времени в системе прекратятся какие-то бы ни было процессы. Наступит состояние макроскопического равновесия. Это состояние может быть нарушено только внешним воздействием.
Одним из постулатов термодинамики является утверждение:
Если система А находится в тепловом равновесии с системой В, а та, в свою очередь, находится в равновесии с системой С, то системы А и С также находятся в тепловом равновесии.
Лекция 2. Первый закон термодинамики. Внутренняя энергия. Энтальпия
Рассматриваемые нами системы состоят из большого количества частиц (атомов, молекул, ионов), находящихся в непрерывном движении. В соответствии с формой движения частиц различают поступательную и вращательную энергию молекул, колебательную энергию атомов и групп атомов в молекуле, энергию движения электронов, внутриядерную и другие виды энергии.
Внутренняя энергия является частью полной энергии (в полную энергию входят кинетическая энергия, потенциальная энергия и внутренняя энергия).
Внутреннюю энергию принято обозначать заглавной латинской буквой U.
Внутренняя энергия системы зависит от природы вещества, его массы, параметров состояния системы. Внутренняя энергия – экстенсивное свойство. Из физики известно, что внутренняя энергия идеального газа не зависит от давления, объема, а определяется лишь изменением температуры.
Внутренняя энергия является функцией состояния, то есть изменение ее не зависит от промежуточных стадий пути, а определяется лишь значением внутренней энергии в начальном состоянии и значением внутренней энергии в конечном состоянии.
Это положение вытекает из закона сохранения энергии, согласно которому энергия не исчезает и не возникает вновь из ничего при протекании процесса, она лишь может переходить из одной формы в другую в строго эквивалентных количествах.
Раз внутренняя энергия функция состояния, то бесконечно малое изменение ее – полный или точный дифференциал.
Абсолютное значение внутренней энергии, равно как и величин, в определительные формулы которых она входит, найти нельзя, так как нельзя даже мыслимо представить себе нулевой уровень внутренней энергии. В связи с этим при расчетах всегда оперируют изменениями внутренней энергии.
Наряду с внутренней энергией в термодинамике при рассмотрении многих процессов удобно использовать такую функцию, как энтальпия, она обозначается латинской заглавной буквой H и определительное выражение для энтальпии имеет вид:
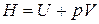(2.1)
где U – внутренняя энергия системы, р – давление системы, V - объем системы. Так как в правой части уравнения все функции являются функциями состояния, то и сама энтальпия тоже является функцией состояния, то есть ее изменение не зависит от пути протекания этого изменения, а определяется лишь значением энтальпии в начале процесса и в конце процесса. Следовательно, бесконечно малое изменение энтальпии будет полным дифференциалом. Энтальпия имеет ту же размерность, что и внутренняя энергия, это тоже экстенсивное свойство, то есть оно зависит от массы системы.
В принципе и внутреннюю энергию, и энтальпию можно рассматривать как функцию любых независимых переменных, любых параметров состояния. Естественно, что в случае одного набора переменных мы получим лаконичные и удобные уравнения состояния, в случае другого набора переменных мы тоже получим уравнения состояния, но они будут громоздкими, неудобными для экспериментальной проверки, с неопределяемыми на опыте коэффициентами. Поэтому принято рассматривать каждую функцию относительно какого-то определенного набора переменных, которые можно назвать естественными для данной функции. Такими переменными для внутренней энергии можно считать объем системы V, энтропию S и химическую переменную ξ, если в системе идет химическое превращение. Для энтальпии такой набор переменных следующий: давление р, энтропия S и глубина реакции ξ.
Рассмотрим систему, взаимодействующую с окружающей средой. Внутренняя энергия системы U. Тогда за счет взаимодействия внутренняя энергия системы изменилась на величину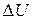 
. По закону сохранения энергии на такую же величину изменилась энергия тех тел окружающей среды, с которыми система взаимодействовала.
Естественно, что нам надо располагать общими для разных взаимодействий количественными мерами.
Принято, количество воздействия, характеризующее разный тип взаимодействий системы с окружающей средой, а именно тепловое взаимодействие, механическое, массовое, электрическое, магнитное, сил поверхностного натяжения и т.д. называть словом работа.
Работа – это общая мера для количественной оценки воздействий разной природы.
Работа характеризует разные по природе взаимодействия системы с окружающей средой. То есть теплота это часть термической работы.
В общем виде величина элементарной работы (то есть работы совершенной при переносе через некоторый участок поверхности ограничивающей систему от окружающей среды) бесконечно малой величины обобщенной координаты под действием обобщенного потенциала может быть найдена следующим образом:
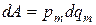(2.2)
где – 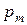– обобщенный потенциал разных взаимодействий, то есть в частном случае механического взаимодействия это отрицательное давление внутри системы, а 
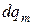– это дифференциал обобщенной координаты, то есть той величины, которая переносится от системы к окружающей среде в процессе взаимодействия.
Рассмотрим конкретные виды работ. Пусть у нас есть однородная система (то есть такая система, в которой в каждой ее точке свойства одинаковы) вступающая в механическое, массовое и термическое взаимодействие с окружающей средой.
В механическом взаимодействии работа равна
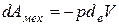(2.3)
где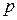 
− внешнее давление, а 
– соответствующий механический потенциал системы,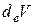 
−изменение объема системы.
В термическом взаимодействии величина работы может быть найдена как
(2.4)
где Т − температура системы, 
− приращение энтропии системы за счет внешних причин.
Принято рассматривать величину полного приращения энтропии системы как сумму, в которой первое слагаемое обусловлено теплообменом (то есть хаотическим движением частиц, не связанным с переносом массы через границу системы), а второе − массообменом между системой и окружающей средой:
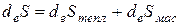(2.5)
Привлекая выражение (2.5) в уравнение (2.4), получаем
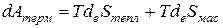(2.6)
В этом соотношении первое слагаемое, то есть часть термической работы, обусловленная только тепловым взаимодействием, называется теплотой. Именно ее обозначают буквой Q и справедливо следующее соотношение
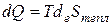(2.7)
Термическая работа совпадает с теплотой только в случае закрытой системы, где 
равно нулю.
Следует отметить очень важный момент: и величина работы и количество теплоты характеризуют энергию, переданную в результате взаимодействия системы с окружающей средой. От того, каким образом происходило это взаимодействие, зависит размер работы или количество теплоты. То есть и теплота и работа являются функциями, зависящими от процесса перехода системы от одного состояния в другое, но не функциями состояния. Поэтому бесконечно малое изменение их не является полным дифференциалом.
Выбрана система знаков, учитывающая увеличение внутренней энергии, то есть то, что увеличивает внутреннюю энергию, считается положительным, то, что уменьшает − отрицательным. Значит, если теплота подводится к системе, и система получает теплоту – то эта теплота положительна. Если же система отдает теплоту в окружающую среду, то теплота отрицательна. Так же и с работой. Если работа осуществляется над системой, то есть увеличивает внутреннюю энергию системы, то она положительна. Если же работу совершает сама система над окружающей средой, то при этом запас внутренней энергии уменьшается, а значит эта работа отрицательна.
Работу можно выразить через свойства системы, но сама работа не является каким-либо свойством системы, равно как и свойством окружающей среды. Работа совершается в результате взаимодействия системы с окружающей средой и прекращается с окончанием взаимодействия.
В случае массового взаимодействия совершается массовая работа
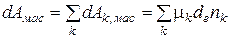(2.8)
Первый закон термодинамики
Первый закон термодинамики – это фактически закон сохранения энергии. Он утверждает, что
Существует аддитивная функция состояния термодинамической системы, называемая внутренней энергией U. Энергия изолированной системы постоянна.
Первый закон термодинамики носит постулативный характер. Он базируется на многочисленных опытах. Его верность проверяется путем сопоставления вытекающих из него следствий с опытом. Пока в истории науки не найдено опытных данных, противоречащих этому закону.
1 закон термодинамики вводит понятие внутренней энергии системы и утверждает, что изменение внутренней энергии системы равно количеству энергии, полученной системой из внешнего мира, из окружающей среды в течение рассматриваемого промежутка времени.
Опыт показывает, что несмотря на то, что каждая в отдельности работа (соответствующая какому-либо виду взаимодействия) зависит от пути процесса, суммарная работа не зависит от этого пути, а определяется только начальным и конечным состоянием системы. То есть сумма всех элементарных работ, совершаемых системой и над системой, является полным дифференциалом некоторого присущего системе свойства, называемого внутренней энергией и обозначаемого буквой U. Математическая запись первого закона термодинамики (или первого начала термодинамики) следовательно будет иметь вид:
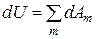(2.9)
где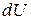 
дифференциал внутренней энергии, а под знаком суммы приведены элементарные работы, произведенные при разных взаимодействиях системы с окружающей средой.
Интегрирование уравнения (2.9) дает
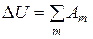(2.10)
Причем изменение внутренней энергии найдется как разность между значениями внутренней энергии в состоянии одни и значением внутренней энергии в состоянии 2.
. (2.11)
Привлечем в выражение (2.11) ранее записанное выражение для работы в общем виде (2.2):
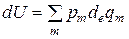(2.12)
Из этого выражения можно видеть, что внутреннюю энергию можно рассматривать в виде некоторой функции обобщенных координат. Если систему изолировать от окружающей среды, то есть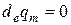 
, то изменение внутренней энергии становится невозможным. Справедлива такая формулировка:
Энергия изолированной системы постоянна.
Математически это можно записать так:
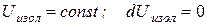(2.13)
Утверждение о том, что у всякой изолированной системы внутренняя энергия остается постоянной, называется законом сохранения внутренней энергии.
Для закрытой системы при только механическом и термическом взаимодействии системы с окружающей средой:
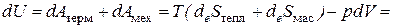
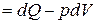(2.14)
Лекция 3. Второй закон термодинамики. Энтропия
Энтропия, обозначаемая буквой S, экстенсивное свойство системы, была введена Клаузиусом, при анализе материала по тепловым двигателям, первоначально в виде так называемой "приведенной теплоты"− то есть математически:
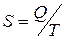(3.1)
где Q - количество тепла, которым обменивается система с окружающей средой при совершении обратимого процесса.
Исходя из этой формулы, легко видеть размерность энтропии: [ Дж/К ], а если мы рассматриваем мольную величину, то [ Дж/(моль К) ]. Повторим, что значит экстенсивная величина. Это значит, что энтропия всей системы может быть найдена суммированием значений энтропий всех составных частей системы:
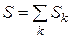(3.2)
Клаузиусом было доказано, что несмотря на то, что теплота зависит от пути процесса, величина отношения теплоты к абсолютной температуре, не зависит от пути процесса, то есть является функцией состояния. Эта функция состояния была названия энтропией. Бесконечно малое изменение энтропии является полным дифференциалом. Конечное же изменение энтропии в результате какого-то процесса может быть найдено, как
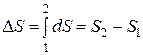(3.3)
Совмещая выражение (3.3) с определительным для энтропии выражением, записанным для бесконечно малых величин
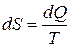(3.4)
запишем общую формулу для расчета изменения энтропии в ходе процесса:
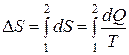(3.5)
Формулы (3.3), (3.4), (3.5) − основные формулы для расчета энтропии. Раскрыв смысл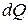 
в каждом конкретном случае можно рассчитать и 
.
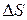Формула (3.4) в то же время является математическим выражением классической формулировки 2 закона термодинамики, который гласит, что для всех обратимых изменений в закрытой системе с однородной температурой справедливо соотношение
.
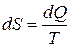Для всех необратимых изменений в закрытой системе величина приращения энтропии будет больше, чем изменение приведенной теплоты, то есть
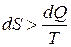. (3.6)
Эти соотношения можно записать в виде неравенства Клаузиуса, которое связывает изменение энтропии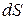 
с количеством теплоты 
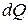, которым система обменивается с окружением при температуре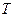 
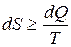. (3.7)
Причем знак равенства имеет место при обратимых, а неравенства – при необратимых процессах.
Источниками необратимых процессов могут быть: диффузия, расширение системы при существовании разности давлений между ней и окружающей средой, теплопередача при разных температурах, самопроизвольные химические реакции в объеме системы и другие диссипативные процессы, связанные с необратимым превращением работы в теплоту. Неравенство (3.7) выполняется независимо от причины возникновения необратимого процесса, в итоге наблюдается выделение внутри системы дополнительного количества теплоты. Р.Клаузиус назвал эту теплоту, вызванную неравновесными процессами, некомпенсированной теплотой (обозначим эту величину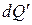 
).
Известно, что если процесс осуществляется равновесно и обратимо, то совершаемая работа – максимальна. Если процесс осуществляется необратимо, то работа оказывается меньше, чем в обратимом процессе, часть ее как бы «теряется». В соответствии с первым законом термодинамики «потерянная» работа должна проявиться в другой форме, например, в форме некомпенсированной теплоты, которая всегда неотрицательна: больше нуля в необратимых, равна нулю в обратимых процессах.
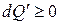(3.8)
При изотермических процессах неравенство (3.7) можно записать в виде равенств:
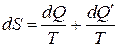(3.9)
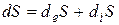, (3.10)
где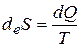 
- изменение энтропии, вызванное равновесным теплообменом с окружающей средой (индекс «e » от лат. external - внешний);
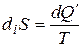- рост энтропии из-за необратимых процессов внутри системы (индекс «i » от лат. internal – внутренний).
Величину энтропии данной системы нельзя измерить непосредственно на опыте, но ее можно вычислить, пользуясь формулой (3.3)
Эта формула позволяет найти не абсолютную величину энтропии, а разности энтропий в двух состояниях системы, т.е. изменение энтропии при переходе системы из состояния 1 в состояние 2.
Термин "некомпенсированная теплота" не совсем удачен. Теплота это энергия, которой система обменивается с внешним миром и следовательно, которая проходит через поверхность ограничивающую систему от внешнего мира. А та теплота, которую Клаузиус назвал некомпенсированной, возникает вследствие протекания процессов внутри самой системы.
Прежде чем мы запишем современную формулировку 2 закона термодинамики, отметим, что этот закон, также как и 1 закон постулативный. Он не выведен теоретически, а просто постулирован, на основании осмысления огромного экспериментального материала накопленного за человеческую историю. Правильность его подтверждается соответствием следствий из него практике. И пока нет таких экспериментов, которые бы его опровергли. Хотя попыток предпринималось очень много.
Запишем формулировку второго закона термодинамики:
у всякой изолированной системы, находящейся в неравновесном состоянии, энтропия с течением времени возрастает, ее рост продолжается до тех пор, пока система не достигнет равновесного состояния.
Это и есть второй закон термодинамики или как его еще называют закон возрастания энтропии. Математически его можно записать в форме:
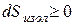
где знак неравенства относится к неравновесному состоянию, а знак равенства к равновесному.
Из выражения (3.10) следует, что энтропия изолированной системы может только возрастать, но никогда не может уменьшаться.
Существует также формулировка второго закона термодинамики, сформулированная Клаузиусом:
Энергия мира постоянная, энтропия мира стремится к максимуму.
Уже во время формулировки второго закона термодинамики многие ученые пришли к заключению о механико-молекулярной природе тепла (Джоуль, Клаузиус, Больцман). В основе этого подхода лежит фундаментальное положение о том, что внутренняя энергия газа сводится к кинетической энергии движения его молекул. Однако движения отдельных молекул не могут быть учтены, так как молекул много, скорости движения их высоки, они постоянно меняют направления. Вполне можно охарактеризовать тепловое движение понятием молекулярного хаоса и применить для его изучения статистические законы. На основе этого представления можно полагать, что разделив весь объем газа на большое количество элементарных объемов (по величине значительно больших, чем размер молекул), мы получим одинаковое число молекул в каждом, так как распределение молекул по скоростям одинаково для всех объемов, а число входящих молекул в объем практически равно числу выходящих. Все это привело Людвига Больцмана к заключению о взаимосвязи между энтропией и вероятностью.
Действительно, всякая система развивается так, что ее энтропия возрастает. С другой стороны это развитие самопроизвольно, направлено в сторону наиболее вероятного с точки зрения энергетической устойчивости состояния. То есть уже на уровне умозаключений можно предположить, что энтропия является функцией вероятности, то есть
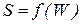(3.11)
где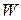 
− вероятность состояния системы, а 
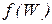некоторая возрастающая функция.
Что такое термодинамическая вероятность состояния системы.
Если мы знаем давление, объем и температуры системы, то мы говорим о каком-то макроскопическом состоянии системы, но не можем судить о положении в пространстве и скорости отдельных молекул.
Состояние каждой молекулы вообще определяется шестью параметрами: три координаты положения и три составляющие скорости), если молекул N, то параметров будет 6N. Но поскольку состояние коллектива молекул зависит не от направления скоростей, а от кинетической энергии молекул,то макроскопическое состояние коллектива молекул N зависит от меньшего числа параметров и может быть характеризовано некоторым числом комплексий, каждая из которых характеризует определенное распределение, при котором каждая различимая молекула имеет данную кинетическую энергию. Число комплексий, позволяющих реализовать данное состояние, есть термодинамическая вероятность этого состояния. Она рассчитывается по числу молекул по определенным формулам.
Людвиг Больцман нашел количественно зависимость между энтропией и термодинамической вероятностью состояния:
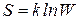(3.12)
и определил физический смысл коэффициента: 
Этот коэффициент теперь называется постоянной Больцмана.
Расчет изменения энтропии при изменении температуры системы
Изменение энтропии вещества, температура которого, например, повышается при постоянном объеме от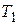 
до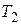 
, вычисляют путем интегрирования частной производной энтропии по температуре при постоянном объеме
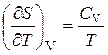, (3.13)
где 
− изохорная теплоемкость системы, Дж/К.
Если в системе в указанном диапазоне температур не происходит каких-либо фазовых превращений, то интегрирование (3.13) приводит к:
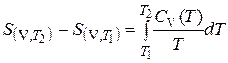(3.14)
Изменение энтр