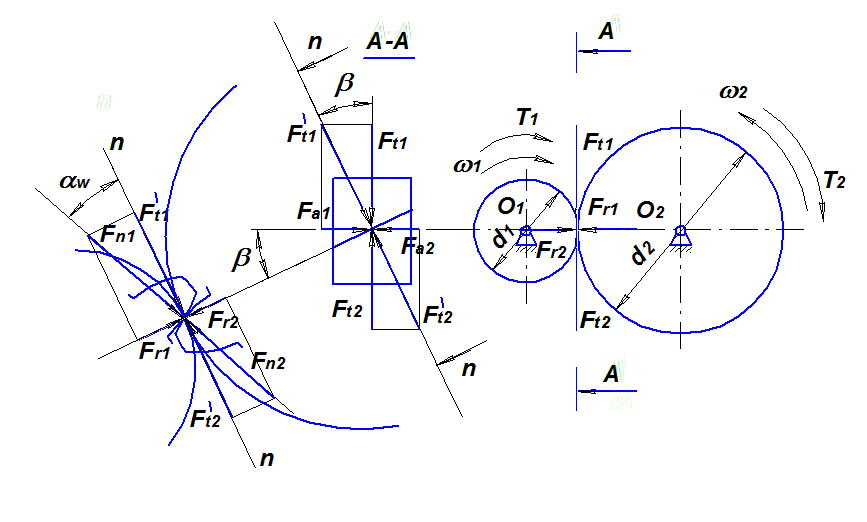
Рис.2.1. Схема сил в зацеплении цилиндрической косозубой передаче
Окружная сила (рис. 2.1):
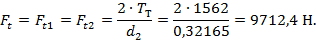
| (2.19) |
Радиальная сила:
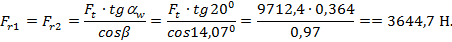
| (2.20) |
Осевая сила:
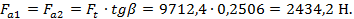 (2.21)
Нормальная сила (2.21)
Нормальная сила
|
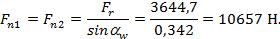
Проверка зубьев передачи по контактным напряжениям и
Напряжениям изгиба
1. Проверка зубьев передачи по контактным напряжениям
Условие прочности 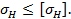
Определяем расчётное контактное напряжение
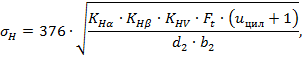
| (2.22) |
где
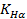 - коэффициент, учитывающий распределения нагрузки между зубьями, определяем в зависимости от окружной скорости и степени точности передачи, по табл. 2.7.
- коэффициент, учитывающий распределения нагрузки между зубьями, определяем в зависимости от окружной скорости и степени точности передачи, по табл. 2.7.
Таблица 2.7
Значение 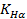 и
и 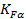 для косозубых и шевронных передач
для косозубых и шевронных передач
| Степень точности | 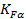
| 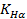
| ||||
| Окружная скорость V, м/с. | ||||||
| до1 | ||||||
| 0,72 0,81 0,91 1,0 | 1,02 1,06 1,1 | 1,02 1,05 1,09 1,16 | 1,03 1,07 1,13 - | 1,04 1,10 - - | 1,05 1,12 - - | |
Примечание: для прямозубых колес 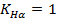 , , 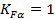
|
Принимаем 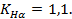
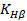 - коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого колеса, определяем по табл. 2.8.
- коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого колеса, определяем по табл. 2.8.
Принимаем 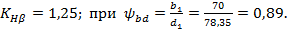
Коэффициент, учитывающий внутреннюю динамическую нагрузку 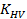 определяем по табл. 2.9.
определяем по табл. 2.9.
Принимаем 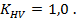
Определяем расчетное контактное напряжение:

|
Т.к. 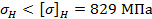 , то условие прочности по контактным напряжениям выполнено. При несоблюдении этого условия изменяют
, то условие прочности по контактным напряжениям выполнено. При несоблюдении этого условия изменяют 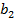 или
или 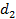 (и, следовательно
(и, следовательно 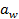 ).
).
2. Проверка зубьев передачи по напряжениям изгиба
Определяем расчётное изгибающее напряжение в зубьях колеса:
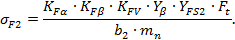
| (2.23) |
Расчетное изгибающее напряжение в зубьях шестерни:
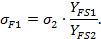
| (2.24) |
Выбираем коэффициенты, необходимые для проверки колес по изгибающим напряжениям.
Коэффициент, учитывающий распределение нагрузки между зубьями (табл. 2.7): 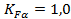 .
.
Коэффициент, учитывающий внутреннюю динамическую нагрузку (табл. 2.9): 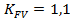 .
.
Определяем коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
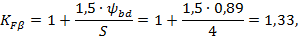
| (2.25) |
здесь S = 4 - индекс схемы (тот же, что и в формуле 2.13).
Определяем коэффициент, учитывающий наклон зуба 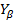 :
:
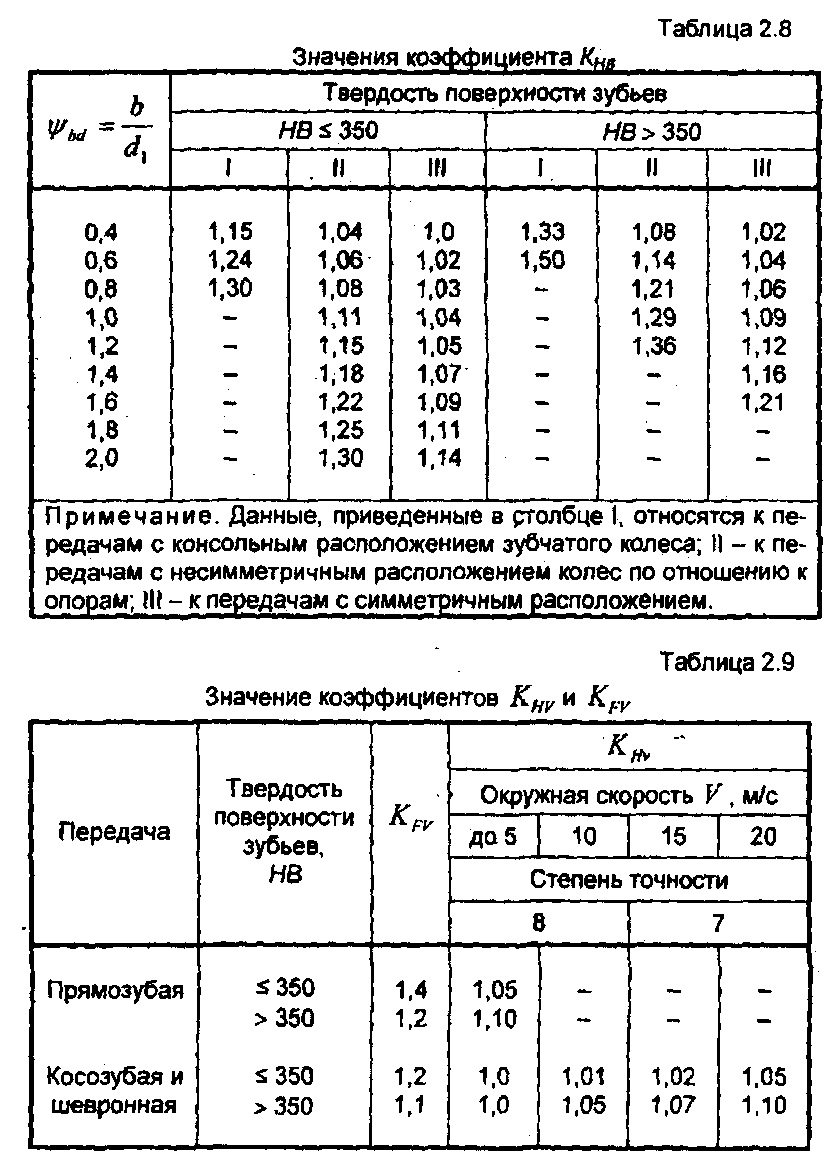
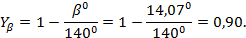
|
Определяем приведённое число зубьев колеса:
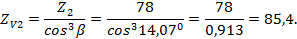
|
По табл. 2.10, в зависимости от 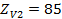 , принимаем коэффициент
, принимаем коэффициент 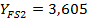 , учитывающий форму зуба и концентрацию напряжений.
, учитывающий форму зуба и концентрацию напряжений.
Для шестерни:
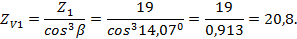
|
Таблица 2.10
Значения коэффициента 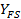 для внешнего зацепления без смещения
для внешнего зацепления без смещения
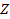 или или 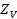
| |||||||
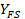
| 4,3 | 4,08 | 3,98 | 3,92 | 3,88 | 3,84 | 3,8 |
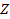 или или 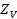
| 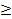 100 100
| ||||||
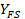
| 3,75 | 3,7 | 3,66 | 3,65 | 3,62 | 3,61 | 3,6 |
По табл. 2.10 принимаем 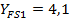 .
.
Определяем расчётное изгибающее напряжение в зубьях колеса:
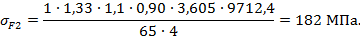
|
Расчетное изгибающее напряжение в зубьях шестерни:
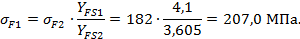
|
Т.к. соблюдаются требования:
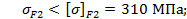
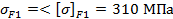 , то условие прочности по изгибающим напряжениям выполнено.
, то условие прочности по изгибающим напряжениям выполнено.
Расчёт конической передачи
Выбор материала, термической обработки и расчёт
Допускаемых напряжений
Материалы для изготовления зубчатых колёс подбирают по табл. 2.1.
Из табл. 2.1 и для шестерни и для колеса выбираем сталь 40Х, термообработку - улучшение и закалка ТВЧ. Соотношение единиц твердости по Роквеллу (HRC) и единиц твёрдости по Бринеллю (НВ) принимаем по табл. 2.2. Твердость шестерни HRC153 (HB1 522), твердость колеса HRC2 248 (НВ2460).
Средняя твердость рабочих поверхностей зубьев:
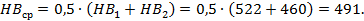
|
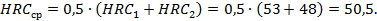
|
Базовые числа циклов нагружений:
- при расчете на контактную прочность

|
- при расчете на изгиб:

|
Время работы передачи в часах 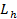 ; при числе лет
; при числе лет  коэффициенте годового использования
коэффициенте годового использования  и коэффициенте суточного использования
и коэффициенте суточного использования 
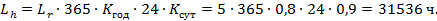
|
Действительные числа циклов перемены напряжений:
- для шестерни
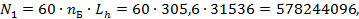
| |
| - для колеса | |
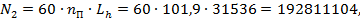
|
Коэффициент долговечности при расчете по контактным напряжениям:

 для материалов с однородной структурой; для материалов с однородной структурой;
 для материалов поверхностно упрочнённых; для материалов поверхностно упрочнённых;
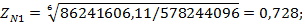
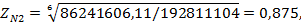 таким образом, принимаем
таким образом, принимаем 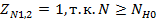 . .
|
Коэффициент долговечности при расчете на изгиб:
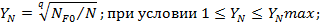
 для улучшенных зубьев колёс; для улучшенных зубьев колёс;
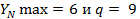 для закалённых и поверхностно-упрочнённых зубьев для закалённых и поверхностно-упрочнённых зубьев
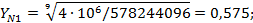
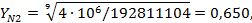 таким образом, принимаем
таким образом, принимаем 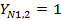 , т.к. , т.к. 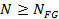
|
По таблице 2.3 рассчитываем:
-предел контактной выносливости зубьев при базовом числе
циклов:

| |
| - предел выносливости зубьев при изгибе при базовом числе циклов: | |

|
Определяем допускаемые контактные напряжения для шестерни и колеса:

| |
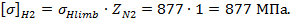
|
Определяем допускаемые напряжения изгиба для шестерни и колеса:

| |

|
Допускаемое рабочее контактное напряжение для косозубых колес:
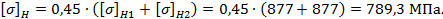
|