Методические разработки проведения практических занятий
С элементами УИРС по дисциплине
«Методология научной деятельности в лесном
И лесопарковом хозяйстве»
Занятие № 5
Тема: «Исследование эффективности статистического анализа и его применение в научных исследованиях в лесном хозяйстве»
Ключевые слова: генеральная совокупность, среднее арифметическое, ошибка репрезентативности среднего, стандартное отклонение, коэффициент вариации, показатель точности опыта, критерий достоверности Стьюдента.
Бюджет времени – 2 часа.
Количество двухчасовых занятий – 1.
Распределение бюджета времени:
- 1 час на освоение теоретических основ вычисления описательных статистик;
- 1 час на практическое освоение расчета статистических показателей в электронных таблицах Microsoft Excel.
Вводная часть
Исчерпывающей характеристикой любой случайной величины является закон её распределения. Однако такая характеристика слишком громоздка и неудобна для получения практических результатов. По этой причине при изучении явлений или процессов рассчитывают только основные числовые характеристики соответствующих случайных величин – основные статистики. Дидактический материал, необходимый для проведения данной лабораторной работы, приведен приведен в файле Excel – «Производные признаки» (Приложение - 3).
Термины, понятия и определения
Среднее арифметическое (М) является основной характеристикой статистической совокупности и отражает уровень, по отношению к которому колеблются значения вариант в ней (Зайцев, 1984).
Генеральной совокупностью называется вся совокупность особей изучаемого объекта. Большинство биометрических исследований проводятся на некоторой части генеральной совокупности (эта часть называется выборкой). Статистические показатели, полученные по выборке распространяются затем на всю генеральную совокупность данного объекта.
|
|
Ошибка репрезентативности ( m ) показывает допустимое отклонение среднего значения признака в ту или другую сторону.
Стандартное отклонение (σ) характеризует степень отклонения вариант данной совокупности от среднего арифметического в абсолютных величинах.
Коэффициент вариации (С v ) показывает, какой процент составляет стандартное отклонение от средней арифметической, и позволяет сравнить между собой по степени варьирования любые совокупности.
Показатель точности опыта (Р) выражает величину ошибки средней арифметической в процентах от самой средней арифметической и, служит показателем точности её определения.
Критерий достоверности Стьюдента ( t ) выражается в долях ошибки репрезентативности выборки, принятой за 1. Расчетное значение критерия сравнивается с его табличным значением (при числе степеней свободы (n – 1) и делается вывод о достоверности полученных результатов.
Порядок проведения занятия
1. Преподаватель объясняет студентам необходимость проведения статистического анализа при планировании научных исследований и знакомит с основными статистическими показателями, применяемыми для оценки достоверности полученных данных.
2. Преподаватель приводит формулы для расчета статистических показателей.
|
|
3. Преподаватель объясняет особенности проведения статистического анализа в электронных таблицах Microsoft Excel.
4. Преподаватель выдает индивидуальное задание студентам для расчета статистических показателей.
Порядок выполнения задания:
На первом этапе рассчитывают средние значения признаков в группе анализируемых объектов (отобранных видов лиственницы или плюсовых деревьев сонны обыкновенной). Применяем общепринятый алгоритм расчетов с определением следующих основных статистических показателей:
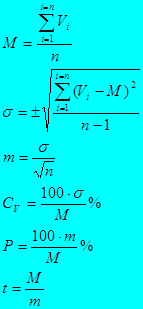
Где:
M – среднее арифметическое значение признака или математическое ожидание;
m – ошибка репрезентативности выборочного среднего (абсолютная ошибка);
σ – среднеквадратическое отклонение или стандартное отклонение (в некоторых публикациях обозначается символом S);
Cv – коэффициент вариации, выражается в процентах;
P – точность опыта (относительная ошибка, выражается в процентах;
t – критерий достоверности Стьюдента.
На втором этапе при достаточной точности и достоверности полученных статистических результатов (точность опыта должна быть в пределах 5%, а критерий Стьюдента не менее величины соответствующего табличного значения для установленного числа степеней свободы) признаем оценки средних значений признаков в группе отобранных видов достоверными. Об этом делают соответствующую запись в тетради.
2. Смысловое содержание используемых величин
2.1. Математическое ожидание или среднее значение:
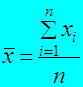
Где:
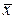- математическое ожидание или среднее значение признака;
|
|
хi= х1, х2, х3, … хn – реализации (даты, количественные значения) получаемые в результате проведения опытов
n – численность совокупности – количество учтенных наблюдений, замеров;
i – порядковый номер единицы учета в совокупности.
Величина 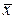определяет место расположения «центра тяжести» статистической совокупности на числовой оси. Название «математическое ожидание» связано с тем, что 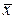служит центром ожидаемой концентрации возможных значений случайной величины.
2.2. Дисперсия S2 или средний квадрат отклонений характеризует рассеивание случайной величины около её среднего значения.
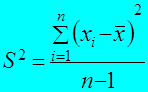
Где:
S2 – дисперсия (в некоторых публикациях обозначается символом σ2);
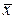- математическое ожидание или среднее значение признака;
хi= х1, х2, х3, … хn – реализации (даты, количественные значения) получаемые в результате проведения опытов;
n – численность совокупности – количество учтенных наблюдений, замеров;
i – порядковый номер единицы учета в совокупности.
2.3. Ввиду того, что размерность дисперсии не совпадает с размерностью изучаемой случайной величины – равна её квадрату, более удобной и приемлемой характеристикой величины рассеяния является среднеквадратическое отклонение, определяемое формулой (соотношением):
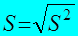
Сравнение двух случайных величин или двух статистических совокупностей по величине среднеквадратического отклонения правомерно лишь при условии, что их математические ожидания – средние значения – равны.
2.4. В общем случае (когда математические ожидания могут быть и не равны между собой) для сравнения необходимо использовать коэффициент вариации (Cv):
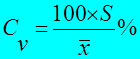
Величина Cv показывает, какую долю от среднего арифметического составляет среднеквадратическое отклонение. Эта величина может быть выражена в долях от среднего – безразмерной статистики, так и в процентах, тогда в формулу вводится коэффициент «100».
2.5. Для характеристики асимметрии распределения – распределения значений случайной величины относительно – можно использовать коэффициент асимметрии (A):
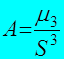
Где:
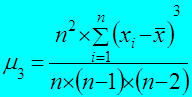
При А >0 асимметрия положительная (левая), при А<0 – отрицательная – правая. По величине коэффициента асимметрии можно судить о преобладании в выборке относительно малых значений случайной величины (А >0) или – больших (А<0).
2.6. Степень заостренности распределения случайной величины можно характеризовать при помощи показателя эксцесса (Е):
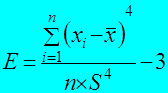
2.7. Для среднего значения, коэффициента асимметрии и показателя эксцесса рассчитывают и их среднеквадратические ошибки:
Ошибка среднего:
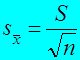
Ошибка коэффициента асимметрии:
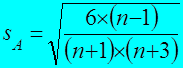
Ошибка показателя эксцесса:
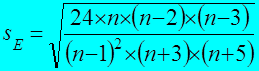
Среднеквадратические ошибки указывают на возможную амплитуду изменений соответствующих показателей (статистик), вычисленных по n опытным значениям.
2.8. Для характеристики точности опыта (выполненного эксперимента или наблюдения) рассчитывают так называемый показатель точности опыта:
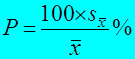
Показатель иногда называют относительной ошибкой. Вместе с тем некоторые специалисты (Лейтас и др., 1983, стр. 23) сомневаются в «полезности» использования данного показателя с целью оценок точности опыта на том основании, что значение оценки Р непосредственно зависит от величины математического ожидания (среднего значения) самой статистической совокупности, подвергаемой статистическому анализу. Однако несостоятельность таких «опасений» авторов очевидна: на стр. 22 ими приведены формулы, в расчетах которых предусмотрены аналогичные схемы отношений некоторого параметра к среднему значению признака в статистической совокупности (коэффициент вариации).