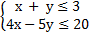Решить систему линейных неравенств – это значит найти множество точек плоскости, которые удовлетворяют каждому неравенству системы.
В качестве простейших примеров рассмотрим системы неравенств, определяющих координатные четверти прямоугольной системы координат («рисунок двоечников» находится в самом начале урока):
Система неравенств 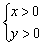 задаёт первую координатную четверть (правая верхняя). Координаты любой точки первой четверти, например,
задаёт первую координатную четверть (правая верхняя). Координаты любой точки первой четверти, например,  и т.д. удовлетворяют каждому неравенству данной системы.
и т.д. удовлетворяют каждому неравенству данной системы.
Аналогично:
– система неравенств 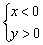 задаёт вторую координатную четверть (левая верхняя);
задаёт вторую координатную четверть (левая верхняя);
– система неравенств  задаёт третью координатную четверть (левая нижняя);
задаёт третью координатную четверть (левая нижняя);
– система неравенств  задаёт четвёртую координатную четверть (правая нижняя).
задаёт четвёртую координатную четверть (правая нижняя).
Система линейных неравенств может не иметь решений, то есть, быть несовместной. Снова простейший пример:  . Совершенно очевидно, что «икс» не может одновременно быть больше трёх и меньше двух.
. Совершенно очевидно, что «икс» не может одновременно быть больше трёх и меньше двух.
Решением системы неравенств может являться прямая, например: 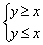 . Лебедь, рак, без щуки, тянут воз в две разные стороны. Да воз и ныне там – решением данной системы является прямая
. Лебедь, рак, без щуки, тянут воз в две разные стороны. Да воз и ныне там – решением данной системы является прямая  .
.
Но самый распространённый случай, когда решением системы является некоторая область плоскости. Область решений может быть не ограниченной (например, координатные четверти) либо ограниченной. Ограниченная область решений называется многоугольником решений системы.
Пример 7
Решить систему линейных неравенств
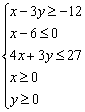
На практике в большинстве случаев приходится иметь дело с нестрогими неравенствами, поэтому оставшуюся часть урока водить хороводы будут именно они.
Решение: то, что неравенств многовато, пугать не должно. Сколько может быть неравенств в системе? Да сколько угодно. Главное, придерживаться рационального алгоритма построения области решений:
1) Сначала разбираемся с простейшими неравенствами. Неравенства  определяют первую координатную четверть, включая границу из координатных осей. Уже значительно легче, так как область поиска значительно сузилась. На чертеже сразу отмечаем стрелочками соответствующие полуплоскости (красные и синие стрелки)
определяют первую координатную четверть, включая границу из координатных осей. Уже значительно легче, так как область поиска значительно сузилась. На чертеже сразу отмечаем стрелочками соответствующие полуплоскости (красные и синие стрелки)
2) Второе по простоте неравенство  – здесь отсутствует «игрек». Во-первых, строим саму прямую
– здесь отсутствует «игрек». Во-первых, строим саму прямую 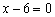 , а, во-вторых, после преобразования неравенства к виду
, а, во-вторых, после преобразования неравенства к виду 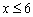 , сразу становится понятно, что все «иксы» меньше, чем 6. Отмечаем зелёными стрелками соответствующую полуплоскость. Ну что же, область поиска стала ещё меньше – такой не ограниченный сверху прямоугольник.
, сразу становится понятно, что все «иксы» меньше, чем 6. Отмечаем зелёными стрелками соответствующую полуплоскость. Ну что же, область поиска стала ещё меньше – такой не ограниченный сверху прямоугольник.
3) На последнем шаге решаем неравенства «с полной амуницией»:  . Алгоритм решения мы подробно рассмотрели в предыдущем параграфе. Вкратце: сначала строим прямую, потом с помощью подопытной точки находим нужную нам полуплоскость.
. Алгоритм решения мы подробно рассмотрели в предыдущем параграфе. Вкратце: сначала строим прямую, потом с помощью подопытной точки находим нужную нам полуплоскость.
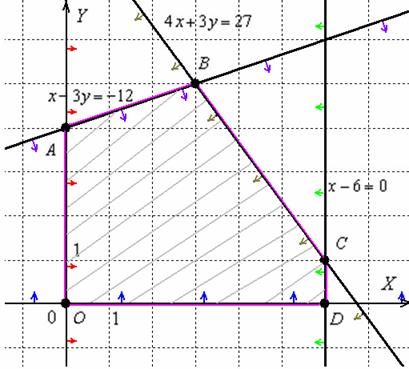
Область решений системы представляет собой многоугольник 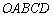 , на чертеже он обведён малиновой линией и заштрихован. Перестарался немного =) В тетради область решений достаточно либо заштриховать, либо жирнее обвести простым карандашом.
, на чертеже он обведён малиновой линией и заштрихован. Перестарался немного =) В тетради область решений достаточно либо заштриховать, либо жирнее обвести простым карандашом.
Любая точка данного многоугольника удовлетворяет КАЖДОМУ неравенству системы (для интереса можете проверить).
Ответ: решением системы является многоугольник 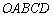 .
.
Пример 9
Решить систему и найти координаты вершин полученной области

Решение: изобразим на чертеже область решений данной системы. Неравенство  задаёт левую полуплоскость с осью ординат, и халявы тут больше нет. После расчётов на чистовике/черновике или глубоких мыслительных процессов, получаем следующую область решений:
задаёт левую полуплоскость с осью ординат, и халявы тут больше нет. После расчётов на чистовике/черновике или глубоких мыслительных процессов, получаем следующую область решений:

Область решений представляет собой многоугольник 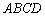 . Теперь нужно найти координаты вершин полученной области. Здесь ясно прорисовались координаты только двух точек:
. Теперь нужно найти координаты вершин полученной области. Здесь ясно прорисовались координаты только двух точек:  . Остаётся решить вопрос с точками
. Остаётся решить вопрос с точками  .
.
Нетрудно заметить, что вершины  являются точками пересечением прямых. Найдём координаты вершины
являются точками пересечением прямых. Найдём координаты вершины 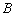 :
:

Примечание: из второго уравнения системы почленно вычтено первое уравнение.
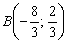
Найдём координаты точки  :
:
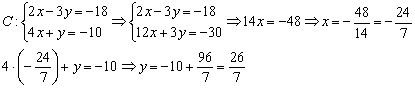
Примечание: второе уравнение системы умножено на 3, затем уравнения сложены почленно.

Для красоты координаты точек 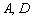 тоже можно найти аналитическим методом:
тоже можно найти аналитическим методом:

Ответ: область решений системы представляет собой многоугольник с вершинами в точках 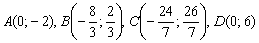 .
.
Задачи
1. Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.
2. Изобразите на координатной плоскости множество решений системы