
//код 6
[X,Y]=meshgrid(0:.2:1,0:.02:1);//meshgrid создаёт матрицы или трёхмерные массивы
Z=X.^2+Y.^2;//функция
xtitle('$\huge z=x^2+y^2$');//добавление заголовка в графическое окно
mesh(X,Y,Z);//mesh создает график трехмерной сетки

Рисунок 17 трехмерная сетка

Примечание: используйте функцию meshgrid() и mesh().
//код 7
[x,y]=meshgrid(-2:0.16:2,-2:0.16:2);//область определения х, у с шагами 0.16(т.к вариант- 16)
--> x0=0;
--> y0=0;
--> z=exp(-((x-x0).^2/2+(y-y0).^2/2));//функция
--> xtitle('$\huge z(x,y)=exp(-((x-x0).^2/2+(y-y0).^2/2))$');\
mesh(x,y,z);//реализация графика

Рисунок 18 сетчатый график функции

//код 8
[x,y]=meshgrid(-1:0.16:1,-1:0.16:1);//создание векторов
--> N=16;//номер варианта
--> z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция
--> mesh(x,y,z);//реализация графика

Рисунок 19 прозрачная сетчатая поверхность функции z(x,y)=N/2 sin(2πx) cos(1.5πy) (1-x^2)yx(1-y)
//к коду 8 приписываем следующие строчки
mesh_handle=get("hdl")//функция get позволяет получить текущий графический объект и
возвращает различные свойства, т.к. mesh имеет flag_color=0(белый или без цвета)
mesh_handle.color_mode=2//даем код цвета (синий)

Рисунок 20 непрозрачная сетчатая поверхность функции z(x,y)=N/2 sin(2πx) cos(1.5πy) (1-x^2)yx(1-y)
3.4. Постройте каркасную поверхность функции z (x y) с помощью команд
surf(X, Y, Z), surf(X, Y, Z, 'facecol','interp') и приведите их в отчете. Добавьте
также отображение сетки в трёхмерном пространстве.
//код 9
[x,y]=meshgrid(-1:0.16:1,-1:0.16:1);
N=16;//номер варанта
z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция графика
surf(x,y,z);//строит 3d графики
xgrid(2);//сетка

Рисунок 21 каркасная поверхность с помощью функции surf
//код 10
[x,y]=meshgrid(-1:0.16:1,-1:0.16:1);
N=16;//номер варанта
z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция графика
surf(x,y,z,'facecol','interp');//интерполированный режим затенения flag_color=3
xgrid(2);//сетка
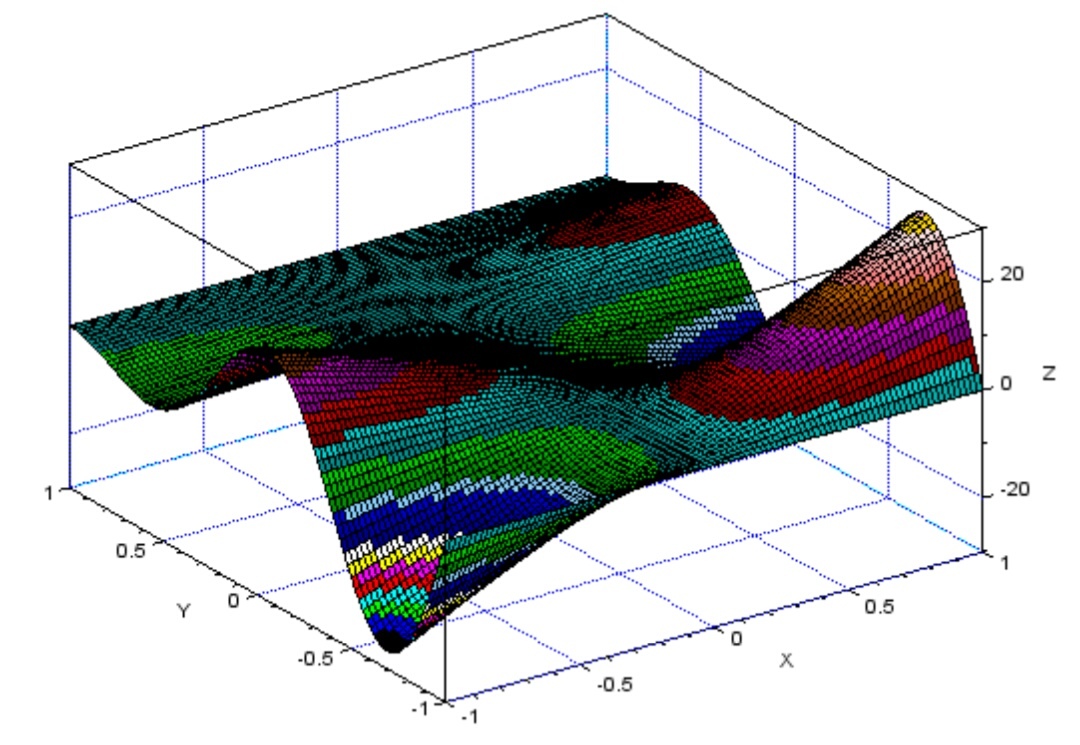
Рисунок 22 каркасная поверхность с помощью функции surf(x,y,z,'facecol','interp')
3.5. Постройте каркасную поверхность функции z= (x y с) помощью
следующего набора команд:
surf(X, Y, Z);
f = gcf();
f.color_map = hsvcolormap(32)
Результаты приведите в отчете и объясните что делает каждая строка.
--> surf(X, Y, Z) //строит каркасную поверхность
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = hsvcolormap(32)//изменяет насыщенность оттенка

Рисунок 23 каркасная поверхность (изменение насыщенности)
3.6. Постройте каркасную поверхность функции z (x y) с помощью команд
аналогичным выше со следующими палитрами: autumncolormap,
coolcolormap, pinkcolormap. Посмотрите, как будет меняться палитра при
изменении параметра n (например при числах 8, 16, 32).
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = autumncolormap (32)//цветовая карта от красного до
оранжевого, до желтого цвета. При изменении параметра n в большую
сторону палитра становится более четким(начинает приближаться к желтому
цвету)

Рисунок 24 поверхность с палитрой f.color_map = autumncolormap (32)

Рисунок 25 поверхность с палитрой f.color_map = autumncolormap (16)

Рисунок 26 поверхность с палитрой f.color_map = autumncolormap (8)
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = coolcolormap (32)//coolcolormap- вычисляет цветовую карту
с n цветами, варьирующимися от голубого до пурпурного. При изменении
параметра n в большую сторону палитра меняется, цвета распределяются
иначе.

Рисунок 27 поверхность с палитрой f.color_map = coolcolormap (32)

Рисунок 28 поверхность с палитрой f.color_map = coolcolormap (16)

Рисунок 29 поверхность с палитрой f.color_map = coolcolormap (8)
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = pinkcolormap (32)//pinkcolormap - раскрашивание цвета
сепии на черно-белые изображения. При изменении параметра n в большую
сторону палитра меняется, цвета начинают приближаться к белому

Рисунок 30 поверхность с палитрой f.color_map = pinkcolormap (32)

Рисунок 31 поверхность с палитрой f.color_map = pinkcolormap (16)

Рисунок 32 поверхность с палитрой f.color_map = pinkcolormap (8)
3.7. C помощью команды param3d(x,y,z) постройте параметрическую кривую
в объёмном пространстве, которая описывается следующим образом:

где параметр t - вектор, который должен изменяться от 0 до 10π. Шаг следует
выбирать в диапазоне от 0.001 до 0.01.
//код 11
t=[0:0.007:10*%pi];//вектор t в диапазоне [0,10π] и с шагом 0.007
--> clf
--> x=sin(t);//функция х
--> y=sin(t);//функция у
--> z=t;//функция z
--> param3d(x,y,z,theta=[2],alpha=[4]);//param3d-построение одной кривой в 3D декартовой рамке

Рисунок 33 реализация param3d