Содержание работы
Матрицы. Основные понятия.
Матрицей называется прямоугольная таблица чисел.
Пример 1.  ,
,  ,
, 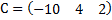 ,
,  .
.
В общем случае матрица может содержать 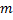 строк и
строк и  столбцов
столбцов
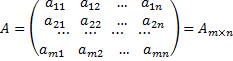 .
.
Числа  называются элементами матрицы, где
называются элементами матрицы, где  - указывает номер строки,
- указывает номер строки,  - указывает номер столбца.
- указывает номер столбца.
Элементы 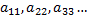 образуют главную диагональ матрицы.
образуют главную диагональ матрицы.
Если число строк равно числу столбцов, то матрица называется квадратной. Квадратная матрица размеров 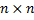 называется матрицей
называется матрицей  – го порядка.
– го порядка.
Квадратная матрица, у которой все элементы, кроме главной диагонали равны 0, называется диагональной.
Пример 2. 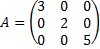 .
.
Если все элементы матрицы равны нулю, то матрица называется нулевой.
Пример 3.  .
.
Диагональная матрица, у которой каждый элемент диагонали равен 1, называется единичной.
Пример 4. 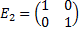 ,
, 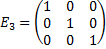 .
.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от диагонали, равны нулю.
Пример 5.  ,
, 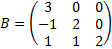 .
.
Матрица, содержащая одну строку (столбец), называется вектором (вектор-строкой, вектор-столбцом).
Пример 6.  ,
,  .
.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной 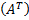 .
.
Пример 7. 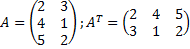 ;
;
Очевидно, что 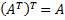 .
.
Действия над матрицами.
Матрицы одинаковых размерностей можно складывать и вычитать. Если
 ,
, 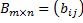 , то
, то 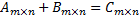 , причем
, причем
 , для всех
, для всех  .
.
Пример 8. 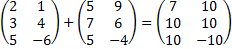 ,
,
 .
.
Умножение матрицы на число.
Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.
Пример 9. Пусть  , тогда
, тогда  .
.
Матрица 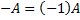 называется противоположной к матрице
называется противоположной к матрице 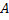 .
.
Умножение матриц.
Умножение матриц 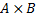 можно только в том случае, когда число столбцов матрицы
можно только в том случае, когда число столбцов матрицы 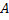 равно числу строк матрицы
равно числу строк матрицы 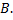 В этом случае справедливо соотношение
В этом случае справедливо соотношение 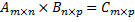 , причем элементы матрицы
, причем элементы матрицы 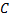 равны
равны  ,
, 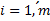 ,
,  .Другими словами строки матрицы
.Другими словами строки матрицы 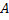 умножаются на столбцы матрицы
умножаются на столбцы матрицы 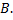
|
|
Пример 10. Пусть  ,
, 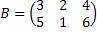 . Тогда
. Тогда
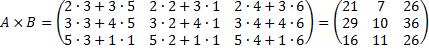 ,
,
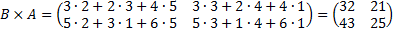 .
.
Видим, что в общем случае  . Если же выполняется условие
. Если же выполняется условие  , то матрицы
, то матрицы 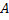 и
и 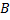 называются перестановочными друг с другом.
называются перестановочными друг с другом.
Определители.
Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.
Если 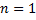 , то
, то 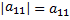 . Так
. Так 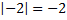 .
.
Если 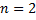 , то
, то 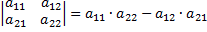 .
.
Так 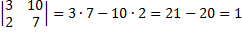 .
.
Если  , то
, то

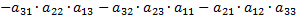 . Так
. Так
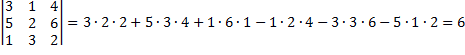 .
.
При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников. С плюсом берутся произведения элементов стоящих на главной диагонали и элементы, стоящие в вершинах следующих треугольников.

С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.

Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.

Вычисление определителей более высоких порядков осуществляется путем использования их свойств.
Из элементов этой матрицы можно составить определитель, который называется детерминантом матрицы 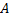 и обозначается
и обозначается
 Минором
Минором  некоторого элемента определителя
некоторого элемента определителя 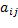 называют определитель, который получается вычеркиванием из него
называют определитель, который получается вычеркиванием из него 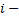 строки и
строки и  столбца. Например
столбца. Например
1. 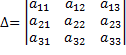 ,
, 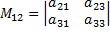 .
.
Алгебраическим дополнением элемента 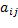 определителя называют число
определителя называют число  . Например
. Например
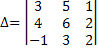 ,
,  .
.
Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например
|
|
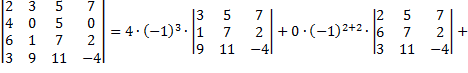
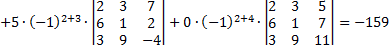 .
.
Задания для самостоятельного выполнения.
Задание №1.
| в а р и а н т | 1. Найти матрицу C=A+3B, если 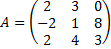 , , 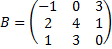 . .
| в а р и а н т | Найти матрицу C=A+2B, если 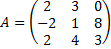 , , 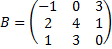
|
Задание №2. Вычислите определители матриц А и B, если:
| в а р и а н т |
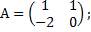
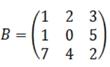
| в а р и а н т | 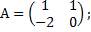
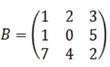
|