Оптика
Законы распр. света. Прицип Ферма. Полное внут отражение
Ко времени созд-я Максв. э/м теории уже были известны многие законом-ти распр. света. В проц-е набл-й и экспер-х исслед-й было устан-но, что всеет часто распр. в простр. в виде узких пучков – лучей света, направ-е кот-х ┴ фронту волны. Первыми оптич-ми зак-ми явились как раз зак-ны о распр. свет-х лучей, кот-е можно сформул-ть след-м образом:
1) З-н прямолин-го распр. света.
В однород-й изотроп-й среде луч света распр. по прямой.
2) З-н независимости световых лучей.
Свет-е лучи распр. в простр. незав-мо друг от друга. Пересеч-е лучей не влияет на характер их распр.
3) З-н отражения.
Луч падающий, отражённый и перпен-р к поверхности раздела двух сред, восстановл-й из точки падения луча, лежат в одной плос-и, назыв-й плоскостью падения. Угол пад-я α равен углу отраж-я β (рис. 1).
| V2<V1 |
| n2 |
| n1 |
| Рис.1 |
| γ |
| β |
| α |
4) З-н прелом-я.
Луч падающий, луч прелом-й и перпен-р к поверх-ти раздела двух сред, восстановл-й из точки падения луча, лежат в одной плос-ти – плос-ти падения. Отнош-е синуса угла падения α к син. угла прелом-я γ равно отнош-ю скоростей света в обеих средах (рис.1). Величина n12=V1/V2 наз. относит-м показ-м прелом-я среды 2 относ-но среды 1. Абсол-й показ-ль прелом-я – отнош-е скор-ти света в вакууме c к скор. света в среде V. n=c/V. => З-н прелом-я мож. зап-ть в виде: n1 sin α=n2 sin γ (1).
Полное внутреннее отражение.
если луч распр. из среды с большим показ-м прелом-я в среду с мень-м показ-м прелом-я (n1>n2), напр. из стекла в воду, то sin α/sin γ=n1/n2>1. => прелом-й луч удаляется от нормали и угол прелом-я γ больше угла падения α. С увеличением угла падения увелич-ся угол прелом-я, пока при некот-м предельном угле падения угол прелом-я не станет равным 900. При углах пад-я α>αпр весь падающий свет полностью отраж-ся. По мере приближ-я угла пад-я к предел-му интен-ть прелом-го луча уменьш., а отраж-го растёт. Т.о. при α=αпр интен-ть прелом-го луча=0, а интен-ть отраж-го =интен-ти пад-го. При углах пад-я от αпр до 900 луч не прелом-ся, а полностью отраж-ся в первую среду. Это явл-е полного внутр-го отраж-я. Предель-й угол мож. Найти из форм. (1), подставив αпр=900. => sin αпр=n2/n1=n21. Ур. удовл-ет знач-м угла αпр при n2≤n1. Явл. ПВО исп.в призмах полного отраж-я, рефрактометрах, световодах.
5) З-н обратимости свет-х лучей
Если луч света от А к В распр. по некотор-му пути АВ, то при распр. от В к А, во встречном направ., траектория распр. луча остаётся прежней.
Принцип Ферма.
Пытаясь описать опытные законом-ти поведения свет-х лучей с единых позиций, французский физик П.Ферма выдвинул принцип наим-го времени, гласящий: «Луч, распр-ся меж. двумя точками, идёт по пути, соответствующему экстремальному (чаще всего миним-му) времени.
Линзы. Оптические приборы: лупа, фотоап., проекц.фонарь
Линзы – прозрач-е тела, огранич-е двумя сферич-ми поверх-ми (в частном случае одна поверх-ть м.б. плоской), прелом-е свет-е лучи, способные формир-ть оптич-е изобр-я предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмасса и т.д. По внешней форме (рис. 1) линзы делятся на: 1) двояковып-е; 2) плосковып-е; 3) двояковогн-е; 4) плосковогн-е; 5) выпукло-вогн-е; 6) вогнуто-вып-е. По оптич-м свойствам линзы дел-ся на собирающие и рассеив-е.
| Рис. 1 |
Линза наз. тонкой, если расст-е меж. ограничив-ми повер-ми << радиусов этих поверх-й. Прямая через центры кривизны поверх-й линзы – главная оптич-я ось. Для всякой линзы сущ. точка, наз-я оптич-м центром линзы, леж-я на глав-й опт-й оси и облад-я тем свойством, что лучи походят сквозь неё не прелом-сь.
Формула линзы.
Это соотн-е связывает радиусы кривизны R1 и R2 поверх-й линзы с расст-ми a и b от линзы до предмета и его изображ-я. Восполь-ся принципом Ферма, или принц. наим-го времени: траект-я свет-го луча есть путь, для прохожд-я которого свету треб-ся миним-е время по срав-ю с любым другим путём между двумя теми же точками. Рассм. два свет-х луча (рис. 2) – луч, соед-й точки А и В (луч АОВ) и луч, проход-й через край линзы (луч АСВ). Восп-ся усл-м равенства прохож-я света вдоль АОВ и АСВ. Время прохож-я света вдоль АОВ: 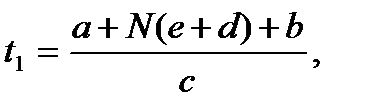 где N=n/n1 – относ-й показ-ть прел-я (n и n1 – соотв-но абсол-е показ-ли прел-я линзы и окруж-й среды). Время прох-я света вдоль АСВ равно:
где N=n/n1 – относ-й показ-ть прел-я (n и n1 – соотв-но абсол-е показ-ли прел-я линзы и окруж-й среды). Время прох-я света вдоль АСВ равно:  Т.к. t1=t2, то
Т.к. t1=t2, то 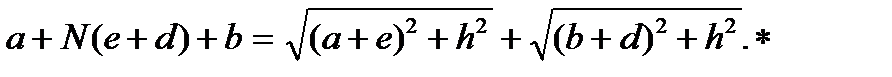
| b |
| a |
| B |
| d |
| e |
| h |
| R1 |
| A |
| R2 |
| C |
| Рис. 2 |
Рассм. параксиальные (приосевые) лучи, т.е. лучи, образ-е с опт-й осью малые углы. Т.о. все лучи паракс-го пучка из точки А перес-ют опт-ю ось в одной и той же точке В. Тогда h<<(a+e), h<<(b+d) и
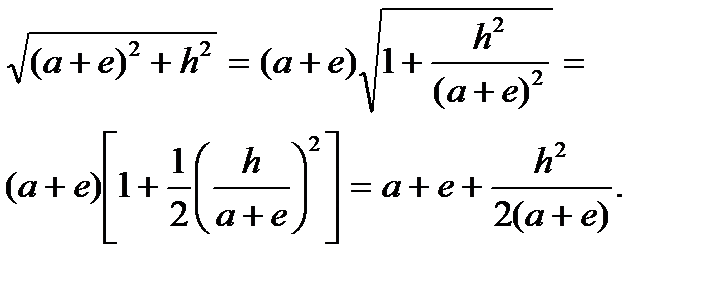
Анал-но, 
Подставив найд-е выраж-я в (*), получим 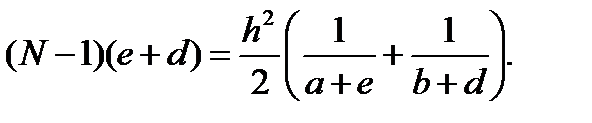
Для тонкой линзы e<<a и d<<b, => выраж-е мож. предст. в виде 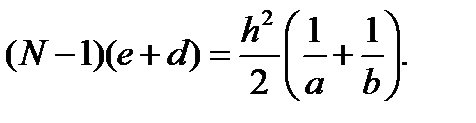
Т.к. 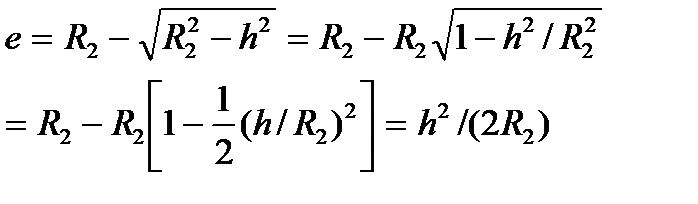 и соот-но d=h2/(2R1), получим
и соот-но d=h2/(2R1), получим 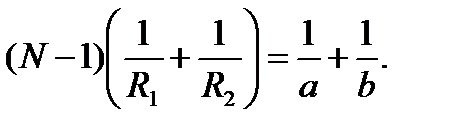
Это выр-е есть формула тонкой линзы. Радиус кривизны выпук-й поверх-ти счит. полож-м, вогн-й – отриц-м. Если а=∞, т.е. лучи падают на линзу парал-м пучком (рис. 3), то 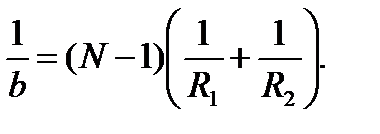
| f |
| F |
| Рис. 3 |
Расст. b=OF=f наз. фокусным расст-м линзы, опред-м по форм.: 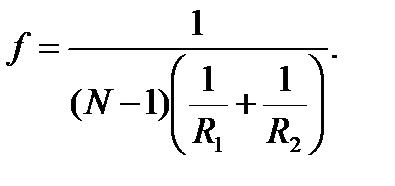
Если b=∞, т.е. изоб-е нах-ся в беск-ти и, след-но, лучи вых-т из линзы парал-м пучком, то a=OF=f. Т.о. фокус-е расст-я линзы, окружённой с обеих сторон одинак-й средой равны. Точки F, леж-е по обе стороны линзы на расст, равном фок-му, наз. фокусами линзы. Фокус – точка, в кот-й после прел-я собир-ся все лучи, пад-е на линзу парал-но глав-й опт-й оси. Величина 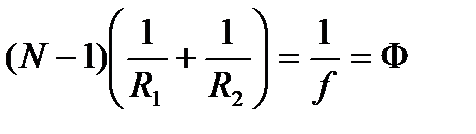
наз. опт-й силой линзы. Её единица – диоптрия (дптр). 1 дптр=1/м. Линза с полож-й опт-й силой – собирающая, с отриц. – рассеив-я. Плоскости, прох-е через фокусы линзы перпен-но её глав-й опт-й оси, наз. фокальными плоск-ми. Рассеив-я линза имеет мнимые фокусы. В мнимом фок-е сходятся воображаемые продолж-я лучей, падающ-х на расс-ю линзу парал-но гл. опт. оси.
Построение изобр-й в линзах.
Осущ-ся с пом-ю следующих лучей: 1) луча через опт-й центр (не меняющ-го своего направ-я); 2) луча, идущ. парал-но гл. опт. оси; после прелом-я в линзе этот луч (или его продолжение) прох-т через второй фокус линзы; 3) луча (или его продол-я), прох-го через первый фокус линзы; после прелом-я в ней он выходит из линзы парал-но её гл. опт. оси. Для примера на рис. 4 построено изобр-е в собир-й линзе (действит-е, оно перевёрн-е), а на рис. 5 в рассеив-й (мнимое, оно прямое). Отнош-е линейных размеров изобр-я и предмета – линейное увелич-е линзы.
| Рис. 4 |
| F |
| A| |
| F |
| B |
| A |
| B| |
Опт-е приборы.
Лупа. Простей-й опт-й прибор, представ-й собой выпук-е стекло с фокусным расст-м F, меньшим расст-я наилуч-го зрения L. Невооруж-й глаз видит предмет под углом зрения α0 (рис. 6). Поместив на пути лучей лупу и распол-я предмет в её фок-й плос-ти, получим учеличение угла зрения до знач. α. Угловое учелич-е есть  Лупа исп. также для увеличения освещ-ти действ-го изобр-я удалённых предметов. Простые выпу-е или плосковып-е лупы дают удовлет-е изобр-е при пяти-восьмикратном увеличении.
Лупа исп. также для увеличения освещ-ти действ-го изобр-я удалённых предметов. Простые выпу-е или плосковып-е лупы дают удовлет-е изобр-е при пяти-восьмикратном увеличении.
L
α0
F
α
Рис. 6
Фотоаппарат представ-т собой одну линзу, она должна создать качеств-е действ-е уменьш-е изобр-е на фотоплёнке. Линзы в соврем-х фотоап-х имеют фокус-е расст-я порядка неск-х см. т.е. << расст-й, на которые удалены объекты съёмки. Поэтому изобр-е получ-ся почти в фок-й плос-ти, его линей-е размеры пропорц-ны фок-му расст-ю F, а
F
F
B
A
A|
B|
Рис. 5
площадь – квадрату фок-го расст-я. Свет-й поток, проник-й в линзу фотоап-та, пропорц-н квадрату диаметра отверстия линзы D. У лучших объективов светосила (D/f)2 достигает значения 1÷1,5. Диафрагма ограничивает рабочее отверстие объектива и позволяет менять светосилу и глубину резкости.
Проекционный фонарь.
Явл-ся как бы обращённым фотоап-м, т.к. нужен для создания учелич-х изобр-й близких к фонарю объектов на удалённом экране. Требов-я к качеству изобр. менее строги, чем у фотоап-та, т.к. изобр-я рассм-ся зрителем на больших расст-х. Трудности: необходимость сильного освещ-я объекта и предохранения его от перегрева инфр-ми лучами от источника. Схема простей-го проек-го фонаря на рис. 7.
| 4FL |
| S |
| K |
| L |
| D |
| O |
| Э |
| Рис. 7 |
Свет-й поток от ист. S концентр-ся осветит-й линзой (часто это комбин-я из двуз плосковып-х линз), затем фокусир-ся на линзе О, создающей изобр-е диапозитива D, помещ-го сразу за освет-й линзой и пронизываемого всем свет-м потоком. При этом выгодно слева иметь симметр-й ход лучей, так что объект оказ-ся удалённым от линзы приблиз-но на удвоенное фок-е расст-е освет-й линзы. Т.к. экран распол-ся далеко, то увелич-е дел-ся значит-м. Меж. ист. света и освет-й линзой мож. поместить кювету с водой K, поглощ-й инфрак-е излуч-е.