Согласно волн-й теории свет – упругая волна, распр-ся в особой среде – эфире. Эфир заполняет всё мир-е простр-во, прониз-т все тела и облад-т мех-ми свойс-ми – упруг-ю и плот-ю. Волн-я теория основ-ся на принц. Гюйгенса: каждая точка, до кот. доходит волна служит центром вторич-х волн, а огибающая этих волн даёт полож-е волн-го фронта в след-й момент врем. Недост-ми волн-й теории явл., например, объяснение явл-й интерфер-и, дифр-и и поляриз-и только в случае, когда свет-е волны поперечные, невозм-ть объяснения физ-й природы наличия разных цветов.
Когерентность света – взаимная соглас-ть протек-я во врем. свет-х колеб-й в разных точках простр-а и (или) времени, характер-я их спос-ть к интерфер-и. В общем случ. свет.е колеб-я частично когер-ны и количественно их
когер-ть измер-ся степенью взаимной когер-ти, к-рая опред-т контраст интерфер-й картины в том или ином интерференц. экспер-те. Усл-ю когер-ти удовл-т монохроматичные волны – неогранич-е в простр-ве волны одной опред-й и строго пост-й частоты. Т.к. ни один реальный источ. не даёт строго монохром-го света, то волны от независ-х источ. света всегда некогер-ны. В двух самост-х источ. света атомы излуч. незав-мо друг от друга. Прерывистое изл-е света атомами в виде отдель-х коротких имп-в наз. волновым цугом. Любой немонохр-й свет мож. предст-ть в виде совокуп. Сменяющих друг друга незав-х гарм-х цугов. Средняя продолж-ть одного цуга τког наз. временем когер-ти. Когер-ть сущ. только в пределах одного цуга, и время когер-ти не мож. прев-ть время изл-я, т.е. τког<τ. Если волна распр. в однор-й среде, то фаза колеб-й в опред-й точке простр. сохр-ся только в теч-е времени τког. За это время волна распр. в вакууме на расст. l ког=сτког, наз-е длиной когер-ти (или длиной цуга). => набл-е интерфер-и света возм-но лишь при опт-х разностях хода, меньших длины когер-ти для используемого источ. света. Когер-ть колеб-й, кот. соверш-ся в одной и той же точке простр., определяемая степенью монохр-ти волн, наз. временнόй когер-ю. Два источ., размеры и взаимное распол-е кот. позв-т набл-ть интерфер-ю наз. пространственно-когер-ми. Радиусом когер-ти наз. макс-е поперечное направ-ю распр-я волны расст-е, на кот. возм-но проявл-е интер-и. Т.о. простр-я когер-ть опред-ся радиусом когер-ти rког=λ/φ, где λ – длина волны света, φ – угловой размер источ.
Интерфер-я света.
Пусть две монохр-е свет-е волны, наклад-сь друг на друга, возбуж-т в опред-й точке простр-ва колеб-я одинак-го направ: x1=A1cos(ωt+φ1) и x2=A2cos(ωt+φ2). Под х поним-т напряж-ть электр-го Е или магн-го Н полей волны, векторы Е и Н колеб-ся во взаимно перпен-х плос-х. Напряж-ти эл. и магн. полей подчин-ся принц. суперпоз-и. Амплитуда результир-го колеб-я в данной точке A2=A12+A22+2A1A2cos(φ2-φ1). Т.к. волны когер-ны, то cos(φ2-φ1) имеет пост-е во времени знач., поэт. интен-ть результир-й волны (I~A2) 
В точках простр., где cos(φ2-φ1)>0, интен-ть I>I1+I2, где cos(φ2-φ1)<0, I<I1+I2. => при налож-и двух (или неск-х) когер-х свет-х волн проис-т пространственное перераспред-е свет-го потока, в резуль. чего в одних местах возник-т макс-мы, а в других – мин-мы интен-ти. Это явл. наз. интерфер-й света. Для получ-я когер-х свет-х волн прим.т метод раздел-я волны от одного источ. на две части, кот-е после прохожд-я разныз опт-х путей наклад-ся друг на друга, и набл-ся интерфер-я картина. Пусть раздел-е волны проис-т в опред-й точке О. До точки М, в кот. набл-ся интер-я картина, одна волна в среде с показ-м прел-я n1 прошла путь s1, вторая – в среде с показ-м прел-я n2 – путь s2. Если в точке О фаза колеб-й равна ωt, то в точке М первая волна возб-т колеб-я A1cosω(t-s1/υ1), вторая волна – колеб-е A2cosω(t-s2/υ2), где υ1=c/n1, υ2=c/n2 – соот-но фазовая скор. первой и втор. волны. Разность фаз колеб-й, возб-х в точке М, равна
 (с учётом, что ω/c=2πν/c=2π/λ0, где λ0 – длина волны в вакууме). Произведение геометр-й длины пути s свет-й волны в данной среде на показ-ль прел-я n этой среды наз. опт-й длиной пути L, ∆=L2-L1 – разность опт-х длин проходимых волнами путей – наз. опт-й разностью хода. Если опт-я раз. хода равна целому числу длин волн в вакууме (*) ∆=±mλ0 (m=0, 1, 2,…), то δ=±2πm, и колеб-я, возбуждаемые в точке М обеими волнами, будут проис-ть в один-й фазе. След-но, (*) явл. усл-м интерфер-го макс-ма. Если опт-я раз. хода ∆=±(2m+1) λ0/2, то δ=±(2m+1)π, и колеб-я, возбуждаемые в точке М, будут проис-ть в противофазе. => это есть усл-е интер-го мин-ма.
(с учётом, что ω/c=2πν/c=2π/λ0, где λ0 – длина волны в вакууме). Произведение геометр-й длины пути s свет-й волны в данной среде на показ-ль прел-я n этой среды наз. опт-й длиной пути L, ∆=L2-L1 – разность опт-х длин проходимых волнами путей – наз. опт-й разностью хода. Если опт-я раз. хода равна целому числу длин волн в вакууме (*) ∆=±mλ0 (m=0, 1, 2,…), то δ=±2πm, и колеб-я, возбуждаемые в точке М обеими волнами, будут проис-ть в один-й фазе. След-но, (*) явл. усл-м интерфер-го макс-ма. Если опт-я раз. хода ∆=±(2m+1) λ0/2, то δ=±(2m+1)π, и колеб-я, возбуждаемые в точке М, будут проис-ть в противофазе. => это есть усл-е интер-го мин-ма.
Опыт Юнга.
Источ-м света служит ярко освещённая щель S (рис. 1), от кот. свет-я волна пад-т на две равноудалённые узкие щели S1 и S2, парал-е щели S. Т.о., щели S1 и S2 играют роль когер-х источ. Интер-я картина (область ВС) набл-ся на экране (Э), распол-м не некот-м расст. парал-но S1 и S2.
| S |
| S1 |
| S2 |
| B |
| C |
| Э |
| Рис. 1 |
Вопрос 4 Интерференция при отражении от тонких пластинок. Полосы равного наклона и равной толщины. Кольца Ньютона.
при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Это явление называется интерференцией света.
Для некогерентных волн разность ( ) непрерывно изменяется, поэтому среднее во времени значение cos(
) непрерывно изменяется, поэтому среднее во времени значение cos( ) равно нулю, а интенсивность результирующей волны всюду одинакова и при I1 = I2 равна 2I1 (для когерентных волн при данном условии в максимумах I= 4I1, в минимумах I= 0).
) равно нулю, а интенсивность результирующей волны всюду одинакова и при I1 = I2 равна 2I1 (для когерентных волн при данном условии в максимумах I= 4I1, в минимумах I= 0).
Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, па две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.
В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки.
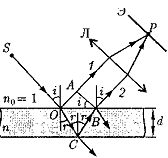

Полосы равного наклона (интерференция от плоскопараллельной пластины). Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
2. Полосы равной толщины (интерференция от пластинки переменной толщины).
Каждая из полос появляется при отражении от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произвольно). Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины.


Таким образом, полосы равной толщины локализованы вблизи поверхности клина. Если свет падает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.
3. Кольца Ньютона. Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с пей плосковыпуклой линзой с большим радиусом кривизны (рис.255). Параллельный пучок света надает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических колец. Центры колец Ньютона совпадают с точкой О соприкосновения линзы с пластинкой.

выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно:


Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны  . Поэтому система светлых в темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску.
. Поэтому система светлых в темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску.
Все рассуждения были проведены для отраженного света. Интерференцию
можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на  -, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.
-, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.