Свойства параллелепипеда

Содержание

Понятие призмы и виды призм

Понятие параллелепипеда

Свойства параллелепипеда

Дополнительные соотношения между элементами призмы

Задачи

Тесты

Глоссарий

Литература

 

Понятие призмы и виды призм

 

Рассмотрим два равных многоугольника и , расположенных в параллельных плоскостях и так, чтобы отрезки , соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

 

Рис. 1

 

 

Каждый из n четырехугольников

 

…, (1)

 

является параллелограммом, так как имеет попарно параллельные противоположные стороны.

Многогранник, составленный из двух равных многоугольников и , расположенных в параллельных плоскостях, и n параллелограммов (1), называется призмой.

Многоугольники и называются основаниями, а параллелограммы (1) – боковыми гранями призмы. Отрезки называются боковыми ребрами призмы. Эти ребра как противоположные стороны параллелограммов (1), следовательно приложенных друг к другу, равны и параллельны. Призму с основаниями и называют n – угольной призмой. На рисунке 2 изображены треугольная и шестиугольная призмы.

 

Рис. 2

 

 

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если ее основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники. На рисунке 2 изображена правильная шестиугольная призма. [1, 62]

 

Понятие параллелепипеда

 

Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы.

На рисунке 3 изображен наклонный параллелепипед, а на рисунке 4 – прямой параллелепипед.

 

	Рис. 3		Рис. 4

 

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. [4, 301]

Параллелепипед, боковые ребра которого перпендикулярны к плоскости основания, называется прямым параллелепипедом. У него все боковые грани прямоугольники, а основания параллелограммы. Если все грани параллелепипеда – прямоугольники, то его называют прямоугольным параллелепипедом. Длины трех его ребер, которые выходят из одной вершины, называются измерениями прямоугольного параллелепипеда.

Прямоугольный параллелепипед, все три измерения которого равны, называется кубом. Соотношение между различными видами параллелепипеда приведено в схеме: [2, 115]

 

 

Свойства параллелепипеда

Теорема:

У параллелепипеда:

1) противолежащие грани равны и параллельны;

2) все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Доказательство:

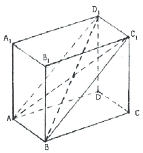
1) Рассмотрим какие-нибудь две противоположные грани параллелепипеда, например, и (рис. 5).

 

	Рис. 5

 

 

Поскольку все грани параллелепипеда – параллелограммы, то прямая AD параллельна прямой ВС, а прямая параллельна прямой . Отсюда следует, что плоскости рассматриваемых граней параллельны.

Из того, что грани параллелепипеда – параллелограммы, следует, что АВ, , CD и параллельны и равны. Отсюда сделаем вывод, что грань совмещается параллельным переносом вдоль ребра АВ с гранью . Следовательно, эти грани равны.

2) Возьмем две диагонали параллелепипеда (рис. 5), например, и , и проведем дополнительные прямые и . АВ и соответственно равны и параллельны ребру DC, поэтому они равны и параллельны между собою; вследствии этого фигура есть параллелограмм, в котором прямые и – диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам. Аналогично мы можем доказать, что две другие диагонали пересекаются в одной точке и делятся этой точкой пополам. Точка пересечения каждой пары диагоналей лежит в середине диагонали . Таким образом, все четыре диагонали параллелепипеда пересекаются в одной точке О и делятся этой точкой пополам. Таким образом, точка пересечения диагоналей параллелепипеда является его центром симметрии. [3, 21]

Теорема:

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Доказательство:

Это выплывает из пространственной теоремы Пифагора. Если – диагональ прямоугольного параллелепипеда , то – ее проекции на три попарно перпендикулярные прямые (рис. 6). Следовательно, . [2, 116]

 

	Рис. 6

Замечание: в прямоугольном параллелепипеде все диагонали равны.