Если в наклонной призме боковое ребро  образует одинаковые углы со сторонами основания, которые выходят из вершины
образует одинаковые углы со сторонами основания, которые выходят из вершины  , то основание О высоты
, то основание О высоты  лежит на биссектрисе угла
лежит на биссектрисе угла  (рис. 7).
(рис. 7).
Доказательство: 
|

Проведем 
 и отрезки
и отрезки 
 Согласно теореме о трех перпендикулярах, имеем
Согласно теореме о трех перпендикулярах, имеем  и
и  . Прямоугольные треугольники
. Прямоугольные треугольники 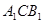 и
и  равны, поскольку имеют общую гипотенузу
равны, поскольку имеют общую гипотенузу  и одинаковые углы (
и одинаковые углы ( по условию). Следовательно,
по условию). Следовательно,  и
и  , отсюда
, отсюда  Таким образом, точка О равноудалена от сторон угла
Таким образом, точка О равноудалена от сторон угла  и, следовательно, лежит на биссектрисе
и, следовательно, лежит на биссектрисе  угла
угла  . [3, 24]
. [3, 24]
Задачи
1. Ребро куба равно а.
Найдите:
Диагональ грани: d= a√2.
Диагональ куба: D= a√3.
Периметр основания: P= 4a.

2. Основанием прямой призмы является равнобедренный треугольник, в котором высота проведенная к основанию равняется 8см. Высота призмы равняется 12см. Найдите полною поверхность призмы если боковая грань что содержит основание треугольника - квадрат.

Решение
Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть  , где
, где  - площадь основания призмы,
- площадь основания призмы,  - площадь боковой поверхности, содержащей основание,
- площадь боковой поверхности, содержащей основание,  - площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)
- площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)
Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см. (основание треугольника одновременно является стороной грани).
Таким образом, зная высоту и основание равнобедренного треугольника можно найти его остальные стороны и площадь:

Катеты, соответственно равны (у нас высота, являющаяся в равнобедренном треугольнике одновременно и медианой  , с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора:
, с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора:

Таким образом:
 ,
, 

3. В правильной четырёхугольной призме площадь основания 144  , а высота 14 см. Найти диагональ призмы.
, а высота 14 см. Найти диагональ призмы.
Решение
Правильный четырехугольник – это квадрат.
Соответственно, сторона основания будет равна 
Откуда диагональ основания правильной прямоугольной призмы будет равна 
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна: 
Ответ: 22 см
4. Рассмотрим правильную четырехугольную призму 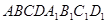 , диагональное сечение которой – квадрат. Через вершину
, диагональное сечение которой – квадрат. Через вершину  и середины ребер АВ и ВС проведена плоскость. Найти площадь полученного сечения, если
и середины ребер АВ и ВС проведена плоскость. Найти площадь полученного сечения, если 
Решение

Построение сечения видно на рисунке, где К и L – середины сторон АВ и ВС основания призмы, Е и F – точки пересечения прямой КL соответственно с продолжениями сторон DA и DC. Сечением является пятиугольник  площадь которого можно найти. Можносначала вычислить площади треугольников
площадь которого можно найти. Можносначала вычислить площади треугольников  и
и  а потом от площади первого треугольника вычесть удвоенную площадь второго (поскольку треугольники
а потом от площади первого треугольника вычесть удвоенную площадь второго (поскольку треугольники  и
и  равны). Однако в данном случае проще воспользоваться формулой:
равны). Однако в данном случае проще воспользоваться формулой:

Проекция пятиугольника  на плоскость основания призмы есть пятиугольник
на плоскость основания призмы есть пятиугольник  , площадь которого найдем, вычитая из площади квадрата
, площадь которого найдем, вычитая из площади квадрата  площадь треугольника ВКL:
площадь треугольника ВКL:

Пусть диагональ ВD основания пересекает отрезок КL в точке О. Так как  и
и  (согласно теореме о трех перпендикулярах), то
(согласно теореме о трех перпендикулярах), то  – линейный угол двугранного угла КL.
– линейный угол двугранного угла КL.
Далее находим:


Из прямоугольного треугольника  по теореме Пифагора имеем:
по теореме Пифагора имеем:
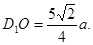
Значит,  и
и 
5. Дана правильная призма:  ,
,  . Найти высоту призмы.
. Найти высоту призмы.
Решение

Площадь основания 
АВ= 2 см.
Периметр основания Р = 8 см.
Высота призмы 
6. Основанием параллелепипеда служит квадрат. Одна из вершин верхнего основания равноудалена от всех вершин нижнего основания и находится на расстоянии b от этого основания. Сторона основания равна a. Найдите полную поверхность параллелепипеда.
Решение
Пусть  – данный параллелепипед с основаниями
– данный параллелепипед с основаниями  ,
,  и боковыми рёбрами
и боковыми рёбрами  , причём ABCD – квадрат со стороной a, вершина
, причём ABCD – квадрат со стороной a, вершина  равноудалена от вершин A, B, C и D, а расстояние от вершины
равноудалена от вершин A, B, C и D, а расстояние от вершины  до плоскости основания ABCD равно b. Поскольку точка
до плоскости основания ABCD равно b. Поскольку точка  равноудалена от вершин квадрата ABCD, она лежит на перпендикуляре к плоскости ABCD, проходящем через центр O квадрата. Перпендикуляр, опущенный из точки O на сторону BC, проходит через её середину M. По теореме о трёх перпендикулярах
равноудалена от вершин квадрата ABCD, она лежит на перпендикуляре к плоскости ABCD, проходящем через центр O квадрата. Перпендикуляр, опущенный из точки O на сторону BC, проходит через её середину M. По теореме о трёх перпендикулярах 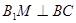 , поэтому
, поэтому  – высота грани
– высота грани  . Из прямоугольного треугольника
. Из прямоугольного треугольника  находим, что
находим, что
 .
.
Значит,

Аналогично,

Если S – полная поверхность параллелепипеда  , то
, то
 .
.
7. Докажите, что если сечение параллелепипеда плоскостью является многоугольником с числом сторон, большим трёх, то у этого многоугольника есть параллельные стороны.
Доказательство
У параллелепипеда 3 пары параллельных граней. Если плоскость пересекает более трёх граней, то по крайней мере две стороны многоугольника сечения лежат в противоположных гранях параллелепипеда. По теореме о пересечении двух параллельных плоскостей третьей эти две стороны параллельны.
8. В параллелепипеде  грань ABCD – квадрат со стороной 5, ребро
грань ABCD – квадрат со стороной 5, ребро  также равно 5, и это ребро образует с рёбрами AB и AD углы
также равно 5, и это ребро образует с рёбрами AB и AD углы  . Найдите диагональ
. Найдите диагональ  .
.
Решение
Треугольник  – равносторонний, т.к.
– равносторонний, т.к.  = AB и
= AB и  . Поэтому
. Поэтому  . Аналогично,
. Аналогично,  . Боковые рёбра
. Боковые рёбра  треугольной пирамиды
треугольной пирамиды  с вершиной
с вершиной  равны между собой, значит, высота
равны между собой, значит, высота  этой пирамиды проходит через центр окружности, описанной около основания ABD, а т.к. треугольник ABD прямоугольный, то точка O – середина его гипотенузы BD, т.е. центр квадрата ABCD. Из прямоугольного треугольника
этой пирамиды проходит через центр окружности, описанной около основания ABD, а т.к. треугольник ABD прямоугольный, то точка O – середина его гипотенузы BD, т.е. центр квадрата ABCD. Из прямоугольного треугольника  находим, что
находим, что

Поскольку  , точка
, точка  равноудалена от вершин C и D, поэтому её ортогональная проекция K на плоскость основания ABCD также равноудалена от C и D, а значит, лежит на серединном перпендикуляре к отрезку CD. Поскольку
равноудалена от вершин C и D, поэтому её ортогональная проекция K на плоскость основания ABCD также равноудалена от C и D, а значит, лежит на серединном перпендикуляре к отрезку CD. Поскольку  ||
||  и
и  =
=  , четырёхугольник
, четырёхугольник  – прямоугольник, поэтому OK=
– прямоугольник, поэтому OK=  =5. Продолжим отрезок KO до пересечения с отрезком AB в точке M. Тогда M – середина AB и MK=MO+OK=
=5. Продолжим отрезок KO до пересечения с отрезком AB в точке M. Тогда M – середина AB и MK=MO+OK=  . Из прямоугольных треугольников MKB и
. Из прямоугольных треугольников MKB и  находим, что:
находим, что:

9. На ребре AD и диагонали  параллелепипеда
параллелепипеда  взяты соответственно точки M и N, причём прямая MN параллельна плоскости
взяты соответственно точки M и N, причём прямая MN параллельна плоскости  и AM:AD = 1:5. Найдите отношение
и AM:AD = 1:5. Найдите отношение  .
.
Решение
Пусть P – центр параллелограмма ABCD. Плоскости  и
и  пересекаются по прямой
пересекаются по прямой  , поэтому прямые
, поэтому прямые  и
и  пересекаются в некоторой точке Q, причём
пересекаются в некоторой точке Q, причём

По теореме о пересечении двух параллельных плоскостей третьей плоскости α и  пересекаются по прямой, проходящей через точку E параллельно
пересекаются по прямой, проходящей через точку E параллельно  . Ясно, что точка пересечения этой прямой с прямой
. Ясно, что точка пересечения этой прямой с прямой  и есть точка N (прямая MN лежит в плоскости, параллельной плоскости
и есть точка N (прямая MN лежит в плоскости, параллельной плоскости  ). Рассмотрим параллелограмм
). Рассмотрим параллелограмм  . Так как
. Так как
 то
то 

10. Три отрезка, не лежащие в одной плоскости, имеют общую точку и делятся этой точкой пополам. Докажите, что концы этих отрезков служат вершинами параллелепипеда.
Решение
Пусть O – общая середина отрезков  ,
,  и
и  . Тогда AB||
. Тогда AB||  и AD||
и AD||  . Значит, плоскости ABD и
. Значит, плоскости ABD и 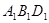 параллельны. Аналогично, плоскость
параллельны. Аналогично, плоскость  параллельна плоскости
параллельна плоскости  . В плоскостях ABD и
. В плоскостях ABD и 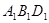 возьмём соответственно точки C и
возьмём соответственно точки C и  так, что ABCD и
так, что ABCD и  – параллелограммы. Так как CD||AB, AB||
– параллелограммы. Так как CD||AB, AB||  и
и  ||
||  , то CD||
, то CD||  . Поэтому плоскости
. Поэтому плоскости  и
и  также параллельны. Шестигранник
также параллельны. Шестигранник  , образован пересечением трёх пар параллельных плоскостей. Следовательно, это параллелепипед.
, образован пересечением трёх пар параллельных плоскостей. Следовательно, это параллелепипед.
Тесты
1. Найдите длину диагонали прямоугольного параллелепипеда, измерения которого равны 2 см, 3 см и 4 см.
Варианты ответов:
| А | Б | В | Г | Д |
 см см
| 9 см |  см см
| 24 см |  см см
|
Решение
Длина диагонали параллелепипеда равна корню из суммы квадратов его измерений и составит 
2. Сосчитайте сколько у прямоугольного параллелепипеда рёбер
Варианты ответов:
| А | Б | В | Г | Д |
3. Многогранник, составленный из двух равных многоугольников  и
и  , расположенных в параллельных плоскостях, и n параллелограммов
, расположенных в параллельных плоскостях, и n параллелограммов 
 …,
…,  , называется:
, называется:
А) параллелепипед;
Б) призма;
В) пирамида;
Г) многогранник;
Д) конус.
4. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется…
А) высотой призмы;
Б) ребром призмы;
В) медианой призмы;
Г) диагональю призмы;
Д) стороной призмы.
5. Прямая призма называется правильной, если ее основания…
А) равнобедренные треугольники;
Б) не правильные многоугольники;
В) параллелограммы;
Г) окружности;
Д) правильные многоугольники.
6. У параллелепипеда все грани...
А) параллелограммы;
Б) треугольники;
В) трапеции;
Г) шестиугольники;
Д) квадраты.
7. В прямоугольном параллелепипеде все ли диагонали равны?
А) нет;
Б) да.
8. У параллелепипеда противолежащие грани равны и …
А) параллельны;
Б) лежат в одной плоскости;
В) перпендикулярны;
Г) лежат в разных плоскостях;
Д) образуют между собой угол 
9. У параллелепипеда все четыре диагонали пересекаются в одной точке и делятся в ней …
А) в отношении 1:2;
Б) в отношении 1:3;
В) пополам;
Г) в отношении 1:5;
10. Чему равен квадрат диагонали прямоугольного параллелепипеда?
А) сумме квадратов трех его измерений;
Б) сумме ребер;
В) сумме трех его измерений;
Г) сумме квадратов ребер;
Д) корню из суммы трех его измерений.
Глоссарий
Ø Многогранник, составленный из двух равных многоугольников  и
и  , расположенных в параллельных плоскостях, и n параллелограммов
, расположенных в параллельных плоскостях, и n параллелограммов 
 …,
…,  , называется призмой.
, называется призмой.

Ø Многоугольники  и
и  называются основаниями, а параллелограммы
называются основаниями, а параллелограммы 
 …,
…,  – боковыми гранями.
– боковыми гранями.
Ø Призму с основаниями  и
и  называют n – угольной призмой.
называют n – угольной призмой.
Ø Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Ø Прямая призма называется правильной, если ее основания – правильные многоугольники.
Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы.
Ø Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Ø Параллелепипед, боковые ребра которого перпендикулярны к плоскости основания, называется прямым параллелепипедом.
Ø У параллелепипеда все боковые грани прямоугольники, а основания параллелограммы. Если все грани параллелепипеда – прямоугольники, то его называют прямоугольным параллелепипедом.
Ø Длины трех его ребер, которые выходят из одной вершины, называются измерениями прямоугольного параллелепипеда.
Ø Прямоугольный параллелепипед, все три измерения которого равны, называется кубом.
Литература
1. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Учеб. для 10 – 11 кл. сред. шк. – М.: Просвещение, 1992 – 207с.
2. Геометрія: Підруч. для учнів 10 – 11 кл. з поглибл. вивч. математики в серед. загально-освіт. закладах /Г. П. Бевз, В. Г. Бевз, В. М. Владіміров, Н. Г. Владімірова. – 2-ге вид. – К.: Освіта, 2003. – 239 с.
3. Лосєва Н. М. Геометричні тіла: Навчальний посібник. – Донецьк: ДонНУ, 2006. – 240 с.
4. Погорелов А. В. Геометрия: Учеб. для 7 – 11 кл. общеобразоват. учреждений. – 5-е изд. – М.: Просвещение, 1995. – 383 с.