ферромагнитных материалов

 

Закон полного тока гласит: интеграл от напряженности магнитного поля по любому замкнутому контуру равен алгебраической сумме токов, сцепленных с этим контуром:

 

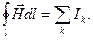(3.3)

Установлен закон полного тока опытным путем.

В случае, когда контур интегрирования охватывает w витков катушки с током I, получим другую запись аналитического выражения (3.3)

Таким образом

 

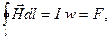(3.4)

где F = I∙w – магнитодвижущая сила (МДС) аналог ЭДС. Измеряется F в амперах (А) или в ампер-витках (А∙в).

На основании закона полного тока получают закон Ома для магнитной цепи

 

Ф = F / r_M, (3.5)

 

где F – МДС; r_M = l_CP /(μ_а S) – магнитное сопротивление участка цепи, 1/Гн; l_CP - длина средней линии магнитной индукции В м;

S – поперечное сечение участка магнитной цепи, м².

 

Петля гистерезиса

Однако закон (3.5) в большинстве случаев применим с ограничениями, так как зависимость B = f(H), не является линейной. Для ферромагнитных материалов абсолютная магнитная проницаемость μ_а зависит от напряженности магнитного поля Н.

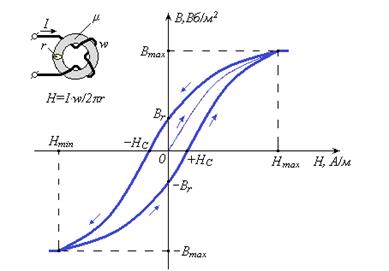
Зависимость B = f(H), называемая петлей гистерезиса, приведена на рисунке 3.2. Ее получают экспериментальным путем на образце ферромагнитного материала, в котором магнитное поле однородно, например – тороид с намотанной катушкой, в которой может протекать ток требуемой величины. Не вдаваясь во все тонкости эксперимента, проанализируем полученную зависимость.

В первоначальный момент, до появления тока I в катушке, напряженность магнитного поля H = 0 и магнитная индукция В = 0. При появлении тока в катушке и его увеличении появится и будет возрастать напряженность магнитного поля H и будет увеличиваться значение магнитной индукции В = f(H) (см. рис. 3.2, тонкая линия). Это графическая зависимость первоначального намагничивания образца ферромагнитного материала. Она нелинейная. Достигнув при некотором значении напряженности магнитного поля H_max значения B = В_max, магнитная индукция перестает увеличиваться. Наступает насыщение.

Рис. 3.2 – Статическая петля гистерезиса

Если, достигнув насыщения, плавно, уменьшая ток I в катушке, уменьшать напряженность магнитного поля H, то магнитная индукция также будет уменьшаться. Но зависимость В = f(H) на обратном ходе не будет совпадать с зависимостью первоначального намагничивания (Рис. 3.2, жирная линия).

При токе I = 0 и H = 0 магнитная индукция В ≠ 0 будет иметь значение В = B_r. Величина B_r называется остаточной магнитной индукцией. Нулевое значение магнитной индукции получим при отрицательном токе, когда H = – H_С. Значение H_С называется коэрцетивной силой. Дальнейшее увеличение отрицательных значений напряженности H снова приводит к насыщению ферромагнитного материала, когда при H ≤ H_min магнитная индукция В будет равной – В_max. Если теперь изменять значение напряженности H от отрицательных, проходя точки H = H_min, H = 0 и H = H_max, то получим новую ветвь зависимости B = f(H), расположенную ниже первых двух (Рис. 3.2). На ней также будут расположены характерные точки с координатами (0; –В_max) и (+ H_С; 0). В результате нескольких циклов такого перемагничивания получается симметричная фигура, ограниченная жирной линией, которую и называют предельной статической петлей гистерезиса или просто – петлей гистерезиса.

Коэрцетивная сила H_С, остаточная магнитная индукция B_r и коэффициент прямоугольности k_□ = B_r / В_max характеризуют предельный статический цикл гистерезиса ферромагнитного материала.

По значению параметра H_С ферромагнитные материалы различают как магнитно-мягкие (H_С < 0,01 А/м) и магнитно-твердые (H_С > 20…30 кА/м).

Магнитно-твердые материалы обладают способностью сохранять высокие значения остаточной магнитной индукции после устранения действия намагничивающего поля. К ним относятся литые и порошковые сплавы, включающие железо, никель, кобальт, ванадий, алюминий и другие элементы, а также ферриты. Магнитно-твердые материалы используются для изготовления постоянных магнитов.

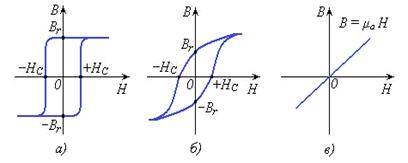
Магнитно-мягкие материалы делятся на три типа: магнитные материалы с прямоугольной петлей гистерезиса (k_□ > 0,95); магнитные материалы с округлой петлей гистерезиса (0,4< k_□ < 0,7); магнитные материалы с линейными свойствами, у которых зависимость B = f(H) практически линейная (Рис. 3.3).

 

 

Рис. 3.3 – Типы характеристик магнитно-мягких материалов: а) прямоугольная; б) округлая; с) линейная

К таким материалам относятся различные марки пермаллоя, перминвар, ферриты с низкими значениями B_r и H_С, аморфные материалы (металлические стекла) и другие.

Магнитно-мягкие материалы используются для изготовления сердечников и магнитопроводов электрических машин и аппаратов, в устройствах автоматики, в радиоэлектронике и в других областях техники.

 

Неразветвленные и разветвленные магнитные цепи

Задачей расчета неразветвленной магнитной цепи чаще всего является определение МДС F = I∙w (3.4), необходимой для вычисления тока в катушке I, магнитного потока Ф или магнитной индукции В в некотором сечении S_К магнитопровода.

Учитывая, что магнитный поток во всей неразветвленной цепи одинаков, значение магнитной индукции в к -ом сечении

 

В_К = Ф / S_К = μ_аК Н_К. (3.6)

 

Из (3.6), с учетом (10.5) получим:

 

Н_К = В_К / μ_а и далее . (3.7)

 

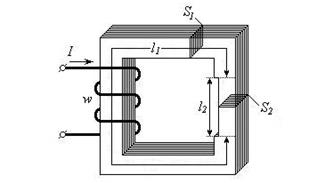
Рассмотрим схему магнитной цепи, состоящую из магнитопровода с катушкой (Рис. 3.4), для которой магнитный поток Ф известен. Требуется определить величину тока I в катушке с количеством витков w, необходимую для создания требуемого магнитного потока. Цепь состоит из двух участков, геометрические параметры которых l₁, S₁ и l₂ , S₂ (l - длина участка, S – поперечное сечение участка). Магнитные свойства материала заданы зависимостью В = μ_а Н.

Если магнитный поток Ф задан, то он будет одинаковым для любого сечения магнитопровода

Ф = В₁ S₁ = В₂ S₂.

 

Тогда согласно формуле (3.7)

, (3.8)

 

где Н₁ и Н₂ напряженности магнитного поля в первом и втором участках магнитопровода.

Рис. 3.4 – Простая магнитная цепь

Согласно закону Ома (3.5) для заданной магнитной цепи

Ф = F /(r_{M 1} + r_{M 2}). Тогда, с учетом (3.8), получим искомый ток

 

(3.9)

 

где r_M1 = l₁ / S₁ μ_а - магнитное сопротивление участка длиной l₁;

r_{M 2} = l₂ / S₂ μ_а - магнитное сопротивление участка длиной l₂.

В этих соотношениях μ_а = μ_а (Н), то есть является нелинейной величиной.

Обратная задача, когда требуется при известной МДС F определить магнитный поток Ф, сложнее. Решение можно получить графическим путем, используя магнитную характеристику цепи F = f(Ф).

В разветвленной магнитной цепи (например, изображенной на рис. 3.1, б) могут существовать несколько магнитных потоков, которые на определенных участках могут складываться или вычитаться. Здесь используются аналогии с первым и вторым законами Кирхгофа.

Первый закон Кирхгофа для магнитной цепи гласит: в любом узле разветвленной магнитной цепи алгебраическая сумма магнитных потоков равна нулю:

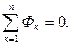(3.10)

 

Второй закон Кирхгофа для магнитной цепи формулируется так: в любом контуре магнитной цепи алгебраическая сумма магнитодвижущих сил равна алгебраической сумме призведений магнитных потоков в ветвях данного контура и магнитных сопротивлений этих ветвей:

 

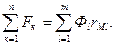(3.11)

 

Катушка индуктивности в цепи переменного тока

В цепях переменного тока часто используются катушки индуктивности с сердечниками и с магнитопроводами из ферромагнитных материалов. При расчете электрических цепей, содержащих такие элементы, возникает потребность в схемах их замещения, позволяющих упростить расчет.

Рассмотрим катушку индуктивности с магнитопроводом, имеющую w витков провода с сопротивлением R_к (Рис. 3.5, а). За счет тока i катушки в магнитопроводе будет формироваться магнитный поток Ф – как основной, и магнитный поток рассеяния, характеризуемый потокосцеплением Ψ_рас.

Потокосцепление рассеяния Ψ_рас зависит от конструкции катушки и, практически, не зависит от магнитопровода. Магнитные силовые линии потока рассеяния замыкаются, в основном, по воздуху и только частично проходят по магнитопроводу.

В воздухе магнитная индукция В = μ₀ Н, где μ₀ - постоянная величина. Поэтому можно считать, что потокосцепление и ток будут связаны линейной зависимостью:

 

Ψ_рас = L_расi, (3.12)

 

где L_рас – индуктивность рассеяния обмотки.

Рис. 3.5 –Катушка индуктивности в цепи переменного тока: а) катушка индуктивности с магнитопроводом; б) схема замещения катушки с магнитопроводом

Потокосцепление основного магнитного потока равно wФ. Тогда полное потокосцепление для рассматриваемой катушки

 

Ψ = w Ф + Ψ_рас. (3.13)

 

С учетом активного сопротивления катушки R_к и потоко-сцепления Ψ (3.13) напряжение u на зажимах катушки

 

u = R_к i + 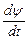= 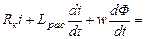u_R + u_Lpac + u₀. (3.14)

 

Из (3.14) следует, что катушку с ферромагнитным сердечником можно представить в виде последовательно соединенных активного сопротивления R_к, индуктивного элемента L_рас и идеальной катушки индуктивности с индуктивностью L₀, которая не имеет индуктивности рассеяния (Рис. 3.5, б). Физически идеальную катушку индуктивности можно представить в виде катушки с ферромагнитным сердечником, заключенной в ферромагнитный экран, за пределы которого магнитное поле не проникает.

 

Для идеальной катушки индуктивности

 

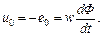(3.15)

 

Получим для идеальной катушки индуктивности закон изменения магнитного потока Ф. Пусть напряжение u₀. = U_0m sin ωt. Подставив u₀ в (3.15), получим:

 

dФ = 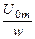sin ωt dt. (3.16)

 

Проинтегрировав (3.16), получим:

 

Ф = 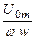sin (ωt + π/2) + А.

 

Для переменного тока постоянная интегрирования А = 0. Тогда

 

Ф = 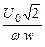sin (ωt + π/2), (3.17)

 

где U₀ – действующее значение напряжения u₀.

Амплитудное значение магнитного потока

 

Ф_m 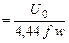. (3.18)

 

В выражении (3.18) f – циклическая частота. Сомножитель в знаменателе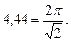

Если задан магнитный поток Ф, то действующее значение напряжения u₀ можно найти как

 

U₀ = Е₀ = 4,44 f w Ф_т. (3.18)

Выражение (3.18) удобно для расчета ЭДС, индуктируемых в обмотках трансформаторов и других электрических машин.

Схема замещения катушки индуктивности с магнитопроводом в цепи переменного тока, приведенная на рис. 3.2, б, не учитывает потерь энергии магнитного поля на гистерезис (перемагничивание) материала магнитопровода.

Если воспользоваться законом Ома в комплесной форме и определить комплексное сопротивление идеализированной катушки, то получим:

 

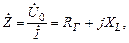(3.19)

 

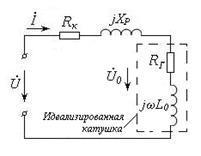
где R_Г – активное сопротивление, учитывающее потери электрической энергии на гистерезис; X_L = jωL₀ – индуктивное сопротивлениеидеализированной катушки (Рис.3.6).

Рис.3.6 – Схема замещения катушки индуктивности с магнитопроводом

3.3 Общие сведения о трансформаторах

 

Трансформатором называется электромагнитное устройство, предназначенное для преобразования (трансформации) одного напряжения в другое напряжение той же частоты. Трансформаторы используют для получения различных уровней напряжения на производстве и в быту, а также в системах передачи и распределения электроэнергии. Их применение обеспечивает экономичную передачу электроэнергии к потребителям. Передача электроэнергии ведется при повышенном напряжении, что позволяет уменьшить сечение проводов линий электропередач и потери мощности в них.

Трансформатор содержит две обмотки, или большее количество, и магнитопровод (Рис. 3.7). Обмотка, подключенная к источнику, называется первичной. Обмотка, к которой подключается нагрузка (на рис 3.7 сопротивление Z_H), является вторичной. Магнитопровод необходим в трансформаторе для усиления электромагнитной связи между обмотками. Для уменьшения вихревых токов в магнитопроводе и снижения потерь энергии на его нагрев, магнитопровод набирают из тонких листов электротехнической стали.

 

Рис. 3.7 – Трансформатор

Существуют однофазные и трехфазные трансформаторы. Однофазные (Рис. 3.7) используются в однофазных сетях переменного тока. Трехфазные трансформаторы (Рис. 3.8) предназначены для работы в трехфазных сетях. Они содержат, как минимум, три пары обмоток, из которых три первичные и три вторичные. Для первичных обмоток используют обозначения в виде заглавных букв, как показано на рисунке 3.8. Вторичные обмотки обозначают прописными буквами.

Трансформаторы могут быть повышающими и понижа-ющими. У понижающего трансформатора число витков первичной обмотки больше, чем вторичной, и напряжение первичной обмотки больше, чем вторичной, то есть w₁>w₂ и U₁>U₂. Если w₂>w₁ и U₂>U₁, то такой трансформатор будет повышающим.

Все трансформаторы, за счет отсутствия электрической связи между первичной и вторичной обмотками, не имеют электрического контакта вторичной обмотки с питающей сетью.

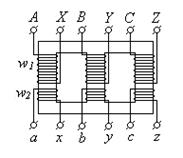Рис. 3.8 – Трехфазный трансформатор

По назначению трансформаторы делятся на: силовые, измерительные, специальные и автотрансформаторы.

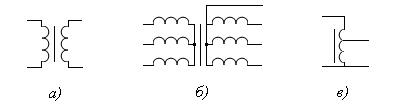
Условные графические изображения трансформаторов показаны на рис. 3.9.

Силовые трансформаторы используются в составе электрических сетей при передаче электроэнергии на расстояние и при ее распределении между потребителями, а также в блоках питания различных промышленных и бытовых устройств. Трансформатор называют силовым, если он служит непосредственно для питания приёмников электрической энергии (нагрузки) или для передачи электрической энергии на большие расстояния. Так, электрическую энергию с полной мощностью S = U I от источника к потребителю можно передать при различных значениях напряжения и тока.

 

Рис.3.9 – Условные графические изображения трансформаторов: а) – однофазного; б) трехфазного; в) автотрансформатора

Чем выше напряжение, тем меньше ток в линии электропередачи (ЛП), тем меньше потери в линии 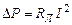. Кроме того, величина тока определяет сечение проводов ЛП, и чем меньше ток, тем меньшее можно выбрать сечение провода, что существенно может снизить вес проводов. Однако при передаче электроэнергии высоким напряжением требуется высокопрочная изоляция и связанные с этим дополнительные затраты на изготовление высоких опор ЛП, использование гирлянд изоляторов и др. Экономически целесообразно передавать большие мощности на большие расстояния высоким напряжением.

Стандартные значения напряжений ЛП (10, 35, 110, 220, 330, 500, 750 кВ) создаются повышающими силовыми трансформаторами. Потребители электроэнергии однофазного и трехфазного тока имеют следующую шкалу номинальных напряжений: 12, 24, 36, 127, 220, 380 В. Для получения этих напряжений используются понижающие силовые трансформаторы.

Измерительные трансформаторы используются для расширения пределов измерения электроизмерительных приборов и для электрического разделения цепи высшего напряжения от цепи низшего напряжения, где находятся приборы и аппараты управления, защиты. Этим самым обеспечивается безопасность обслуживающего персонала. Бывают измерительные трансформаторы тока и трансформаторы напряжения.

Специальные трансформаторы (разделительные, сварочные, вращающиеся и др.) предназначены для выполнения конкретных функций.

Сварочные трансформаторы выполняются понижающими, они могут быть однофазными и трехфазными. Конструктивные особенности таких трансформаторов зависят от вида сварки (дуговая, точечная, шовная и так далее). Они могут иметь повышенный магнитный поток рассеяния.

Разделительные трансформаторы могут иметь первичную и вторичную обмотки с одинаковым числом витков, то есть не преобразуют одно напряжения в другое. Их функция - обеспечить более безопасное питание потребителей от вторичной обмотки, которая электрически изолирована от сети.

В устройствах автоматики трансформаторы могут использоваться для преобразования формы переменного напряжения (импульсные трансформаторы).

Автотрансформаторы, в отличие от обычных трансформаторов, имеют одну обмотку (Рис.3.9, в). В автотрансформаторе питающая сеть электрически связана с сетью потребителя. Для безопасной эксплуатации устройств, питаемых от автотрансформатора, это обстоятельство необходимо всегда учитывать.

 

3.4 Схема замещения однофазного трансформатора

 

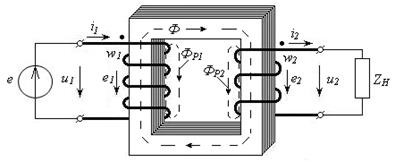
Рассмотрим однофазный трансформатор, схема устройства которого приведена на рис.3.10. К первичной обмотке трансформатора, содержащей w₁ витков, подключен идеальный источник переменной ЭДС е = Е_т sin ωt. Нагрузка Z_H подсоединена к вторичной обмотке, имеющей w₂ витков.

 

Рис.3.10 – Однофазный трансформатор

Здесь следует заметить, что при показанных на рисунке направлениях намотки катушек и направлениях токов i₁ и i₂ магнитные потоки этих катушек будут направлены встречно (убедиться можно, используя правило буравчика). Если бы ток i₂ имел обратное направление по отношению к зажиму второй катушки, помеченному жирной точкой (как в первой катушке), то магнитные потоки катушек сложились бы. Помеченные зажимы называют одноименными.

За счет тока i₁ на входе трансформатора создается падение напряжения u₁ и формируется магнитный поток Ф, общий для первой и второй катушек, и возникает магнитный поток рассеяния Ф_Р1. Так как ЭДС е переменная, то ток i₁ и магнитный поток Ф также будут переменными. За счет изменения магнитного потока Ф в обмотках трансформатора будут создаваться ЭДС (самоиндукции е₁ и взаимной индукции е₂)

 

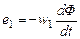и 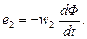(3.20)

 

Положительные направления ЭДС е₁ и тока i₁ в первичной катушке совпадают. Знак «минус» в выражениях (3.20) физически объясняется тем, что в первой катушке ЭДС препятствует изменению тока i₁, а во второй возбуждает ток i₂. За счет тока i₂ во вторичной катушке будет формироваться магнитный поток рассеяния Ф_Р2 и на нагрузке Z_H – напряжение u₂.

Для перехода к схеме замещения необходимо учитывать, что катушки обладают активными сопротивлениями R₁ и R₂ и индуктивными сопротивлениями рассеяния jX_P1 и jX_P2. Потери на гистерезис и индуктивность, связанную с общим для обеих катушек магнитным потоком Ф, можно учесть с помощью идеализированной катушки, обладающей активным сопротивлением R_Г ииндуктивным сопротивлением jωL₀. Представить трансформатор как участок цепи, имеющий два входных и два выходных зажима позволяет Т-образная схема замещения (Рис. 3.11).

Комплексный коэффициент передачи трансформатора по напряжению от входа к выходу

 

(3.21)

 

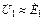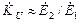Учитывая, что для ненагруженного трансформатора входное напряжение a выходное напряжение , то коэффициент . На основании (3.21) и без учета фаз получим, что коэффициент передачи по напряжению трансформатора

 

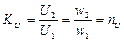(3.22)

Можно также показать, что для токов I₁/I₂≈n_I.

Величину n_U или просто n = U₂/U₁ = w₂ /w₁ называют коэффициентом трансформации по напряжению. Соотношение (3.22) справедливо только для ненагруженного трансформатора.

 

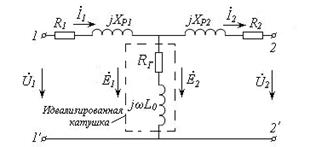
Рис.3.11 – Схема замещения однофазного трансформатора

Если трансформатор имеет несколько вторичных обмоток, то соотношение (3.22) будет применимым для каждой из них. Например, у силового трансформатора, рассчитанного на напряжение сети U₁ =220В число витков первичной обмотки w₁ = 330. Трансформатор содержит две вторичные обмотки с количеством витков w₂= 36 и w₃= 18. Для данного трансформатора первый коэффициент трансформации примерно равен 0,11 и второй 0,055. Выходные напряжения: U_ВЫХ1 = 0,11∙220 ≈ 24В; U_ВЫХ2 = 0,055∙220 ≈ 12В.

Можно также соединив последовательно выходные обмотки получить и третье напряжение U_ВЫХ3 = U_ВЫХ1 + U_ВЫХ2 = 24 + 12 = 36В. Однако здесь необходимо обеспечить согласное включение этих обмоток. При встречном включении получим разность выходных напряжений, что используется редко.

3.5 Режимы работы трансформаторов

 

Важнейшей энергетической характеристикой трансформатора является его номинальная полная мощность, подводимая к первичной обмотке

 

S_HOM = U_1HOM I_1HOM. (3.23)

Различают четыре основные режимы работы трансформатора: номинальный режим; рабочий режим; режим холостого хода; режим короткого замыкания. Рассмотрим эти режимы.

 

Номинальный режим

В этом режиме, когда в первичной обмотке напряжение U₁ = U_1HOM и ток I₁ = I_1HOM обеспечиваются все технические характеристики трансформатора.

 

Рабочий режим

При данном режиме напряжение первичной обмотки близко к его номинальному значению или равно ему (U₁ ≈ U_1HOM), а ток в первичной обмотке меньше или равен номинальному (I₁ ≤ I_1HOM) и зависит от сопротивления нагрузки во вторичной обмотке, то есть I₁ = f(I₂).

 

Режим холостого хода

Это режим, когда трансформатор ненагружен, то есть I₂=0. Он имеет значение при испытании трансформатора, когда проводится опыт холостого хода. При этом должны выполняться условия: U₁ = U_1HOM; I₂ = 0. В ходе опыта по показаниям приборов (вольтметра, ваттметра и амперметра) определяют напряжение U_2Х, ток I_1Х и активную мощность в первичной обмотке Р_1Х. По этим данным для ненагруженного трансформатора находят коэффициент трансформации n = U_2Х / U_{1 HOM} и мощность потерь в магнитопроводе, которая примерно равна Р_1Х.

Ток холостого хода I_1Х будет содержать активную и реактивную составляющие. Активная составляющая определяется в основном потерями в магнитопроводе на гистерезис и на вихревые токи. Потери на активном сопротивлении провода первичной обмотки хотя и будут иметь место, но они незначительны, для трансформаторов с S_HOM ≥ 1000ВА практически не учитываются.

 

Режим короткого замыкания

Если номинальный режим, рабочий режим и режим холостого хода могут иметь место в условиях эксплуатации трансформатора, то в этих условиях режим короткого замыкания является аварийным режимом и его избегают.

При испытании трансформатора опыт короткого замыкания осуществляют при Z_H = 0 и пониженном напряжении U₁ ˂˂ U_1HOM. При этом, изменяя U₁, устанавливают ток в первичной обмотке I_1КЗ ≈ I_1HOM. После этого измеряют напряжение короткого замыкания U_1КЗ и активную мощность потерь в обмотках трансформатора

 

 

Она определяется с помощью ваттметра.

По мощности потерь Р_1КЗ и при I_1КЗ = I_1HOM определяют активное сопротивление короткого замыкания трансформатора

 

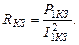(3.24)

 

Активное сопротивление короткого замыкания позволяет определять потери энергии в обмотках и учитывается при расчете температурного режима трансформатора.

Напряжение короткого замыкания U_1КЗ также является важным параметром трансформатора, позволяющим определять изменения вторичного напряжения в рабочем режиме трансформатора. Значение U_1КЗ указывают на щитке трансформатора.

 

Внешняя характеристика трансформатора

Внешняя характеристика трансформатора определяет зависимость вторичного напряжения U₂ от тока нагрузки I₂=I₁/n₂₁ при номинальном входном напряжении U₁ = U_1HOM и постоянном коэффициенте мощности нагрузки φ₂=const.

Аналитическое выражение для внешней характеристики трансформатора имеет вид:

 

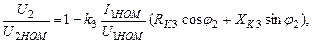(3.25)

 

где k₃ = I₂/I_2НОМ – коэффициент загрузки трансформатора;

I_2НОМ – ток нагрузки при номинальном первичном токе I₁ = I_1HOM; U_2HOM = n₂₁U_1HOM; Х_КЗ – индуктивное сопротивление короткого замыкания.

Из (3.25) следует, что при φ₂=const и возрастании k₃ зависимость U₂ / U_2HOM будет убывать.

 

Коэффициент полезного действия трансформатора

Коэффициентом полезного действия трансформатора (КПД) называется отношение выходной активной мощности Р₂ трансформатора к входной активной мощности Р₁

 

или 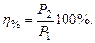(3.26)

 

КПД трансформатора зависит от режима его работы. При номинальном режиме и коэффициенте мощности нагрузки cos φ₂>0,8 для мощных трансформаторов η ≥ 99%. Аналитическое выражение КПД, учитывающее конструктивные особенности и режим работы трансформатора имеет вид:

 

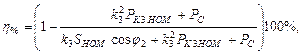(3.27)

 

где Р_{КЗ НОМ} – мощность потерь в проводах обмоток при номинальных токах; Р_С – мощность потерь в магнитопроводе на ги-

стерезис и на вихревые токи; k₃ = I₂/I_2НОМ – коэффициент загрузки трансформатора; cos φ₂ – коэффициент мощности нагрузки.

 

Исследовав функцию η = f(k₃) на экстремум, получим η = η_МАКС при cos φ₂=const и Р_С = Р_{КЗ НОМ}, что будет соответствовать значению k₃ = 1. Однако при проектировании трансформаторов учитывается, что в номинальном режиме трансформаторы работают редко. По этой причине выбирают отношение Р_С / Р_{КЗ НОМ} = 0.25…0.5, что обеспечивает максимум КПД при k₃ = 0.5…0.7.

4 Электрические машины переменного тока

 

Машины переменного тока бывают двух видов. Это синхронные машины и асинхронные. Синхронная машина — это электрическая машина переменного тока, частота вращения ротора которой равна частоте вращения магнитного поля в воздушном зазоре. У асинхронных машин нет такой жесткой зависимости частоты вращения от частоты питающего тока. В общем случае скорость вращения ротора определяется частотой переменного тока и зависит от нагрузки на валу. Оба вида этих машин могут быть однофазными и трехфазными.

Кроме деления на синхронные и асинхронные электрические машины еще делятся по назначению. Это могут быть генераторы – машины, которые преобразует механическую энергию вращения в переменный электрический ток или двигатели, преобразующие электрическую энергию в механическую. Существует еще один класс электрических машин, которые относят к преобразователям электрической энергии. Они преобразуют электрическую энергию тоже в электрическую, но другой частоты или напряжения. Сюда относятся преобразователи частоты (ток 50 Гц в ток 200 или 400Гц) и преобразователи вида тока (переменный в постоянный).

Синхронные машины по большей части применяются в качестве генераторов переменного тока (см. Рис. 2.11) и электродвигателей. Основным достоинством синхронного электродвигателя является то, что в нем легко регулировать скорость вращения вала путем изменения частоты питающего тока. Поэтому их часто применяют в системах автоматики.

Асинхронная машина – это машина, в которой основное магнитное поле статора создаётся переменным электрическим током. Эти машины чаще всего используются в качестве электродвигателей. Они делятся на бесколлекторные и коллекторные.

Большее применение в производстве нашли бесколлекторные асинхронные электродвигатели. Это простые по устройству, надежные и относительно недорогие двигатели.

Коллекторные машины применяются реже, так как они более дороги в производстве и обладают худшими качествами – у них ниже КПД, ниже надежность, большая стоимость и др.).

4.1 Устройство и принцип действия