1. Три деревянных шарика массами m 1, m 2 и m 3 соединены нитями, перекинутыми через блоки так, как показано на рисунке. Шарики массами m 2 и m 3 частично погружены в воду, налитую в цилиндрический сосуд с площадью основания S и система грузов находится в равновесии. На сколько повысится уровень воды в сосуде, если нить, связывающая грузы m 1 и m 2 разрывается, и все шарики оказываются в воде?
Обозначим изменение высоты уровня воды в сосуде – h. Тогда:
, где 
, 
, 
– объемы подводной части шариков при равновесном состоянии системы. 
, 
, 
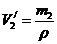, где r – плотность воды. Объемы V 2 и V 3 определим из уравнений, описывающих равновесное состояние шариков.
.
.
2. На главной оптической оси тонкой собирающей положительной линзы на расстоянии 
(F – фокусное расстояние) находится точечный источник (S). Линза разделяется на две равные половины плоскостью, содержащей главную оптическую ось, и одна из этих половин начинает медленно без наклона удаляться от источника по главной оптической оси. Опишите, как выше указанная оптическая система будет отображать источник S.
Задача решается аналитически или путем построений.
1) Всегда существует действительное изображение S 1, находящееся на расстоянии 
от неподвижной части линзы.
2) удаляющаяся часть линзы всегда формирует действительное изображение S 2, которое удаляется от точки S 1, но приближается к заднему фокусу этой части линзы.
3) Как только удаляющаяся часть линзы окажется в интервале [ S 1, S 1 + F ] система формирует третье мнимое изображение источника (точка S 3). При удалении части линзы от точки S 1, т. е. к источнику S и дальше.
4) Когда перемещающаяся часть линзы окажется на расстоянии S 1 + F от первоначального положения, т. е. на расстоянии 
, изображение S 3 раздваивается (мнимое в 
слева и действительное в 
справа).
|
|
5) При небольшом удалении части линзы от точки S 1 + F остается только действительное изображение S 3, которое начинает приближаться к этой части линзы и к источнику S, но S 3 всегда остается правее точки S 2, т. е. отрезок S 2 S 3 всегда уменьшается.
6) С некоторого положения перемещающейся части линзы изображение S 3 приближаясь к ней, начнет удаляться от точки S (но всегда S 2 S 3 уменьшается).
7) На очень большом расстоянии перемещающейся части линзы от первоначального положения точки S 2 и S 3 практически совпадут в заднем фокусе движущейся части линзы.
3. Высокая теплоизолированная трубка заполнена до высоты 25 см льдом, полученным при замерзании воды в этой же трубке. Поверх льда в трубку заливают воду при температуре 10 оС так, что трубка оказывается заполненной до высоты 50 см. После установления теплового равновесия уровень воды в трубке повышается на 0,5 см. Какова была начальная температура льда? Плотность льда 900 кг/м3, удельная теплота плавления льда 340 кДж/кг, удельная теплоемкость льда 2100 Дж/(кг×К), а удельная теплоемкость воды 4200 Дж/(кг×К).
Между льдом и водой происходит теплообмен. При этом часть воды кристаллизуется и устанавливается нулевая температура. Определим массу замерзшей воды.
, где h = 0,25 м, D h = 0,05 м, h 1 высота столбика льда.
.
Составим уравнение теплового баланса
или 
.
Из последнего уравнения находим начальную температуру льда 
.
4. Из шланга лежащего на земле, «бьет» под углом 45о к горизонту струя воды со скоростью v м/с и попадает на наклонную поверхность с углом наклона 45о и отстоящую по горизонтали от шланга на расстоянии l м. Площадь сечения отверстия шланга S см2. Определить массу струи воды, находящейся в воздухе.
|
|
Масса воды определяется по формуле 
, где t – время движения воды до соприкосновения с поверхностью.
Для траектории воды: 
(1), 
. Выражая из уравнения координаты по оси x время, и подставляя во второе уравнение 
, получим уравнение траектории струи:
.
Уравнение прямой, принадлежащей плоскости 
. Учитывая, что 
, получаем 
и 
(2). Сделаем замену (1) в (2): 
. Следовательно, масса струи воды, находящейся в воздухе равна 
.
Примечание: на олимпиаде были предложены значения v = 6 м/с, S = 3 см2, l = 5 м, a = 45о. Подставляя эти значения в формулу 
кг. Но дальность полета струи 
м, струя не долетает до наклонной поверхности. Следовательно,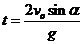 
и 
кг.
5. Какой электрический ток пойдет по подводящим проводам цепи, присоединенной к источнику с очень большой выходной мощностью, при коротком замыкании, если на спиралях сопротивлением 400 Ом и 100 Ом при поочередном их подключении в цепь, выделяется одинаковая мощность 400 Вт?
Значения силы тока при подключении спиралей и коротком замыкании равно:
, 
, 
.
Напряжение на спиралях определим по формуле:
, 
, 
, 
, где R o – сопротивление подводящих проводов. 
, 
, 
.
, 
.
Разделив, левые и правые части уравнений, находим
.