теплопроводность
1.1. Основной закон теплопроводности
Если в твердом теле, неподвижной жидкости или газе температура в различных точках неодинакова, то, как показывает опыт, теплота самопроизвольно переносится от участков с более высокой температурой к участкам с более низкой температурой. Такой процесс называется теплопроводностью. Перенос внутренней энергии в форме теплоты при этом осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Поэтому при его изучении необходимо установить понятия температурного поля и градиента температуры
а) Температурное поле. Под температурным полем понимают совокупность значений температуры во всех точках тела в данный момент времени.
В общем случае математическое описание температурного поля имеет вид:
t = f (x, y, z, t). (1.1)
Это уравнение трехмерного неустановившегося (нестационарного) температурного поля, так как температура зависит от положения точки тела (ее координат) и времени t. Если температура в любой точке тела не изменяется во времени, а является лишь функцией координат, то имеет место трехмерное установившееся (стационарное) температурное поле:
t = φ (x, y, z). (1.1а)
В случае одномерного стационарного температурного поля температура изменяется только вдоль одной координаты t = f (x).
б) Градиент температуры. При любом температурном поле имеются точки с одинаковой температурой. Геометрическое место таких точек образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности друг с другом не пересекаются; они замыкаются на себя или оканчиваются на границах тела. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности (например, направление х, рис. 1.1). При этом наибольший перепад температуры на участке единичной длины происходит в направлении нормали (n) к изотермической поверхности.
Рис. 1.1. К определению температурного градиента
Градиент температуры (gradt) – есть вектор, направленный по нормали n к изотермической поверхности в сторону возрастания температуры, модуль которого численно равен производной от температуры по этому направлению
(1.2)
где 
- единичный вектор нормали. Проекции вектора gradt на координатные оси:
(1.2а)
Градиент температуры характеризует неравномерность ее распределения в объеме системы и представляет собой максимальную скорость изменения температуры вдоль нормали к изотермической поверхности.
в) Тепловой поток. В теории теплообмена используются понятия теплового потока Q, Вт и поверхностной плотности теплового потока q, Вт/м2.
Полным тепловым потоком Q называется количество теплоты, проходящее через какую-либо изотермическую поверхность F в единицу времени.
Поверхностной плотностью теплового потока q называется количество теплоты, проходящее в единицу времени через единицу заданной изотермической поверхности тела.
Тепловой поток и поверхностная плотность теплового потока – векторы, направленные по нормали к изотермической поверхности в сторону убывания температуры (противоположно направлению температурного градиента, рис. 1.1).
г) Закон Фурье. Основной закон теплопроводности сформулирован Фурье на основании обобщения опытных данных. Согласно закону Фурье вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален градиенту температуры:
(1.3)
Знак минус обусловлен вторым законом термодинамики, согласно которому теплота переносится в направлении снижения температуры.
Уравнение (1.3) является математическим выражением закона Фурье, который лежит в основе всех теоретических и экспериментальных исследований процессов теплопроводности.
д) Коэффициент теплопроводности. Опытным путем установлено, что коэффициент пропорциональности в уравнении (1.3) есть физический параметр вещества. Он характеризует способность вещества проводить теплоту и называется коэффициентом теплопроводности. Коэффициент теплопроводности l, Вт/(м×К) численно равен плотности теплового потока при градиенте температуры равном единице. Он зависит от природы вещества, температуры, давления. Для тепловых расчетов часто применяют средние табличные значения коэффициента теплопроводности, взятые по данным теплотехнических справочников [5,8].
1.2. Дифференциальное уравнение теплопроводности
Уравнение выводится на основе закона сохранения энергии и закона Фурье. При выводе считаем тело однородным и изотропным, физические параметры постоянными, внутренние источники теплоты в теле qV, Вт/м3 распределенными равномерно. Закон сохранения энергии в данном случае может быть сформулирован следующим образом: количество теплоты dQ1, введенное в элементарный объем dV извне за время dt вследствие теплопроводности, и dQ2 – от внутренних источников теплоты равно изменению внутренней энергии вещества dQ, содержащейся в элементарном объеме:
(1.4)
Количество теплоты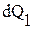 
,определяемое на основании закона Фурье, равно:
;
.
Изменение внутренней энергии вещества dQ
.
Подставляя значения 
, 
, 
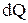в (1.4) получаем:
или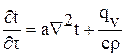 
, (1.5)
где l, с, r - коэффициент теплопроводности, Вт/(м×К), теплоемкость, Дж/(кг×К) и плотность, кг/м3 вещества;
- коэффициент температуропроводности тела, характеризующий скорость изменения его температуры;
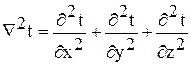- оператор Лапласа.
Выражение (1.5) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменением температуры в любой точке тела, в которой происходит процесс теплопроводности.
Коэффициент пропорциональности а, м2/с в уравнении (1.5) является физическим параметром вещества и называется коэффициентом температуропроводности. Он важен для нестационарных тепловых процессов. Если коэффициент теплопроводности l характеризует способность тела проводить теплоту, то коэффициент температуропроводности а – быстроту выравнивания температуры тела во времени, т.е. является мерой теплоинерционных свойств тела. Выравнивание температуры во всех точках тела (
пропорционально а) будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности.
Если система тел не содержит внутренних источников теплоты (qV = 0), тогда выражение (1.5) принимает форму уравнения Фурье
; (1.6)
для стационарного состояния в этом случае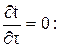 
.
Условия однозначности. Дифференциальное уравнение (1.5) выведено на основе общих законов физики и описывает явления теплопроводности в самом общем виде. Для решения конкретных задач необходимо к уравнению присоединить математическое описание частных особенностей рассматриваемого процесса (условия однозначности). Условиями однозначности называется совокупность условий, включающих геометрические условия (форма и размеры тела), его теплофизические свойства, задаваемые параметрами a, l, с, r и др., начальные условия – распределение температуры внутри тела в начальный момент времени; условия теплообмена на границах тела с внешней средой (граничные условия).
Граничные условия на внешних поверхностях тела для любого момента времени t можно задавать следующими способами:
- распределением температуры на поверхности тела 
= f (x, y, z, t) или = const;условия первого (I) рода;
- плотностью теплового потока для любой точки поверхности 
= f (x, y, z, t) или = const; условия второго (II) рода;
- температурой окружающей среды 
и законом теплообмена между поверхностью тела и окружающей средой; граничные условия третьего (III) рода.
В качестве простейшего соотношения, связывающего плотность теплового потока qна границе тела с температурой поверхности , принимается закон Ньютона
(1.8)
где α– коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой и численно равный плотности теплового потока q при разности температур поверхности тела и окружающей среды в один градус, Вт/(м2×К).
Определив плотность теплового потока q из выражения (1.3) и из соотношения (1.8), получим аналитическое выражение граничных условий III рода
или 
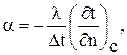(1.9)
где 
- температурный напор стенка – окружающая среда.
Индекс «с» означает, что температурный градиент относится к поверхности тела.
Существуют еще граничные условия IV рода, когда рассматриваемое тело находится в плотном контакте с другим телом. Аналитическое выражение граничных условий IV рода описывает равенство тепловых потоков при одинаковых температурах соприкасающихся точек.
Дифференциальное уравнение теплопроводности и аналитическое выражение условий однозначности дают полную математическую формулировку конкретной задачи теплопроводности. Наиболее простые соотношения получаются при установлении стационарного режима, в котором температура тела не изменяется во времени
1.3. Теплопроводность при стационарном режиме
и граничных условиях первого рода
Рассмотрим теплопроводность тел простейшей геометрической формы, на боковых поверхностях которых поддерживается постоянная температура 
и 
. При этих условиях температура изменяется только по сечению тела, температурное поле одномерно.
При выводе расчетных зависимостей будем считать, что стенки однородны по физическим свойствам и изотропны, тепловыделение в них отсутствует. Коэффициент теплопроводности λ принимаем постоянным λ = const, не зависящим от температуры и других факторов, режим стационарным (установившемся).
Решение задачи включает: определение закона распределения температуры по сечению стенки и вычисление теплового потока, проходящего через стенку.
Плоская стенка (рис. 1.2). Дифференциальное уравнение теплопроводности и условия однозначности для плоской стенки имеют вид:
; (1.10)
; 
,
где δ – толщина стенки.
Рис. 1.2. Распределение температуры в плоской стенке
при граничных условиях первого (I) рода
Интегрируя (1.10) получаем
и 
, (1.12)
где 
и 
- постоянные интегрирования, значения которых находятся из граничных условий (1.11).
При х = 0 из (1.11) и (1.12) находим, что 
, а при х = δ 
, 
. Подставляя и в (1.12) получим уравнение температурного поля плоской стенки
. (1.13)
Из выражения (1.13) следует, что температура в стенке изменяется по линейному закону при условии λ = const.
Согласно закону теплопроводности Фурье плотность теплового потока через стенку
. (1.14)
Плотность теплового потока прямопропорциональна коэффициенту теплопроводности, разности температур на поверхностях стенки и обратно пропорционально толщине стенки d.
Запишем соотношение (1.14) в форме закона Ома
. (1.15)
Величину 
К/(Вт/м2) называют по аналогии с электрическими явлениями термическим сопротивлением плоской стенки. Оно характеризует падение температуры в стенке при переносе единицы плотности теплового потока.
Общее количество теплоты Q, Дж, передаваемое через поверхность стенки площадью F за время t,
. (1.16)
Легко доказать, что в общем случае для плоской стенки, состоящей из n слоев однородных по физическим свойствам и плотно прилегающих друг к другу, выполненных из различных материалов разной толщины плотность теплового потока q
, (1.17)
где 
- полное термическое сопротивление многослойной плоской стенки, равное сумме термических сопротивлений n слоев, 
, 
- температуры на внешних поверхностях многослойной стенки.
Цилиндрическая стенка (рис. 1.3). Считаем, что полый цилиндр (труба) является прямым, круглым, бесконечно длинным. Температуры на внутренней и внешней поверхностях цилиндрической стенки и поддерживаются постоянными, причем > . Температура изменяется только вдоль радиуса t = f(r), изотермические поверхности являются концентрическими цилиндрическими поверхностями. Дифференциальное уравнение теплопроводности в этом случае принимает вид:
. (1.18)
Рис. 1.3. Распределение температуры в цилиндрической стенке
при граничных условиях первого (I) рода
Введем новую переменную u, которая является градиентом температуры (gradt)
.
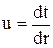Подставляя u в уравнение (1.18) получим дифференциальное уравнение первого порядка с разделяющимися переменными
. (1.19)
Интегрируя, получаем ur = .
Подставив 
, разделив переменные 
, интегрируя имеем
, (1.20)
где , - постоянные интегрирования.
Распределение температуры по сечению цилиндрической стенки описывается уравнением логарифмической кривой.
Из граничных условий первого рода находим постоянные и и, воспользовавшись законом Фурье, вычисляем тепловой поток Q, Вт, проходящий через участок цилиндрической поверхности длиною l.
(1.21)
где 
, 
- внутренний и наружный диаметры стенки.
Тепловой поток может быть отнесен к площади внутренней или внешней поверхности трубы, либо к ее длине.
Тепловой поток отнесенный к единице длины 
, Вт/м, называется линейной плотностью теплового потока.
; 
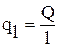. (1.22)
Величина 
называется линейным термическим сопротивлением цилиндрической стенки, (К/Вт×м).
В практических расчетах при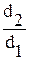 
≤ 2 (цилиндрическая стенка является тонкостенной) линейный тепловой поток с погрешностью менее 5% можно рассчитывать по формуле плоской стенки
, (1.23)
где d - средний диаметр стенки, d = 0,5 ( + ),
d - толщина стенки, d = 0,5 ( - ).
Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для случая многослойной плоской стенки, просуммировать термические сопротивления отдельных слоев.
, (1.24)
где 
- полное линейное термическое сопротивление многослойной цилиндрической стенки.
Расчет температур на границах плотно соприкасающихся слоев в обеих случаях (плоская и цилиндрическая стенки) проводится по формуле:
(1.25)
где 
- температура за любым слоем (i = к);
- для плоской стенки, 
- для цилиндрической стенки.
1.4. Теплопроводность плоской и цилиндрической стенок при