(ТЕПЛОПЕРЕДАЧА)
В энергетических установках часто встречается теплообмен между двумя средами (теплоносителями) через разделяющую их твердую стенку, который называют теплопередачей. В этом случае теплота от более нагретого теплоносителя теплоотдачей и тепловым излучением передается к стенке, внутри стенки теплообмен происходит за счет теплопроводности, а от противоположной поверхности стенки осуществляется теплоотдачей к менее нагретому теплоносителю.
В теории теплопроводности процесс теплопередачи понимается как теплопроводность стенки при граничных условиях третьего рода. Рассмотрим задачу о теплопроводности стенки, разделяющей две среды с температурами  и
и  (
( >
>  ) и коэффициентами теплоотдачи
) и коэффициентами теплоотдачи  и
и  , характеризующими интенсивность теплообмена на наружных поверхностях стенки. Считаем, что температура стенки зависит только от координаты, являющейся нормалью к изотермическим поверхностям (одномерная задача).
, характеризующими интенсивность теплообмена на наружных поверхностях стенки. Считаем, что температура стенки зависит только от координаты, являющейся нормалью к изотермическим поверхностям (одномерная задача).
Плоская стенка (рис. 1.4). Плоская стенка толщиной d, коэффициент теплопроводности l разделяет две жидкости с различной температурой  и
и  . В гидравлике понятие жидкость включает как жидкие, так и газообразные среды. Коэффициенты теплоотдачи со стороны горячей и холодной жидкостей
. В гидравлике понятие жидкость включает как жидкие, так и газообразные среды. Коэффициенты теплоотдачи со стороны горячей и холодной жидкостей  и
и  . Считаем, что величины l,
. Считаем, что величины l,  ,
,  ,
,  ,
,  постоянны, а температурное поле в стенке - одномерное.
постоянны, а температурное поле в стенке - одномерное.
Рассматриваемый процесс переноса теплоты от одной жидкости (горячий теплоноситель) к другой (холодный теплоноситель) через разделяющую их твердую стенку, как уже отмечалось, называется теплопередачей.
В стационарном режиме количество теплоты, которое передается от горячей жидкости поверхности стенки, проходит через нее и отдается холодной жидкости, одно и то же.
Плотность теплового потока, отдаваемого жидкостью с температурой  поверхности стенки с температурой
поверхности стенки с температурой  в соответствии с уравнением теплоотдачи (1.8)
в соответствии с уравнением теплоотдачи (1.8)
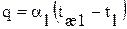 , (1.26)
, (1.26)
та же плотность передается через стенку за счет теплопроводности
 , (1.27)
, (1.27)
от поверхности стенки с температурой 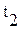 холодной жидкости путем теплоотдачи
холодной жидкости путем теплоотдачи
 . (1.28)
. (1.28)
Решая уравнения (1.26), (1.27), (1.28) относительно разности температур и складывая их почленно получаем:
 . (1.29)
. (1.29)
Величина
 (1.30)
(1.30)
называется коэффициентом теплопередачи, Вт/(м2×К). Коэффициент теплопередачи k характеризует интенсивность процесса теплопередачи и числено равен количеству теплоты, которое передается через поверхность стенки площадью 1 м2 за одну секунду при разности температур жидкостей 1 К.
С учетом (1.30) уравнение (1.29) имеет вид
 . (1.31)
. (1.31)
Полный тепловой поток Q, Вт равен:
 . (1.32)
. (1.32)

Рис. 1.4. Теплопередача через плоскую стенку
Соотношение (1.31) или (1.32) называется уравнением теплопередачи.
Величина 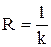 , К/(Вт∙м2), обратная коэффициенту теплопередачи,
, К/(Вт∙м2), обратная коэффициенту теплопередачи,
 (1.33)
(1.33)
называется полным термическим сопротивлением теплопередачи и является суммой частных термических сопротивлений: стенки  , теплоотдачи со стороны горячей
, теплоотдачи со стороны горячей  и холодной
и холодной  жидкостей:
жидкостей:
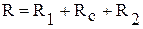 .
.
Для случая многослойной плоской стенки, омываемой жидкостями, берется сумма термических сопротивлений слоев стенки:
 (1.34)
(1.34)
Цилиндрическая стенка (рис. 1.5). Линейная плотность теплового потока  , Вт/м, проходящего через цилиндрическую стенку, находится по формулам:
, Вт/м, проходящего через цилиндрическую стенку, находится по формулам:
- теплоотдача на внутренней поверхности
 , (1.35)
, (1.35)
- распространение теплоты в стенке теплопроводностью
 , (1.36)
, (1.36)

Рис. 1.5. Теплопередача через цилиндрическую стенку
- теплоотдача на внешней поверхности стенки
 . (1.37)
. (1.37)
Из соотношений (1.35), (1.36), (1.37) находим разности температур и складывая их почленно, определяем  - линейную плотность теплового потока.
- линейную плотность теплового потока.
 , (1.38)
, (1.38)
где выражение
 (1.39)
(1.39)
называют линейным коэффициентом теплопередачи, Вт/(м×К).
Уравнение теплопередачи через цилиндрическую стенку имеет вид:
 . (1.40)
. (1.40)
Линейный коэффициент теплопередачи  числено равен количеству теплоты, проходящей в 1 с через цилиндрическую поверхность длиной 1 м при разности температур между жидкостями 1 К.
числено равен количеству теплоты, проходящей в 1 с через цилиндрическую поверхность длиной 1 м при разности температур между жидкостями 1 К.
Величина, обратная линейному коэффициенту теплопередачи,
 (1.41)
(1.41)
называется линейным термическим сопротивлением теплопередачи через цилиндрическую стенку, К/(Вт/м).
Величины  и
и  - называются частными сопротивлениями теплоотдачи на соответствующих поверхностях или поверхностными сопротивлениями, а величина
- называются частными сопротивлениями теплоотдачи на соответствующих поверхностях или поверхностными сопротивлениями, а величина  - линейным термическим сопротивлением теплопроводности цилиндрической стенки:
- линейным термическим сопротивлением теплопроводности цилиндрической стенки:
 . (1.42)
. (1.42)
Аналогично плоской стенки (1.34), для случая многослойной цилиндрической стенки, омываемой жидкостями, берется сумма линейных термических сопротивлений слоев.
1.5. Регулирование интенсивности теплопередачи
В практике создания и эксплуатации энергетических установок, трубопроводов и другого оборудования приходится решать задачи увеличения или снижения тепловых потоков, идущих через поверхности различной формы от одной среды к другой. При этом одновременно решаются и другие задачи, например, обеспечение безопасности и надежности, простоты конструкции и ее технологичности, оптимальной стоимости, защиты окружающей среды и др. [11].
Интенсификация теплопередачи. Так как теплопередача представляет собой сложное явление, то ее интенсификация связана с анализом частных сопротивлений, характеризующих этот процесс. Существуют следующие основные направления интенсификации теплопередачи в энергетических установках и аппаратах.
1. Создание развитых поверхностей теплообмена за счет их оребрения со стороны окружающей среды с малым коэффициентом теплоотдачи. При этом часто одновременно решается задача минимизации массы ребристой стенки при заданной степени интенсификации.
2. Изменение гидродинамических условий на поверхности теплообмена за счет искусственной турбулизации: создание различных видов шероховатостей на обтекаемых поверхностях, использование всевозможных турбулизирующих вставок, применение различных физических эффектов (пульсирующее поле давлений, электромагнитное поле) и др. С другой стороны, турбулизация потока увеличивает его гидравлическое сопротивление, что требует дополнительных затрат на создание потока жидкости через систему [5].
3. Оптимизация геометрических размеров поверхностей теплообмена. Оптимальное уменьшение диаметра труб в теплообменнике позволяет увеличивать их число, а, следовательно, и общую поверхность теплообмена при сокращении его габаритов.
Рассмотрим некоторые возможные пути интенсификации теплопередачи на примере плоской стенки. Из уравнения (1.29) следует, что при заданных температурах плотность теплового потока через плоскую стенку зависит от коэффициента теплопередачи, увеличение которого может быть достигнуто за счет применения более тонкой стенки, выбора материала с высокой теплопроводностью или увеличения коэффициентов теплоотдачи. Если термическое сопротивление стенки мало  , то в соответствии с (1.30) коэффициент теплопередачи
, то в соответствии с (1.30) коэффициент теплопередачи
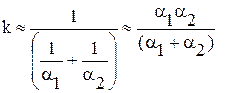 (1.43)
(1.43)
и всегда меньше самого малого коэффициента теплоотдачи. Для увеличения kнеобходимо увеличивать наименьшее из значений коэффициентов теплоотдачи  или
или  . Если,
. Если,  =
=  , увеличение коэффициента теплопередачи возможно за счет роста любого из α. При больших значениях коэффициентов теплоотдачи
, увеличение коэффициента теплопередачи возможно за счет роста любого из α. При больших значениях коэффициентов теплоотдачи  и
и  коэффициент теплопередачи
коэффициент теплопередачи  в значительной степени зависит от теплопроводности и толщины стенки.
в значительной степени зависит от теплопроводности и толщины стенки.
При передаче теплоты через цилиндрическую стенку из (1.39) следует, что термические сопротивления  и
и  зависят не только от коэффициентов теплоотдачи, но и от размеров поверхностей. Если
зависят не только от коэффициентов теплоотдачи, но и от размеров поверхностей. Если  и
и  малы, то термическое сопротивление теплоотдачи можно уменьшить путем увеличения соответствующей поверхности.
малы, то термическое сопротивление теплоотдачи можно уменьшить путем увеличения соответствующей поверхности.
Для уменьшения термического сопротивления теплопередачи через стенку используется оребрение ее внешних поверхностей теплообмена. Ребристые поверхности изготавливаются в виде сплошных отливок либо отдельных ребер, приваренных к поверхностям.
Отношение площади оребренной поверхности  к площади гладкой поверхности
к площади гладкой поверхности 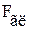 называют коэффициентом оребрения
называют коэффициентом оребрения 
Коэффициент теплопередачи (1.30) для плоской стенки с оребрением с одной стороны в этом случае имеет вид:
 . (1.44)
. (1.44)
Соотношение (1.44) получено в предположении, что температура основной поверхности и оребренной одинакова. В действительности в элементах оребрения наблюдается градиент температуры и степень тепловой эффективности оребренной поверхности по высоте ребра неодинаковы. Она оценивается коэффициентом эффективности этой поверхности, определяемым из выражения
 ,
,
где  - площадь поверхности оребрения;
- площадь поверхности оребрения;
F - полная площадь поверхности теплообмена со стороны оребрения;
 - коэффициент эффективности ребра - отношение средней разности температур оребренной поверхности и окружающей среды к разности температур поверхности, несущей оребрение, и окружающей среды. Тогда соотношение (1.44) имеет вид:
- коэффициент эффективности ребра - отношение средней разности температур оребренной поверхности и окружающей среды к разности температур поверхности, несущей оребрение, и окружающей среды. Тогда соотношение (1.44) имеет вид:
 .
.
Так как температура по высоте ребра переменна, изменяется и коэффициент теплоотдачи  , значение которого может быть определено только опытным путем [2].
, значение которого может быть определено только опытным путем [2].
Температурное поле ребра может быть найдено расчетным путем [1].
При использовании метода оребрения для интенсификации теплопередачи следует иметь в виду, что если коэффициент теплоотдачи  , на внутренней поверхности значительно меньше коэффициента теплоотдачи
, на внутренней поверхности значительно меньше коэффициента теплоотдачи 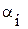 на наружной поверхности (
на наружной поверхности ( «
«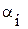 ),увеличение наружной поверхности целесообразно до тех пор, пока не наступит равенство
),увеличение наружной поверхности целесообразно до тех пор, пока не наступит равенство  =
=  . Дальнейшее увеличение наружной поверхности
. Дальнейшее увеличение наружной поверхности  малоэффективно.
малоэффективно.
Тепловая изоляция (снижение теплопередачи). Для уменьшения теплового потока (тепловых потерь) в общем случае необходимо увеличивать термическое сопротивление теплопередачи. Это обеспечивается тепловой изоляцией, выполненной из теплоизоляционных материалов с низким значением коэффициента теплопроводности. Однако не всегда увеличение толщины слоя изоляции приводит к увеличению термического сопротивления теплопередачи. Знание механизма теплопередачи в таких случаях выгодно экономически, поскольку позволяет избежать многих ошибок при выполнении теплоизоляционных работ.
Рассмотрим влияние изменения наружного диаметра изоляции  на термическое сопротивление теплоизолированной стенки (рис. 1.6). В соответствии с (1.41) термическое сопротивление теплопередачи изолированной цилиндрической стенки определяется выражением:
на термическое сопротивление теплоизолированной стенки (рис. 1.6). В соответствии с (1.41) термическое сопротивление теплопередачи изолированной цилиндрической стенки определяется выражением:
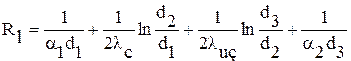 , (1.45)
, (1.45)
или
 ,
,
где  и
и  - внутренний и наружный диаметры стенки;
- внутренний и наружный диаметры стенки;
 и
и  - коэффициенты теплопроводности материала стенки и изоляции.
- коэффициенты теплопроводности материала стенки и изоляции.
При постоянных значениях  величина
величина  будет зависеть только от внешнего диаметра изоляции
будет зависеть только от внешнего диаметра изоляции  , так как термические сопротивления теплоотдачи
, так как термические сопротивления теплоотдачи  и теплопроводности
и теплопроводности  постоянны. С ростом
постоянны. С ростом  увеличивается термическое сопротивление теплопроводности изоляции
увеличивается термическое сопротивление теплопроводности изоляции  , а термическое сопротивление теплоотдачи
, а термическое сопротивление теплоотдачи  уменьшается. Очевидно, что полное сопротивление
уменьшается. Очевидно, что полное сопротивление  будет определяться характером изменения его составляющих
будет определяться характером изменения его составляющих  и
и  (рис. 1.6.).
(рис. 1.6.).
Для того, чтобы выяснить, как будет меняться  при изменении наружного диаметра изоляции
при изменении наружного диаметра изоляции  , возьмем первую производную функции
, возьмем первую производную функции  и приравняем ее нулю:
и приравняем ее нулю:
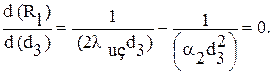
Значение  , найденное из этого выражения, соответствует экстремальной точке кривой, изображающей на рис. 1.6 функцию
, найденное из этого выражения, соответствует экстремальной точке кривой, изображающей на рис. 1.6 функцию  . Вторая производная функции
. Вторая производная функции  в этой точке будет больше нуля. Следовательно, найденному значению
в этой точке будет больше нуля. Следовательно, найденному значению  соответствуют минимальное термическое сопротивление теплопередачи и максимальная плотность теплового потока. В этом случае наружный диаметр
соответствуют минимальное термическое сопротивление теплопередачи и максимальная плотность теплового потока. В этом случае наружный диаметр  называется критическим диаметром изоляции и обозначается
называется критическим диаметром изоляции и обозначается
 . (1.46)
. (1.46)

Рис. 1.6. Зависимость термического сопротивления
изолированной цилиндрической стенки от наружного диаметра
В интервале от  до
до  с увеличением наружного диаметра
с увеличением наружного диаметра  термическое сопротивление теплоотдачи наружной поверхности
термическое сопротивление теплоотдачи наружной поверхности  оказывает большое влияние на общее термическое сопротивление теплопередачи изолированной стенки, чем термическое сопротивление теплопроводности изоляции
оказывает большое влияние на общее термическое сопротивление теплопередачи изолированной стенки, чем термическое сопротивление теплопроводности изоляции  , и поэтому
, и поэтому  уменьшается. При
уменьшается. При  >
>  с увеличением наружного диаметра
с увеличением наружного диаметра  термическое сопротивление теплопроводности изоляции
термическое сопротивление теплопроводности изоляции  оказывает доминирующее влияние на
оказывает доминирующее влияние на  , которое в этом случае растет (рис. 1.6.).
, которое в этом случае растет (рис. 1.6.).
На рис. 1.7. показано изменение тепловых потерь  в зависимости от диаметра трубы покрытой слоем изоляции. Если для данного теплоизоляционного материала величина
в зависимости от диаметра трубы покрытой слоем изоляции. Если для данного теплоизоляционного материала величина  больше диаметра трубы
больше диаметра трубы  , (
, ( >
>  ), то линейный тепловой поток
), то линейный тепловой поток  сначала возрастает (линия 1), достигает максимума при
сначала возрастает (линия 1), достигает максимума при  , затем начинает снижаться и только при
, затем начинает снижаться и только при  >
>  оказывается меньше, чем он был, когда изоляция отсутствовала. Таким образом, выбранная изоляция обеспечивает снижение тепловых потерь, только начиная с диаметра
оказывается меньше, чем он был, когда изоляция отсутствовала. Таким образом, выбранная изоляция обеспечивает снижение тепловых потерь, только начиная с диаметра  , при котором тепловые потери изолированных и неизолированных труб одинаковы. Следовательно, некоторый слой тепловой изоляции
, при котором тепловые потери изолированных и неизолированных труб одинаковы. Следовательно, некоторый слой тепловой изоляции  не будет оправдывать своего назначения. Кривая 2 соответствует случаю, когда
не будет оправдывать своего назначения. Кривая 2 соответствует случаю, когда  <
<  .
.
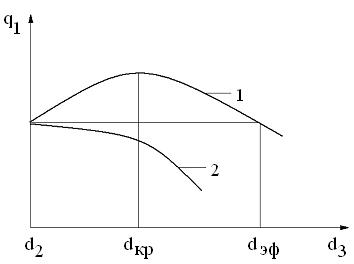
Рис. 1.7. Критический диаметр изоляции
1 –  >
>  ; 2 –
; 2 –  <
< 
Таким образом, если стоит задача уменьшения теплового потока, то в качестве изоляционного надо выбрать материал с таким значением  , для которого величина
, для которого величина  будет ниже внешнего диаметра оголенного трубопровода либо равна ему. С учетом этого, используя выражение (1.46) получим условие эффективной работы тепловой изоляции
будет ниже внешнего диаметра оголенного трубопровода либо равна ему. С учетом этого, используя выражение (1.46) получим условие эффективной работы тепловой изоляции
 или
или 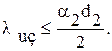 (1.47)
(1.47)
Если по каким-то соображениям (например, при изоляции электрических проводов) требуется нанести слой материала, не ухудшая условия теплообмена охлаждения, то необходимо взять материал, для которого  >
>  .
.
1.6. Теплопроводность при наличии внутренних источников теплоты
Рассмотрим стационарную теплопроводность  симметричных тел (пластины, цилиндра), внутри которых действуют равномерно распределенные источники теплоты мощностью
симметричных тел (пластины, цилиндра), внутри которых действуют равномерно распределенные источники теплоты мощностью  , Вт/м3 (
, Вт/м3 ( = const), а с поверхности происходит теплообмен с окружающей средой постоянной температуры
= const), а с поверхности происходит теплообмен с окружающей средой постоянной температуры  (граничные условия третьего рода).
(граничные условия третьего рода).
Неограниченная пластина (рис. 1.8.). Для рассматриваемой задачи дифференциальное уравнение теплопроводности и аналитическое выражение условий однозначности имеют следующий вид:
 (1.48)
(1.48)
 (1.49)
(1.49)
После интегрирования (1.48) получаем:
 (1.50)
(1.50)
 (1.51)
(1.51)
Константы интегрирования находятся из граничных условий (1.49). При х = 0 из (1.50) определяем  = 0. При х = d из (1.49) и (1.50) получаем
= 0. При х = d из (1.49) и (1.50) получаем
 .
.
Из последнего выражения находим температуру поверхности пластины:
 . (1.52)
. (1.52)
Подставляя значение  в уравнение (1.51) определяем
в уравнение (1.51) определяем 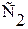
 .
.
Подставляя значение констант  и
и 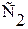 в (1.51) находим уравнение температурного поля пластины:
в (1.51) находим уравнение температурного поля пластины:
 , (1.53)
, (1.53)
где t(x)- температура пластины на расстоянии х от средней плоскости.
В рассматриваемой задаче тепловой поток изменяется вдоль оси х 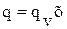 . При х = 0, q = 0 (это следует из условия, что при х = 0 имеем
. При х = 0, q = 0 (это следует из условия, что при х = 0 имеем  ). Тепловой поток с единицы поверхности пластины при х = δ
). Тепловой поток с единицы поверхности пластины при х = δ

и общее количество теплоты, отданное всей поверхностью пластины в единицу времени,
 (1.54)
(1.54)
где F - боковая поверхность пластины.
Из уравнения (1.53) следует, что распределение температуры в плоской стенке в случае симметричной задачи подчиняется распределению по параболическому закону.
Если в уравнении (1.53) положить α → ∞, то полученное выражение будет представлять температурное поле для граничных условий первого рода, ибо при α → ∞ получим 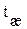 >
>  .
.
Цилиндрический стержень. Решая дифференциальное уравнение теплопроводности для неограниченного цилиндрического стержня


Рис. 1.8. Распределение температуры в пластине
при внутреннем тепловыделении
и используя условия однозначности

получают уравнение температурного поля цилиндрического стержня:
 , (1.55)
, (1.55)
где  - радиус стержня;
- радиус стержня;
 - температура стержня на расстоянии r от оси.
- температура стержня на расстоянии r от оси.
Уравнение (1.55) показывает, что распределение температуры в круглом стержне подчиняется параболическому закону.
Из уравнения (1.55) при r = 0 найдем температуру на оси цилиндра:
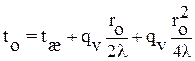 . (1.56)
. (1.56)
Плотность теплового потока на поверхности цилиндра:
 . (1.57)
. (1.57)
Полный тепловой поток с поверхности цилиндра:
 .
.
Из уравнения (1.57) следует, что плотность теплового потока зависит от мощности внутренних источников  и от величины внешней поверхности, через которую проходит тепловой поток.
и от величины внешней поверхности, через которую проходит тепловой поток.
1.7. Нестационарная теплопроводность
Процессы передачи теплоты теплопроводностью, когда температурное поле в теле изменяется не только в пространстве, но и во времени, называются нестационарными. В нестационарных процессах, встречающихся в энергетических установках, тело стремится к тепловому равновесию или температура тела претерпевает периодические изменения. К первой группе относятся процессы нагрева или охлаждения тел, помещенных в среду с заданным тепловым состоянием (например, нагрев болванки в печи, охлаждение элементов энергетической установки после ее останова и др.). Ко второй группе - процессы, происходящие в периодически действующих подогревателях (например, нагрев воздуха в регенераторе, насадка которого то нагревается горячими газами, то охлаждается нагреваемым воздухом и др.).
Из-за тепловой инерции тело, имеющее в начальный момент времени постоянную по объему температуру  и помещенное в среду с более высокой постоянной температурой
и помещенное в среду с более высокой постоянной температурой  >
>  , прогревается неравномерно по объему. С течением времени изменение температуры в центре
, прогревается неравномерно по объему. С течением времени изменение температуры в центре  отстает от ее изменения на поверхности
отстает от ее изменения на поверхности  . По мере прогревания температура в каждой точке тела стремится к некоторому предельному значению, близкому к температуре окружающей среды
. По мере прогревания температура в каждой точке тела стремится к некоторому предельному значению, близкому к температуре окружающей среды  .
.
Аналитическое описание процесса нестационарной теплопроводности включает в себя дифференциальное уравнение (1.5) и условия однозначности.
Решение задачи нестационарной теплопроводности заключается в отыскании функции  или
или  , которая удовлетворяла бы дифференциальному уравнению и условиям однозначности, а также определению зависимости количества теплоты от времени для любой точки тела.
, которая удовлетворяла бы дифференциальному уравнению и условиям однозначности, а также определению зависимости количества теплоты от времени для любой точки тела.
Задачи нестационарной теплопроводности решаются как точными аналитическими, так и приближенными методами [7]. При аналитическом способе решение можно представить в виде функциональной зависимости ряда безразмерных комплексов
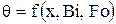 , (1.58)
, (1.58)
где θ - безразмерная температура тела;
Bi - критерий Био, характеризующий связь температурного поля в теле с условиями внешней теплоотдачи;
Fo - критерий Фурье, представляющий собой безразмерное время;
х - безразмерная координата.
 ,
,
где  - характерный размер тела (например, для пластины половина ее толщины, для цилиндра - радиус), м;
- характерный размер тела (например, для пластины половина ее толщины, для цилиндра - радиус), м;
α - коэффициент теплоотдачи на поверхности тела, Вт/м2К;
λ, а - коэффициенты теплопроводности и температуропроводности тела, Вт/(м∙К) и м2/с;
t- время, с.
Выражение (1.58) часто представляется в виде номограмм [5] для тел простейшей геометрической формы (пластина, цилиндр, шар). Номограммы дают зависимость безразмерной температуры в центре и на поверхности тела в зависимости от критериев Био и Фурье при граничных условиях третьего рода и равномерном начальном распределении температуры. Пользуясь этими номограммами можно решать следующие задачи: определять время охлаждения или нагревания до заданной температуры по известным условиям теплоотдачи на поверхности тела; находить температуру в теле через заданное время; определять интенсивность теплоотдачи на поверхностях тела.
Расчет количества теплоты  , отданного или воспринятого телом за время t, производится по выражению
, отданного или воспринятого телом за время t, производится по выражению
 , (1.59)
, (1.59)
где 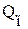 - количество теплоты, которое отдает или воспринимает поверхность тела;
- количество теплоты, которое отдает или воспринимает поверхность тела;
 - средняя безразмерная температура.
- средняя безразмерная температура.
Количество теплоты 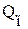 для пластины относят к 1 м2 ее поверхности, а для цилиндра - к 1 м его длины.
для пластины относят к 1 м2 ее поверхности, а для цилиндра - к 1 м его длины.
Тогда в выражении (1.59) величина 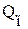 для пластины имеет вид:
для пластины имеет вид:
 ,
,
где δ - толщина пластины;
ρ, с - плотность и теплоемкость материала пластины, а для цилиндра
 ,
,
где  - радиус цилиндра.
- радиус цилиндра.
Более детально ознакомится с рассмотрением аналитического и приближенного методов решения задач нестационарной теплопроводности можно в приводимом списке учебной литературы [7].
Вопросы для самопроверки
1. Сформулируйте основной закон теплопроводности.
2. Дайте характеристику дифференциального уравнения теплопроводности и условий однозначности.
3. Как распределяется температура по толщине плоской и цилиндрической стенок?
4. Сформулируйте условие выбора толщины изоляционного покрытия трубопроводов.
5. Как распределяется температура в пластине с внутренними источниками теплоты?
6. Укажите основные способы интенсификации процессов теплопередачи.
7. Сформулируйте физический смысл коэффициента теплопередачи.
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН (ТЕПЛООТДАЧА)
2.1. Основные понятия и определения
Конвективный теплообмен представляет собой сложный процесс, при котором теплота передается за счет перемещения объемов жидкости (газа) и одновременно за счет теплопроводности между неравномерно нагретыми частицами жидкости. Причиной конвективного теплообмена является неравномерность температурного поля внутри жидкой или газообразной среды (теплоносителя). Математический анализ конвективного теплообмена чрезвычайно сложен [1, 2].
Теплоотдача, характеризующая конвективный теплообмен между потоком движущейся жидкости (газа) и поверхностью, омываемого ею тела, является одним из определяющих факторов в процессах работы энергетического оборудования.
Практические расчеты теплоотдачи основываются на законе Ньютона-Рихмана, полученном на основании обобщения опытных данных. Согласно этого закона полный тепловой поток Q, Вт, отдаваемый в процессе теплоотдачи, пропорционален поверхности теплообмена F и разности температур (температурному напору) поверхности тела  и омывающей ее среды
и омывающей ее среды  :
:
 , (2.1)
, (2.1)
где α - коэффициент пропорциональности, характеризующий интенсивность процесса, получил название коэффициента теплоотдачи.
Коэффициент теплоотдачи α, Вт/(м2∙К), это количество теплоты, которое в единицу времени отдается единицей поверхности тела при разности температур поверхности тела и омывающей среды в один градус.
 . (2.1а)
. (2.1а)
Разность температур в соотношении (2.1) берут по абсолютной величине с учетом, что теплота распространяется самопроизвольно в сторону убывания температуры.
Величина коэффициента теплоотдачи a сложным образом зависит от многих факторов: природы и режима движения, теплофизических свойств жидкости, температуры, формы и размеров поверхности теплообмена, ее положения в пространстве и др. Он не является транспортным свойством подобно коэффициенту теплопроводности, который обычно определяется по таблицам, приводимым в теплотехнических справочниках и пособиях.
По природе возникновения различают свободное (естественное) и вынужденное движение жидкости. Вынужденное движение создается внешними источниками (насосом, вентилятором и др.); свободное движение возникает за счет разности плотности нагретых и холодных слоев жидкости, т.е. под действием архимедовых сил.
Режим движения жидкости играет решающее значение в процессах теплоотдачи, так как определяет физический механизм переноса теплоты. Различают два характерных режима движения - ламинарный и турбулентный. При ламинарном режиме частицы жидкости движутся по упорядоченным траекториям, вид которых определяется формой границ тела. Перенос теплоты осуществляется за счет соприкосновения частиц, слоев жидкости, т.е. за счет теплопроводности. В турбулентном режиме частицы жидкости движутся по случайным траекториям, быстро меняющимся во времени, перенос теплоты происходит в основном за счет интенсивного перемещения частиц жидкости, т.е. за счет конвекции.
У самой поверхности тела из-за наличия вязкого трения скорость движения жидкости падает до нуля. Слой жидкости у поверхности теплообмена, в котором сохраняется ламинарное движение, называется пограничным. Теплота внутри этого слоя переносится теплопроводностью и его можно условно представить как дополнительный изолирующий слой толщиной  между стенкой и ядром потока. Внутри турбулентного ядра потока перенос теплоты осуществляется конвекцией при интенсивном перемещении частиц жидкости. Поскольку интенсивность конвективного теплопереноса существенно выше теплопроводности, то ламинарный слой оказывает основное термическое сопротивление переносу теплоты и в нем происходит наибольшее изменение температуры.
между стенкой и ядром потока. Внутри турбулентного ядра потока перенос теплоты осуществляется конвекцией при интенсивном перемещении частиц жидкости. Поскольку интенсивность конвективного теплопереноса существенно выше теплопроводности, то ламинарный слой оказывает основное термическое сопротивление переносу теплоты и в нем происходит наибольшее изменение температуры.
Из многообразия физических свойств жидкости наибольшее влияние на процесс теплоотдачи оказывают следующие параметры: плотность  , кинематическая вязкость
, кинематическая вязкость  , коэффициент теплопроводности
, коэффициент теплопроводности  , температуропроводность
, температуропроводность  , теплоемкость
, теплоемкость  .
.
Коэффициент теплоотдачи также зависит от геометрических размеров, формы и положения тела.
Все вышеизложенное показывает, что сложность расчета конвективного теплообмена заключается в определении коэффициента т