Исходные данные
Арифметический вариационный факторный признак
Таблица 1
| № | Результативный признак | Факторные признаки | ||
| № 3 (товарная продукция лесозаготовок, тыс. руб) | № 5 (вывозка древесины, лесоматер. Кругл, тыс. м) | № 24 (выработка товарной продукции на 1 работающего, руб) | № 26 (удельные трудозатраты на лесозаготовках, чел.-дней/ 1000 м) | |
| у | х1 | х2 | х3 | |
х1, х2, х3 - независимая переменная (факторный признак)
у - зависимая переменная (результативный признак)
Проверка однородности исследуемой совокупности
В таблице 2 проранжируем исходные данные по результативному признаку (у).
Таблица 2. Ранжированные исходные данные
| № | Результативный признак | Факторные признаки | ||
| № 3 | № 5 | № 24 | № 26 | |
| у | х1 | х2 | х3 | |
у = 11700 - испытуемый элемент совокупности.
Таблица 3. Расчет параметров для проверки однородности исследуемой совокупности
| № | уi | 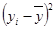
|
| 10562500,00 | ||
| 6002500,00 | ||
| 5062500,00 | ||
| 1102500,00 | ||
| 722500,00 | ||
| 422500,00 | ||
| 62500,00 | ||
| 2500,00 | ||
| 562500,00 | ||
| 902500,00 | ||
| 1322500,00 | ||
| 4622500,00 | ||
| 7022500,00 | ||
| 9922500,00 | ||
| Сумма | 48295000,00 |
Определим среднюю арифметическую вариационного дискретного ряда без испытуемого элемента по формуле:
 =
=  =
=  = 6450
= 6450
Определим дисперсию без учета испытуемого элемента по формуле:
s2 =  =
=  = 3449642,86.
= 3449642,86.
Среднеквадратическое отклонение составит:
s = 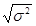 =
= 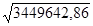 = 1857,32
= 1857,32
Рассчитаем допустимый предел:
D = 4*s = 4*1857,32 = 7429,28
Тогда допустимые границы вариации признака составят:
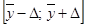 = [6450 - 7429,28; 6450 + 7429,28] = [-979,28; 13879,28].
= [6450 - 7429,28; 6450 + 7429,28] = [-979,28; 13879,28].
Испытуемый элемент у = 11700 входит в расчетные пределы [-979,28; 13879,28]. Соответственно, исследуемая совокупность является однородной и данный элемент не исключается из дальнейшего анализа.
Расчет показателей вариации
Для анализа вариации построим таблицу 4. Данная таблица заполняется на основе таблицы, приведенной в Приложении, и следующих формул:
 =
=  ;
;
s2 =  ;
;
s = 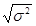 ;
;
Таблица 4. Анализ вариации
| Показатели вариации | y | x1 | x2 | x3 |
 ; ;  6800292,008066,67511,33 6800292,008066,67511,33
| ||||
 ; ; 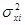 4934666,679922,671352888,696384,89 4934666,679922,671352888,696384,89
| ||||
| sу; sxi | 2221,41 | 99,61 | 1163,14 | 79,91 |
| Vy; Vxi | 32,67 | 34,11 | 14,42 | 15,63 |
Проверка фактического распределения результативного признака на близость к нормальному Проверка проводится по способу Вестергарда, согласно которому фактическое распределение данных можно считать близким к нормальному, если оно удовлетворяет следующим условиям (таблица 5).
Таблица 5
| Если в интервале | Содержится |
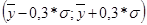 25% 25%
| |
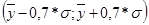 50% 50%
| |
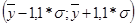 75% 75%
| |
 100% 100%
|
Результаты проверки оформим в таблице 6.
Таблица 6. Проверка на близость к нормальному распределению фактического распределения результативного признака
| Интервалы (числовые данные) | Частота признака при распределении | |||
| Нормальном | Фактическом | |||
| абсолютном | относительном, % | абсолютном | относительном, % | |
| (6134; 7466) | ||||
| (5245; 8355) | ||||
| (4357; 9244) | ||||
| (136; 13464) |
Фактическое распределение результативного признака достаточно близко к нормальному распределению.
Отбор факторных признаков
Основание и отбор факторных признаков можно произвести на основе симметричной матрицы линейных коэффициентов парной корреляции.
Коэффициент парной линейной корреляции можно рассчитать по следующей формуле:
ryxi = 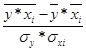 .
.
Результаты представим в таблице 7.
Таблица 7. Симметричная матрица линейных коэффициентов парной корреляции
| у | х1 | х2 | х3 | |
| у | 0,185 | 0,958 | 0,968 | |
| х1 | 0,185 | 0,178 | 0,072 | |
| х2 | 0,958 | 0,178 | 0,964 | |
| х3 | 0,968 | 0,072 | 0,964 |
ryx1 =  = 0,185 - связь слабая, прямая.
= 0,185 - связь слабая, прямая.
ryx2 =  = 0,958 - связь сильная, прямая.
= 0,958 - связь сильная, прямая.
ryx3 =  = 0,968 - связь сильная, прямая.
= 0,968 - связь сильная, прямая.
rx1х2 =  = 0,178 - связь очень слабая, прямая.
= 0,178 - связь очень слабая, прямая.
rx1х3 = 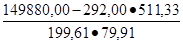 = 0,072 - связь слабая, прямая.
= 0,072 - связь слабая, прямая.
rх2х3 = 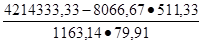 = 0,964 - связи сильная, прямая.
= 0,964 - связи сильная, прямая.
Наиболее тесно связанным результативным признаком является факторный признак х3, поскольку ryx3 = 0,968 - max.
Расчет квадратичной ошибки коэффициента корреляции
Если совокупность относится к однородной и нормально-распределенной, то ошибку коэффициента корреляции можно вычислить по формуле:
hyxi = 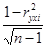 .
.
Результаты расчетов запишем в таблице 8.
Таблица 8. Расчет квадратической ошибки коэффициента корреляции
| ух1х2х3 | ||||
| у | - | 0,176 | 0,022 | 0,017 |
| х1 | 0,176 | - | 0,008 | 0,266 |
| х2 | 0,022 | 0,008 | - | 0,019 |
| х3 | 0,017 | 0,266 | 0,019 | - |
hyx1 =  =(1-0,34225)/3,741657=0,176.
=(1-0,34225)/3,741657=0,176.
hyx2 = 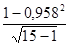 = 0,022.
= 0,022.
hyx3 = 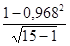 = 0,017.
= 0,017.
hx1х2 = 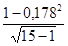 = (1-0,031684)/3,741657=0,008.
= (1-0,031684)/3,741657=0,008.
hx1х3 =  = (1-0,005184)/3,741657=0,266.
= (1-0,005184)/3,741657=0,266.
hx2х3 =  = 0,019.
= 0,019.